探索Transformer在算術問題中的局限性

在近年來的自然語言處理領域，基于Transformer的大型語言模型（LLMs）取得了顯著的成就。然而，當這些模型被應用到看似簡單的算術問題上時，它們常常表現出意外的掙扎，尤其是在處理基本的整數乘法任務時。例如，盡管GPT-4等現代LLM在多種任務中表現出色，但在執行簡單的整數乘法時卻遇到了困難。這種明顯的能力差異引發了人們對于這些模型安全和倫理使用的擔憂，并阻礙了它們的廣泛應用。

本文旨在通過探索和解釋Transformer在整數乘法任務中的不足，來深入理解這些模型在算術問題上的局限性。我們通過對一個標準Transformer模型在n位整數乘法任務中的表現進行全面分析，揭示了模型在處理連續進位和緩存中間結果時的困難，并通過實驗驗證了這些推論。基于這些發現，我們提出了改進措施，以提升Transformer在乘法任務上的性能。這些改進不僅增強了模型的解釋性，還通過嚴格的測試和數學建模得到了驗證，例如，在5位整數乘法任務上，我們實現了超過99.9%的準確率，超過了GPT-4等大型語言模型。

論文標題：Dissecting Multiplication in Transformers: Insights into LLMs

機構：

1. Hong Kong University of Science and Technology
2. Hong Kong Polytechnic University

論文鏈接：??https://arxiv.org/pdf/2407.15360.pdf??

通過本研究，我們不僅提升了對Transformer模型在處理復雜算術任務中的理解，也為AI的安全性和可靠性研究提供了新的視角和方法論，推動了可解釋AI（XAI）的發展，幫助構建了對大型語言模型的信任，并促進了它們在關鍵應用中的采用。

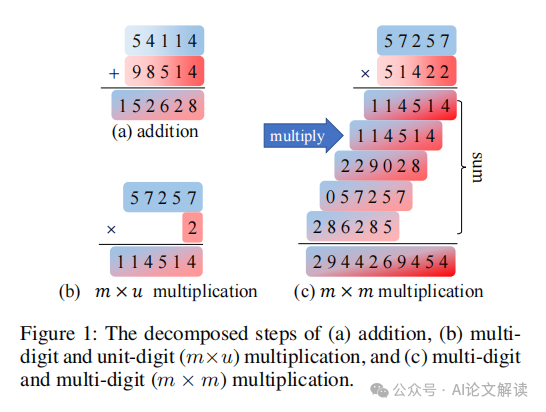
Transformer模型在算術任務中的表現

Transformer模型在自然語言處理任務中取得了顯著的成就，但在算術任務，尤其是整數乘法方面，它們的表現卻常常不盡人意。盡管Transformer擁有龐大的模型能力，它在處理簡單的整數乘法任務時卻表現出明顯的挑戰。這種能力的不對等引起了人們對其安全和道德使用的關注，并阻礙了其廣泛的應用。

在本文中，我們專注于整數乘法任務，探索和解釋Transformer在這一領域的不完美表現。我們對一個基本的Transformer模型進行了全面分析，該模型被訓練用于執行n位整數乘法。我們的觀察表明，模型將乘法任務分解為多個并行的子任務，每個子任務針對每個數字順序優化，以完成最終的乘法計算。

基礎乘法分析：單位數乘法

在對Transformer在m×u（多位數乘以單位數）乘法任務的表現進行分析時，我們發現Transformer利用幾個基本子任務來完成乘法計算。這些子任務包括：

基本乘法（BM）：BM計算兩個單個數字在每個位置的乘積。根據是否產生進位到下一個位置，BM可以分為BM（帶進位）和BM（不帶進位）。

使用進位（UC）：UC考慮前一個數字的進位，并將進位加到當前位置的乘積上。

基于上述基本子任務，Transformer可以將多個子任務鏈接在一起，實現復雜的功能，例如使用進位和進一步進位（UCFC），考慮來自前一列的進位，并進一步產生到下一列的進位。

總體分析

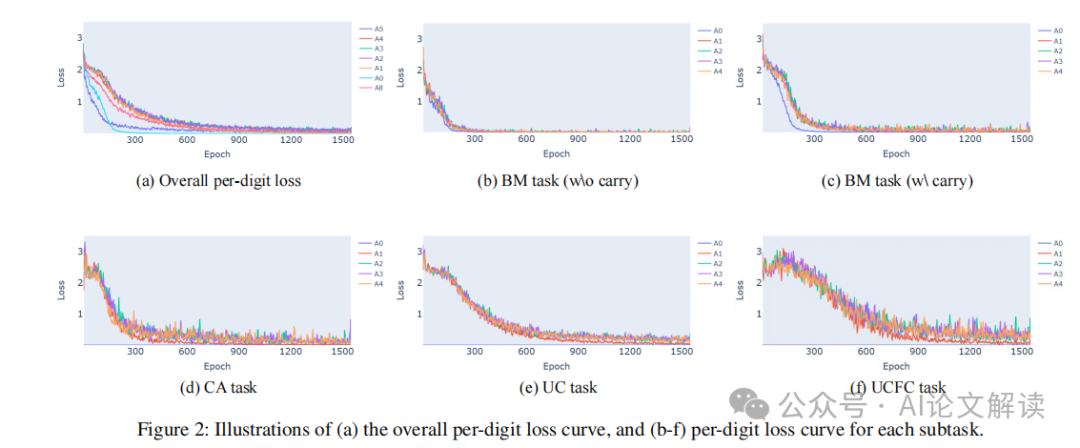
我們首先調查Transformer如何學習每個子任務。通過觀察每個數字的訓練損失，我們發現Transformer似乎是半獨立地學習每個答案數字的。單位數字（A0）和最高位數字（A5）的學習速度比其他數字快，且噪聲更少。這是因為A0的計算不需要考慮進位，從而簡化了計算過程。與A0相比，A5的計算只需要考慮進位。

每個任務的分析

我們進一步分析每個子任務的訓練數據，將訓練數據分為與每個子任務對應的不重疊子集，并分別展示每個子任務的每個數字的損失曲線。從BM（不帶進位）和BM（帶進位）的訓練曲線可以看出，所有任務開始時損失都很高。隨著訓練的進行，所有損失曲線都有所下降，但不同任務之間存在“時間滯后”。BM（不帶進位）的損失下降最快，這是因為它是所有其他任務的基礎，必須先準確計算才能進行后續計算。BM（帶進位）和進位損失的下降速度是第二快的，這兩個子任務是互補的計算，它們的收斂表明模型能夠準確計算進位。UC的損失在訓練初期表現出顯著的平臺期，這符合我們的預期，即UC子任務需要準確計算進位，因此UC的損失只有在進位任務收斂后才能下降。UCFC的損失下降最晚，因為UCFC的計算跨越3個數字，即當前數字的乘積、前一個數字的進位和向下一個數字的進位，因此其收斂發生在所有其他損失收斂之后。

從這些分析中，我們可以看出，盡管Transformer在處理簡單的單位數乘法任務時表現出一定的能力，但在更復雜的多位數乘法任務中，其性能急劇下降，顯示出明顯的不足。這些發現為理解和改進Transformer模型在算術任務中的表現提供了寶貴的見解。

多位數乘法的深入分析

在探討多位數乘法的處理中，我們發現轉換器（transformer）在執行這一任務時會將其分解為多個子任務，并行計算。這些子任務包括基本的數字乘法（Base Multiply, BM），使用進位（Use Carry, UC），以及進一步的進位處理（Further Carry, UCFC）。通過對這些子任務的深入分析，我們可以更好地理解轉換器在處理多位數乘法時的行為模式及其局限性。

基本乘法和進位處理

在多位數乘法中，轉換器首先處理基本的數字乘法，即單個數字間的乘法。這一步驟相對簡單，但關鍵在于如何處理和傳遞進位。例如，在乘法??47134 × 9??中，每一位數字與9相乘后的結果需要考慮前一位的進位，這增加了計算的復雜性。轉換器在這一過程中展示了分階段學習的特點，即先學習無需進位的乘法，然后逐漸學習如何處理進位。

子任務的學習順序

通過觀察損失曲線，我們發現轉換器在學習各個子任務時存在順序性。基本的乘法（BM）通常是最先被學習的，因為它是其他計算的基礎。隨后，轉換器學習如何處理進位（UC），最后是更復雜的進位傳遞（UCFC）。這種學習順序反映了任務的內在復雜性和依賴關系。

提出改進措施

基于上述分析，我們提出以下幾點改進措施，以增強轉換器在多位數乘法任務上的表現：

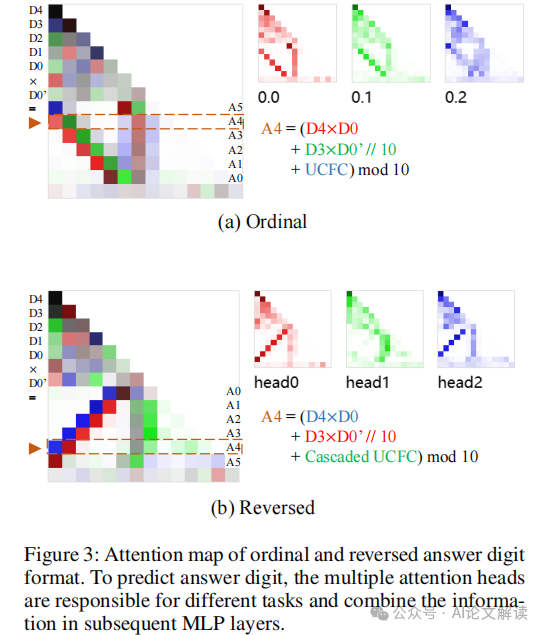
1. 反轉答案數字

研究表明，將答案數字反轉（即從低位到高位進行計算）可以顯著提高模型的準確率。這種方法模仿了人類計算乘法的習慣，從而使得模型能夠更有效地利用已生成的低位數字來預測高位數字。

2. 增加模型深度

多位數乘法涉及復雜的中間步驟和多層次的計算，增加模型的深度可以提供更多的層次來處理這些中間結果，從而提高準確性。實驗表明，增加深度能夠顯著提升模型在處理多位數乘法時的表現。

3. 增加簡單樣本的比例

在訓練初期增加簡單樣本（如單一位數乘法）的比例，可以幫助模型在學習更復雜的多位數乘法前，先掌握基本的乘法規則。這種漸進式學習策略可以減少學習難度，提高模型的整體性能。

通過實施這些改進措施，我們能夠顯著提高轉換器在多位數乘法任務上的準確率和效率，從而推動其在更廣泛的應用場景中的部署和使用。

實驗驗證與結果分析

1. 實驗設計與方法

本研究通過實驗驗證了Transformer在整數乘法任務上的性能。我們首先使用單層解碼器僅Transformer模型在m × u（多位數乘以單位數）乘法任務上進行訓練，并逐步擴展到多層Transformer模型在m × m（多位數乘以多位數）乘法任務上的訓練。實驗中，每個數字在訓練數據中獨立采樣自均勻分布{0,1,...,9}。我們使用Adam優化器，學習率設置為1e-4。

2. 實驗結果

實驗結果顯示，在m × u乘法任務上，Transformer模型能夠通過學習不同的子任務（如基礎乘法、使用進位等）逐步提高預測的準確性。然而，在擴展到更復雜的m × m乘法任務時，模型的準確率顯著下降。這表明單層Transformer模型在處理包含多個中間步驟的復雜任務時存在局限性。

3. 結果分析

通過對不同子任務的訓練損失進行分析（如圖2所示），我們觀察到不同子任務的學習速度存在顯著差異。基礎乘法（BM）任務的損失下降最快，而涉及多個計算步驟的子任務（如使用進位和進一步進位的計算）的損失下降較慢。這些觀察結果支持了我們的假設，即Transformer在處理復雜的算術任務時，其性能受限于對中間計算結果的處理能力。

本文轉載自???AI論文解讀??