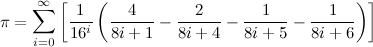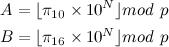算法題:如何判斷計算的 π 值是否精確?
查看下文之前,大家可以先想想。來看看 π 值計算世界紀錄保持者 Mysticial 的回復。
問題(來自Ishan Sharma):
我曾試過用各種不同的方法,來做一個按序輸出顯示 π 值的程序。我試過泰勒級數(shù)法,但是它收斂地非常慢(這是之后,當我將我的結果和網(wǎng)上的值對比時發(fā)現(xiàn)的)。總之,我正試著找出更好的算法。
所以,當我在寫這個程序時總遇到問題,不管使用什么算法,我都有一個困惑:我如何才能知道我計算的數(shù)字是正確的呢?
最高票數(shù)的回答(來自Mysticial):
由于我是計算 π 值的世界紀錄保持者(10 萬億位),我來談一下我的拙見:
除非你是想創(chuàng)造一個新的世界記錄,否則通常的解決辦法就是對比已知值驗證計算值。所以,這很簡單。
其實,我就有一個列出了數(shù)字片段的網(wǎng)頁。它就是為了驗證計算值。http://www.numberworld.org/digits/Pi/
但是,當你進入世界記錄的范圍,就沒有已知值讓你對比驗證了。
通常,驗證計算值的標準方法是用另一種算法再計算一次。所以,只要有一個計算錯誤,數(shù)字就不會相同。
這經(jīng)常會花兩倍多的時間(因為第二種算法一般會慢一點)。但這是驗證計算值的唯一方法,只要你涉及了從沒被計算過的未知領域或是一個新的世界記錄,就只能這么做。
在超級計算機保持世界記錄的時候,有兩種不同的常見AGM算法:
它們都是時間復雜度為 O(N log(N)^2) 的算法,而且相當簡單。但是,如今的算法有些不同了。在最近的3個世界記錄中,我們只通過最快的公式(Chudnovsky 公式)進行一次運算,而不是兩次。
這個算法比較難,但是它比AGM算法快很多。
然后我們用BBP公式進行數(shù)字提取,來驗證這個二進制數(shù)字。
使用這個公式,你可以計算任何二進制數(shù)字,并且不用計算它之前的所有數(shù)字。因此,它用來驗證最后少數(shù)的二進制計算值。所以,它比一個完整的計算要快得多。
它的優(yōu)點是:
1.只需要進行一次復雜的運算。
它的缺點是:
- 需要實現(xiàn)Bailey–Borwein–Plouffe (BBP)公式。
- 需要多一步來驗證:基數(shù)從二進制到十進制的轉換。
我曾列出過一些細節(jié)來說明為什么驗證最后幾個數(shù)字就能證明所有數(shù)字都是正確的。但這是顯而易見的,因為任何計算錯誤都會傳遞到最后一個數(shù)字。
現(xiàn)在,最后一步(驗證轉換)實際上是非常重要的。一位前世界紀錄保持者曾呼吁我們不要這么做,因為,我一開始并沒有給出它詳細的過程。
所以,現(xiàn)在我把我博客的這個片段貼出來:
N = #所需的小數(shù)位數(shù)
p = 64位素數(shù)
用10進制算法計算A,用二進制算法算B。
如果 A=B,那么由于“極大可能性”,轉換是正確的。
深入閱讀,可查看我的這篇博文《Pi – 5 萬億位》。
原文鏈接: Stack Overflow 翻譯: 伯樂在線 - colleen__chen