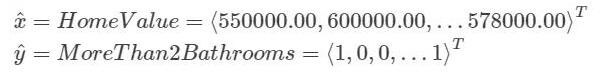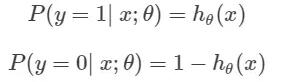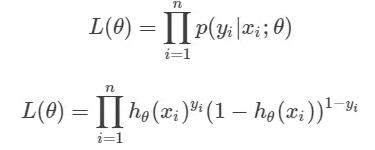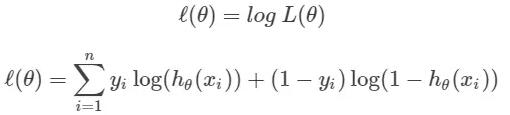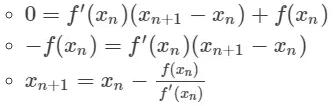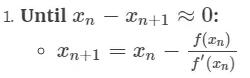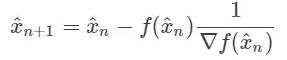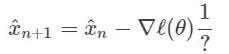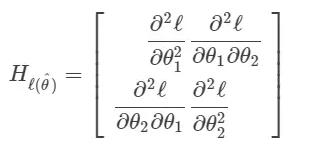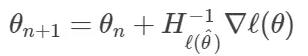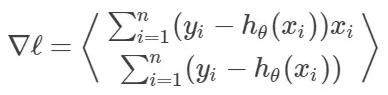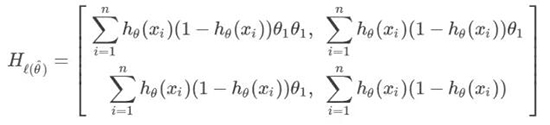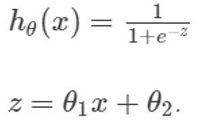如何通過牛頓法解決Logistic回歸問題
本文介紹了牛頓法(Newton's Method),以及如何用它來解決 logistic 回歸。logistic 回歸引入了伯努利分布(Bernoulli distribution)中的對數似然概念,并涉及到了一個稱作 sigmoid 函數的簡單變換。本文還介紹了海森矩陣(這是一個關于二階偏微分的方陣),并給出了如何將海森矩陣與梯度結合起來實現牛頓法。
與最初的那篇介紹線性回歸和梯度的文章相似,為了理解我們的數學思想是如何轉換成在二元分類問題中的解決方案的實現,我們也會用 Python 語言以一種可視化、數學化的方式來探索牛頓法:如何解決 logistic 回歸問題。
讀者需知的先驗知識:
- 微分和鏈式法則(微積分)
- 偏微分與梯度(多元微積分)
- 基本向量運算(線性代數)
- NumPy 的基本理解
- 獨立概率的基本理解
數據
我們的數據集來自南波士頓的房地產,包括每套房子的價格以及一個表明這套房子是否具有兩個浴室的布爾值。
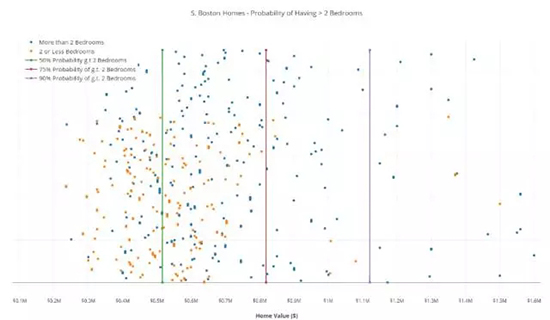
x 是房產價格的向量,y 是房產是否具有兩個浴室的向量
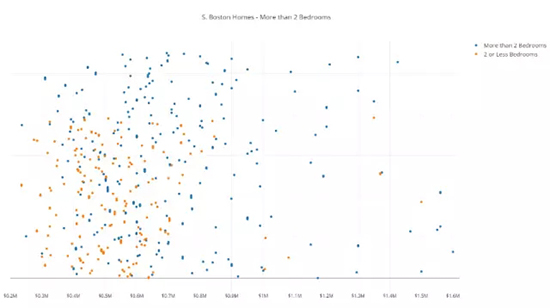
藍色點代表具有兩個以上浴室的房產,橙色點代表具有 2 個或者少于兩個浴室的房產,橫坐標是房產價格。
模型
我們將會學習一個 logistic 回歸模型,它將會作為一個二元分類器來預測一套給定價格(單位是美元)的房產是否具有兩間或者兩間以上的浴室。
我們仍然需要解決一個關于權重和特征的線性組合,但是我們需要結合一個平滑的、而且值域在 [0,1] 之間的函數來對這個線性組合做一個變換(因為我們需要將線性組合與一個二值輸出 0 或者 1 映射起來。)
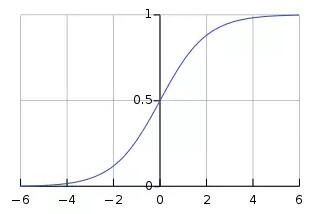
logistic 函數,也就是 sigmoid 函數,能夠完成所有這些事情,函數表達式如下:
注意:為了讓函數具有更多的靈活性,我們在指數項上添加了 θ2 作為一個截距;我們只有一維的數據,即 house_value,但是我們要解決一個二維的模型。
在線性回歸問題中我們定義了我們的平方和目標函數,與這種方法類似,我們想使用假設函數 h(x),并且定義似然函數(likelihood function)來最大化目標函數,擬合出我們的參數。下面是相關內容的數學分析:
數學:定義似然函數
首先,我們要定義一個概率質量函數(Probability Mass Function):
注意:第一個式子中,左側代表得失:在給定的參數 θ 和特征向量 x 的情況下,結果為 1 的概率,我們的假設函數 h_θ(x)來計算這個概率。兩個表達式可以結合成一個,如下所示:
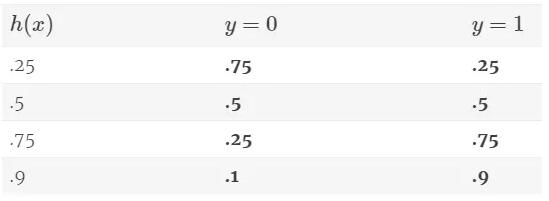
下表展示了使用假設函數得到的錯誤結果是如何通過生成一個較小的值來接受懲罰的(例如,h(x)=.25,y=1h(x)=.25,y=1)。這也有助于理解我們如何把兩個式子合并成一個。
自然而然,我們想把上述正確預測結果的值最大化,這恰好就是我們的似然函數。
我喜歡將似然函數描述成「在給定 y 值,給定對應的特征向量 x^ 的情況下,我們的模型正確地預測結果的似然度。」然而,區分概率和似然值非常重要。
現在我們將似然函數擴展到訓練集中的所有數據上。我們將每一個單獨的似然值乘起來,以得到我們的模型在訓練數據上準確地預測 y 值的似然值的連乘。如下所示:
可以看到我們把 n 個似然值乘了起來(每個似然值都小于 1.0),其中 n 是訓練樣本的數量,我們最后得到的結果的數量級是 10^(-n)。這是不好的一點!最終可能會由于數值太小而用盡計算機的精度,Python 會把特別小的浮點數按照 0 來處理。
我們的解決辦法就是給似然函數取對數,如下所示:
注意:log(x*y) = log(x)+log(y);log(x^n) = n*log(x)。這是我們的假設函數的對數似然值。
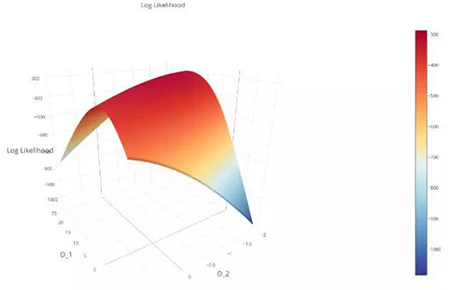
記住,我們的假設函數通過生成一個很小的值來懲罰錯誤的預測,所以我們要將對數似然函數最大化。對數似然函數的曲線如下圖所示:
注意:通過對函數取對數,我們便得到了對數似然值(log-likelihood),我們確保我們的目標函數是嚴格的凸函數(這是一項附加條件),這意味著它有一個全局最大值。
數學:單變量的牛頓法
在我們最大化對數似然函數之前,需要介紹一下牛頓法。
牛頓法是迭代式的方程求解方法;它是用來求解多項式函數的根的方法。在簡單的、單變量的情況下,牛頓法可以通過以下步驟來實現;
求取函數 f(x) 在點 (xn,yn) 處的切線:
求取點 x_n+1, 處的切線的在 x 軸的截距:
求出 x 截距處的 y 值
如果 yn+1−yn≈0:返回 yn+1,因為我們的結果已經收斂了!
否則,更新點 (xn,yn),繼續迭代:
下面的動圖有助于我們可視化這個方法:
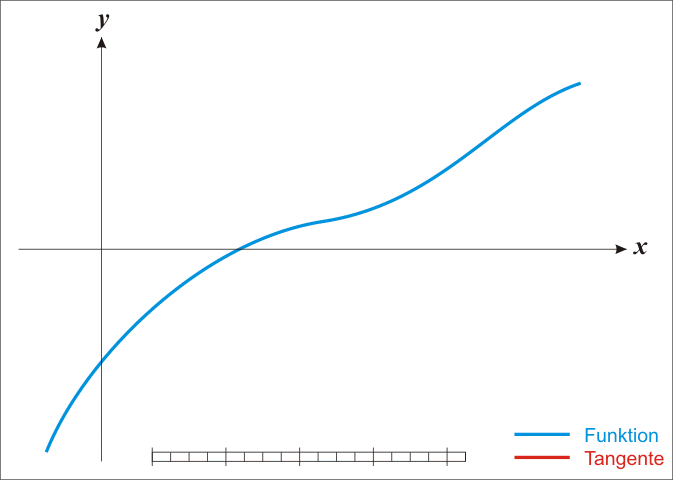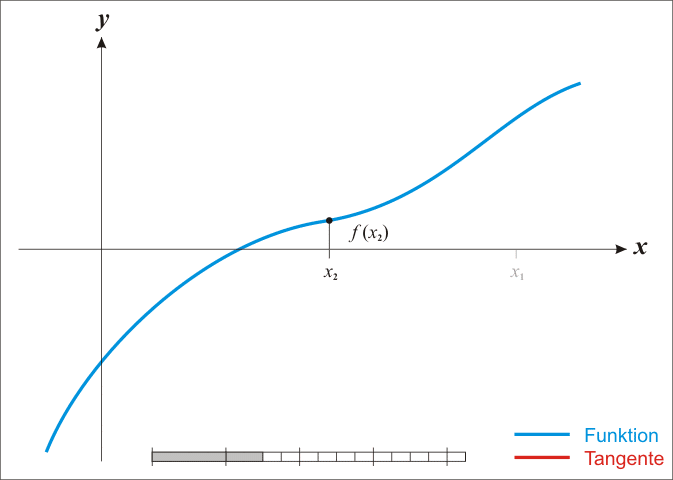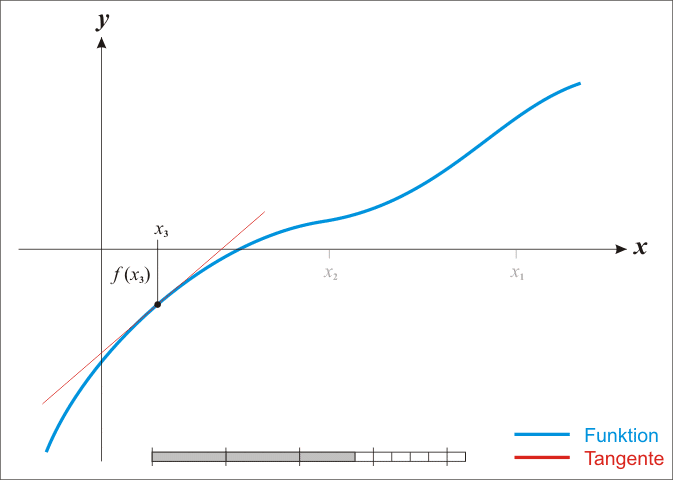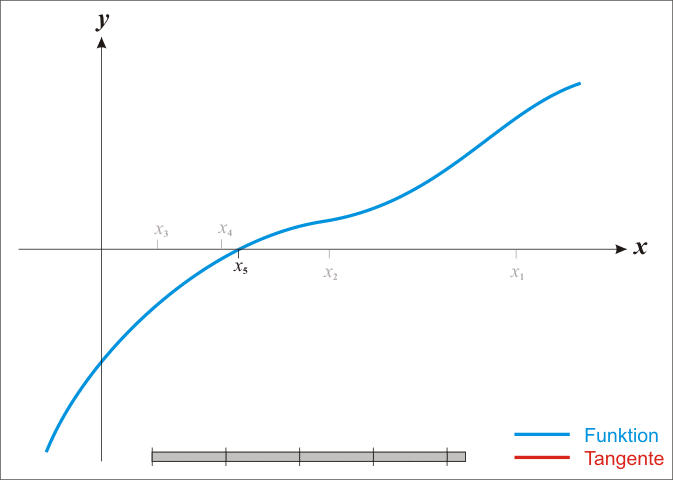
如果你能夠更詳細地理解上述算法,你將看到這個可以歸結為:
任何一位通過高中數學考試的人都能夠理解上面的內容。但是我們如何將其推廣到多變量的「n 維」情況中呢?
數學:N 維問題中的牛頓法
說到 n 維情況,我們用一個叫做梯度的偏微分向量來代替單變量微分。
如果這個概念對你而言有些模糊,那么請復習一下梯度的知識。
所以在多變量的形式中,我們的更新規則變成了參數 x^ 的向量減去 f(x^),如下所示:
注意: f(xn)f′(xn) 中的 f′(xn) 變成了 ∇f(x^n)^(−1),因為我們將標量 f(xn) 推廣到了多變量的情況下,將它變成了梯度的倒數 ∇f(x^n)^(−1)。
數學:用牛頓法最大化對數似然函數
我們要最大化假設函數 hθ(x) 的對數似然值ℓ(θ)。
為了最大化我們的函數,我們要找到函數 f ℓ(θ) 的偏微分,并且將它設為 0,然后從中求出 θ1 和 θ2,來得到微分的臨界點。這個臨界點就是對數似然函數的最大值點。
注意:因為對數似然函數是嚴格的凸函數,所以我們會有一個全局最大值。這意味著我們只有一個臨界點,所以通過上述方法得到的解就是我們的唯一解。
這應該聽起來很熟悉。我們尋求使偏微分為 0 的 θ1 和 θ2。我們找到了梯度向量的根。我們可以使用牛頓法來做這件事!回想一下牛頓法的更新步驟:
我們可以用梯度來代替 f(x^n),這樣就得到了:
那么上面的「?」指的是什么呢?直覺告訴我們,我們需要對梯度向量求導,就像我們之前對 f(x^n) 所做的微分一樣。
開始進入海森矩陣(The Hessian)。
數學:海森矩陣
從關于多元微分的預備知識中可以得知,我們應該知道去求解一個函數的「二階」導數,我們針對每一個參數再給每個一階偏導數求偏導數。如果我們有 n 個參數,那么我們就會有 n^2 個二階偏導數。
結果就是,海森矩陣是一個 n*n 的二階偏導方陣。
在我們的情況中,一共有兩個參數 (θ1,θ2),因此我們的海森矩陣形式如下:
數學:將所有的放在一起
將海森矩陣替換在牛頓法的更新步驟中,我們得到了如下所示的內容:
注意:我們取了海森矩陣的逆矩陣,而不是它的倒數,因為它是一個矩陣。
為了簡單起見,這篇文章省略了對梯度和海森矩陣進行求導的實際過程。要理解后面的求導過程可以參考下面的資源:
1. 我們的對數似然函數的梯度的導數(Derivation of the Gradient of our Log-Likelihood), 吳恩達課程筆記 17-18 頁
2. 海森矩陣的求解其實相當直接,如果你曾經計算過梯度,你會在吳恩達課件筆記中「對 sigmoid 函數求導 g′(z)」那一部分看到。
ℓ(θ) 的梯度是:
ℓ(θ) 的海森矩陣是:
其中:
實現牛頓法
我們從定義假設函數開始,它就是 sigmoid 函數:
- def sigmoid(x, Θ_1, Θ_2):
- z = (Θ_1*x + Θ_2).astype("float_")
- return 1.0 / (1.0 + np.exp(-z))
然后定義我們的對數似然函數 ℓ(θ):
- def log_likelihood(x, y, Θ_1, Θ_2):
- sigmoidsigmoid_probs = sigmoid(x, Θ_1, Θ_2)
- return np.sum(y * np.log(sigmoid_probs)
- + (1 - y) * np.log(1 - sigmoid_probs
最后,我們實現對對數似然函數的梯度求解和海森矩陣求解:
- def gradient(x, y, Θ_1, Θ_2):
- sigmoidsigmoid_probs = sigmoid(x, Θ_1, Θ_2)
- return np.array([[np.sum((y - sigmoid_probs) * x),
- np.sum((y - sigmoid_probs) * 1)]])
- def hessian(x, y, Θ_1, Θ_2):
- sigmoidsigmoid_probs = sigmoid(x, Θ_1, Θ_2)
- d1 = np.sum((sigmoid_probs * (1 - sigmoid_probs)) * x * x)
- d2 = np.sum((sigmoid_probs * (1 - sigmoid_probs)) * x * 1)
- d3 = np.sum((sigmoid_probs * (1 - sigmoid_probs)) * 1 * 1)
- H = np.array([[d1, d2],[d2, d3]])
- return H
實現了上述 4 個數學過程之后,我們就使用牛頓法創建我們的外部 while 循環,直到結果在最大值的地方達到收斂。
- def newtons_method(x, y):
- """
- :param x (np.array(float)): Vector of Boston House Values in dollars
- :param y (np.array(boolean)): Vector of Bools indicting if house has > 2 bedrooms:
- :returns: np.array of logreg's parameters after convergence, [Θ_1, Θ_2]
- """
- # Initialize log_likelihood & parameters
- Θ_1 = 15.1
- Θ_2 = -.4 # The intercept term
- Δl = np.Infinity
- l = log_likelihood(x, y, Θ_1, Θ_2)
- # Convergence Conditions
- δ = .0000000001
- max_iterations = 15
- i = 0
- while abs(Δl) > δ and i < max_iterations:
- i += 1
- g = gradient(x, y, Θ_1, Θ_2)
- hess = hessian(x, y, Θ_1, Θ_2)
- H_inv = np.linalg.inv(hess)
- # @ is syntactic sugar for np.dot(H_inv, g.T)¹
- Δ = H_inv @ g.T
- ΔΘ_1 = Δ[0][0]
- ΔΘ_2 = Δ[1][0]
- # Perform our update step
- Θ_1 += ΔΘ_1
- Θ_2 += ΔΘ_2
- # Update the log-likelihood at each iteration
- l_new = log_likelihood(x, y, Θ_1, Θ_2)
- Δll = l - l_new
- l = l_new
- return np.array([Θ_1, Θ_2])
可視化牛頓法
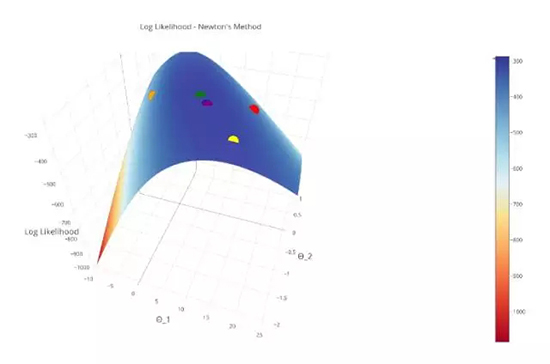
讓我們看一下當我們把在對數似然曲面上使用牛頓法的每一次迭代都畫出來的時候會發生什么?
注意:第一次迭代是紅色的,第二次是橙色的...... 最后一次迭代是紫色的。
在這幅圖中,可以確認我們的「紫色區就是最大值」,我們成功地收斂了!
可視化我們的解
通常,為了可視化一個 1 維數據集,你會把所有的點在數字軸上畫出來,并在數字軸的某處設置一個界限。然而這里的問題是所有的數據點都被混在一起了。
所以,我們在 x 軸將它們展開,并將這些點用顏色來標記。我們也畫出了 3 條界線來區分房產的百分比——正如圖例解釋的一樣。
結論
我們介紹了一些新主題,包括海森矩陣、對數似然以及 sigmoid 函數。將這些方法結合在一起,我們就能實現用牛頓法來解決 logistic 回歸問題。
盡管這些概念促使形成了實現我們的解決方案的具體化的基礎,但是我們仍然需要注意那些能夠導致牛頓法發散的地方,這些內容超出了本文所要討論的范圍,但是你可以閱讀更多發散資料。
原文:
http://thelaziestprogrammer.com/sharrington/math-of-machine-learning/solving-logreg-newtons-method
【本文是51CTO專欄機構“機器之心”的原創譯文,微信公眾號“機器之心( id: almosthuman2014)”】