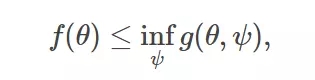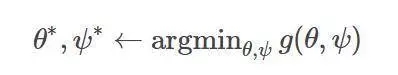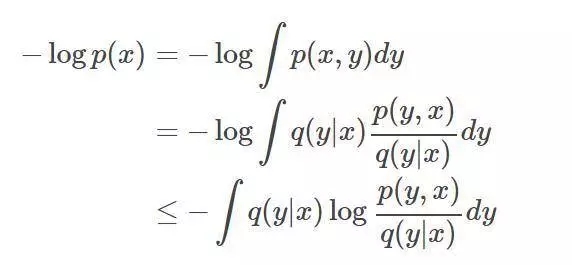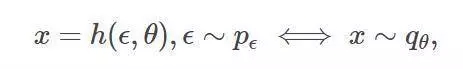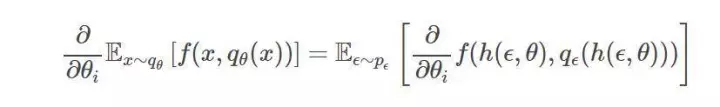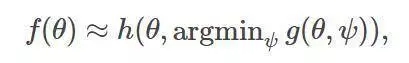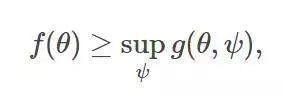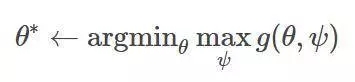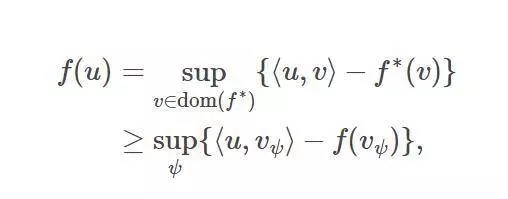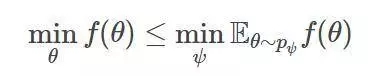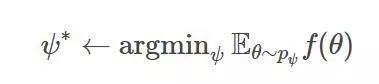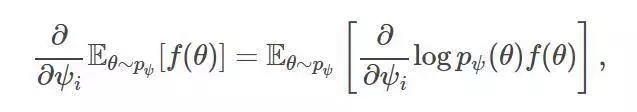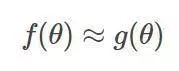[[210651]]

年薪十萬？對于程序員來說，這僅僅是溫飽水平。

根據國家統計局今年上半年發布的消息，2016 年信息傳輸、軟件和信息技術服務業的平均工資為 122478 元，首次打敗金融業成為新霸主，是全國城鎮單位就業人員平均水平 57394 元的兩倍以上。

然后 AI 浪潮來臨，已經率先脫貧的程序員群體又迎來了升職加薪好時機：轉型AI工程師。

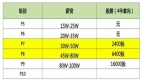
AI科技大本營發現，目前互聯網企業招聘的名單里面 41% 是和 AI 跟算法相關的，并且由于人才奇缺，公司開出的薪資也非常的高。在 2018 年高校校招開出的薪資中，Google 是最高的，有 56 萬。另外，我們統計社招平均的月薪中可以看到跟 AI 相關的，基本都四萬以上了。

小康變中產，只差臨門一腳了。

為此，營長特意為轉型過程中的AI工程師們準備了一道大餐——機器學習進階手冊，它是Reddit機器學習論壇上周周榜的第一。

這篇文章是Twitter機器學習專家Ferenc Huszár關于轉換算法的一系列經驗之談，他在Twitter Cortex機器學習團隊專門研究視覺數據的非監督學習。文章內容不是面向機器學習新手的入門介紹，而是關于VAE、GAN、強化學習等話題的一系列研究技巧。

下面是他所寫的具體內容，只要你讀懂了，你肯定就會比營長更加接近西二旗碼農程們那月薪5萬的高端生活。（營長正在默默地求高中老師能重新教一回那些最簡單的概率、統計。）

本周忙得要死，沒讀任何新東西，所以只能分享一些我為自己所寫的機器學習技巧，內容是關于機器學習的各種變換算法。通過這些變換，你就能把眼前的機器學習問題轉化成我們已知的、能夠解決的問題——即找出易處理的向量場量內的穩定“吸引子”（譯注：“吸引子”，Attractors，是指一個系統行為的歸宿或被吸引到的地方）。

典型的情況是這樣的：你有一些模型參數，比如θ。你想優化其中的某些客觀標準，可使用下列方法來優化問題又相當棘手。所以你要將問題進行轉換，如果轉化之后的問題能被有效優化，你就能解決問題；如果不能優化，你可以在此基礎上繼續轉換，直到問題可以被有效優化為止。

更新：雖說我寫的時候稱此為參考手冊，但正如眼尖的Reddit讀者所評論的，本文在內容上并未做到面面俱到，作為參考手冊太勉強了。這里不妨視之為機器學習研究的某種示范操作，就像編譯器一樣，將抽象的機器學習問題編譯成尋找易處理向量場中穩定吸引子的優化問題。

作為首批示范，我先介紹下列問題的轉換：

• 變分不等式
• 對抗博弈
• 進化策略
• 凸松弛

其他轉換還包括對偶原理、半二次分裂、拉格朗日乘子，等等。對于你希望談論的話題，歡迎在評論區寫出來，下次我會補上這些內容。

變化不等式

典型問題：

我的損失函數 f(θ) 很難計算，主要是它涉及到難以解決的邊緣化問題。我無法評估它，只能將其最小化。

解決方法：

讓我們構建一組典型的可微分的上邊界：

以解決最優化問題：

嚴格來講，一旦優化完成，你就可以丟棄輔助參數ψ∗——盡管事實通常表明，參數本身還是很有意義的，如在VAE的識別模型里面用作近似推斷。

轉換技巧：

Jensen不等式：凸函數的平均值絕不會低于用來擬合平均值的凸函數取值。

通常以標準ELBO（evidence lower bound）變體的形式出現，求導如下：

再參數化竅門：在變分推斷中，我們往往會遇到如下形式的梯度：

其中，變量的概率分布函數（ probability distribution function）以積的形式呈現。如果我們能找到一個函數

，

并且該函數處處可微。它的第二個參數，以及參數參數pε對ε的概率分布，則易于通過采樣所獲，如下所示：

然后我們就能使用下面這個在變分上界常常都會用到的積分重構：

相比于強化估計（REINFORCE estimators），使用蒙特卡洛估計來計算期望，往往能得出更小的方差。

對抗博弈

典型問題：

我無法從樣本中直接估計損失函數f(θ)，通常因為損失函數取決于模型或數據分布的概率分布函數（ probability distribution function），或兩者皆有。

解決方法：

我們可以構造出某種近似，令

而后，我們就能解決雙人博弈問題中的穩定均衡，令雙方分別最小化有關于ψ的損失函數g和有關θ的損失函數h。

在h=-g的情況下，該近似表達式則表現為變分下界的形式：

此時，我們可以轉而用以下的極大極小值問題來代替：

變換竅門：

輔助任務中的貝葉斯優化：當損失函數取決于易采樣樣本的概率分布密度時，可以構造一個輔助任務，而輔助任務的貝葉斯優化解決方案取決于密度的值。這類輔助任務的例子有極大似然估計的二進制分類、估計分數函數的去噪或分數匹配。

凸共軛：在損失函數包含密度凸函數（如f-divergences中）的情況下，你能夠通過依照凸共軛的形式來重新表述，以轉換問題。f的凸共軛f*則可表達成：

其中，如果u是一個密度函數，那么內積⟨u,v_ψ⟩就是v_ψ的期望，這就能用蒙特卡羅近似采樣。

進化策略

典型問題：

我的損失函數f(θ)易于評估，但卻難以優化，可能是因為它包含了離散運算，或是該函數為分段型常量函數，無法進行反向傳播。

解決方法：

對于任意概率分布pψ，它在θ上的函數值都滿足于：

因而，使用進化策略，我們可專注于下列問題來做優化：

通常，由于依賴于函數f和概率分布pψ的類型，f的局部最小值能夠從ψ的局部最小值中恢復。

轉換竅門：

強化梯度估計：依賴于下述技巧：

其中，RHS可以用蒙特卡洛輕松近似。蒙特卡洛強化估計的方差往往相對較高。

凸松弛

典型問題：

我的損失函數f(θ)難以優化，因為它不可微，且有非凸部分。如稀疏方法向量的ℓ0范數，或分類問題中的單位階躍函數。

解決方法：

用凸近似來代替非凸的部分，將你的目標轉化為一個典型的凸函數g

轉換竅門：

ℓ1損失函數：在一些稀疏的學習情景中，我們希望能最小化某個向量中的非零項，這就是ℓ0損失函數，通常可以用該向量的ℓ1范數來替代其損失函數。

Hinge損失函數與大間隔方法：在0-1損失下，二值分類器的錯誤率目標通常是其參數的分段常值函數，因此難以優化。我們可以用hinge損失函數來代替0-1損失函數，它可被理解為一個凸上界。結果，優化問題將最大化分類器的間隔。

不過，想要真正實現年薪 50 萬，只看營長的文章還遠遠不夠，堅持學習才是真正的利器，望各位讀者共勉。