前段時間和某銀行合作共同開發了適合我們的一套支付系統。最近，我們對賬發現某些訂單始終都對不齊。銀行的下單金額與對賬金額始終少了1分錢。

這就奇怪了，如果這種異常訂單一多就是少了很多錢。在涉及錢的金融領域，這是個很謹慎嚴肅的問題。

我們跟銀行排查發現了問題的原因，也就是我今天想聊的關于技術上的東西：double精度的丟失問題。

1問題復現

我們先舉個簡單的例子

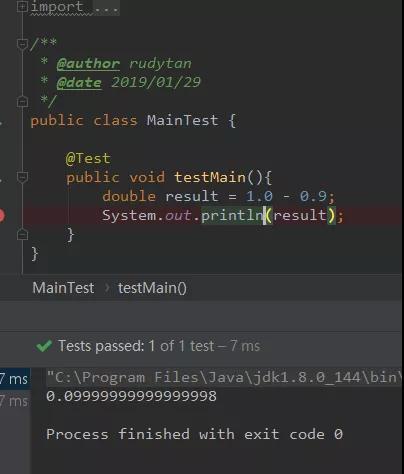
double result = 1.0 - 0.9; 

這段代碼中result等于多少?0.1么?如果執行代碼的話，分分鐘打臉。

double精度丟失問題

2背后原理

無論是我們本文提到的double，還是float，都是浮點數。

在計算機科學中，浮點(英語：floating point，縮寫為FP)是一種對于實數的近似值數值表現法，由一個有效數字(即尾數)加上冪數來表示，通常是乘以某個基數的整數次指數得到。以這種表示法表示的數值，稱為浮點數(floating-point number)。

計算機使用浮點數運算的主因，在于計算機使用二進位制的運算。

例如：4÷2=2，4=100(二進制)、2=010(二進制)。在二進制中除以2相當于退一位數。

那么1.0÷2=0.5=0.1(二進制)也就是1/2，依此類推二進制的0.01(二進制)就是十進制 1/(2^2) = 1/4 = 0.25。

上面看到的1、0.5、0.25那都是可以轉換成二進制的小數，如十進制的0.1，就無法用二進制準確的表示出來。因此只能使用近似值的方式表達。

比如，我們嘗試著把10進制的0.1轉化成二進制試試，步驟如下：

0.1*2＝0.2……0——整數部分為“0”。整數部分“0”清零后為“0”，用“0.2”接著計算。 
0.2*2＝0.4……0——整數部分為“0”。整數部分“0”清零后為“0”，用“0.4”接著計算。 
0.4*2＝0.8……0——整數部分為“0”。整數部分“0”清零后為“0”，用“0.8”接著計算。 
0.8*2＝1.6……1——整數部分為“1”。整數部分“1”清零后為“0”，用“0.6”接著計算。 
0.6*2＝1.2……1——整數部分為“1”。整數部分“1”清零后為“0”，用“0.2”接著計算。 
0.2*2＝0.4……0——整數部分為“0”。整數部分“0”清零后為“0”，用“0.4”接著計算。 
0.4*2＝0.8……0——整數部分為“0”。整數部分“0”清零后為“0”，用“0.8”接著計算。 
0.8*2＝1.6……1——整數部分為“1”。整數部分“1”清零后為“0”，用“0.6”接著計算。 
0.6*2＝1.2……1——整數部分為“1”。整數部分“1”清零后為“0”，用“0.2”接著計算。 
0.2*2＝0.4……0——整數部分為“0”。整數部分“0”清零后為“0”，用“0.4”接著計算。 
0.4*2＝0.8……0——整數部分為“0”。整數部分“0”清零后為“0”，用“0.2”接著計算。 
0.8*2＝1.6……1——整數部分為“1”。整數部分“1”清零后為“0”，用“0.2”接著計算。 
…… 

可以發現，這個過程是除不盡的，除出了一個***循環小數：二進制的 0.0001100110011…

那么，如何在計算機中表示這個***不循環的小數呢?只能考慮按照不同的精度保理不同的位數。

我們知道float是單精度的，double是雙精度的。不同的精度，其實就是保留的有效數字位數不同，保留的位數越多，精度越高。

所以，浮點數在Java中是無法精確表示的，因為大部分浮點數轉換成二進制是一個***不循環的小數，只能通過保留精度的方式進行近似表示。

在《阿里巴巴Java開發手冊》中其實也有著明確的規定，說明了小數類型禁止使用float或者double來表示。(雖然這條是Mysql相關規則，但是Java代碼同樣適用。)

3問題引申

我們現在基本已經知道了double的精度問題是什么問題。

在實際的訂單交易過程中，出現這個問題的更多場景是金額單位元與分的轉換。銀行給你的單位是元，你自己的運算是分;前端輸入是元，計算是分等等。

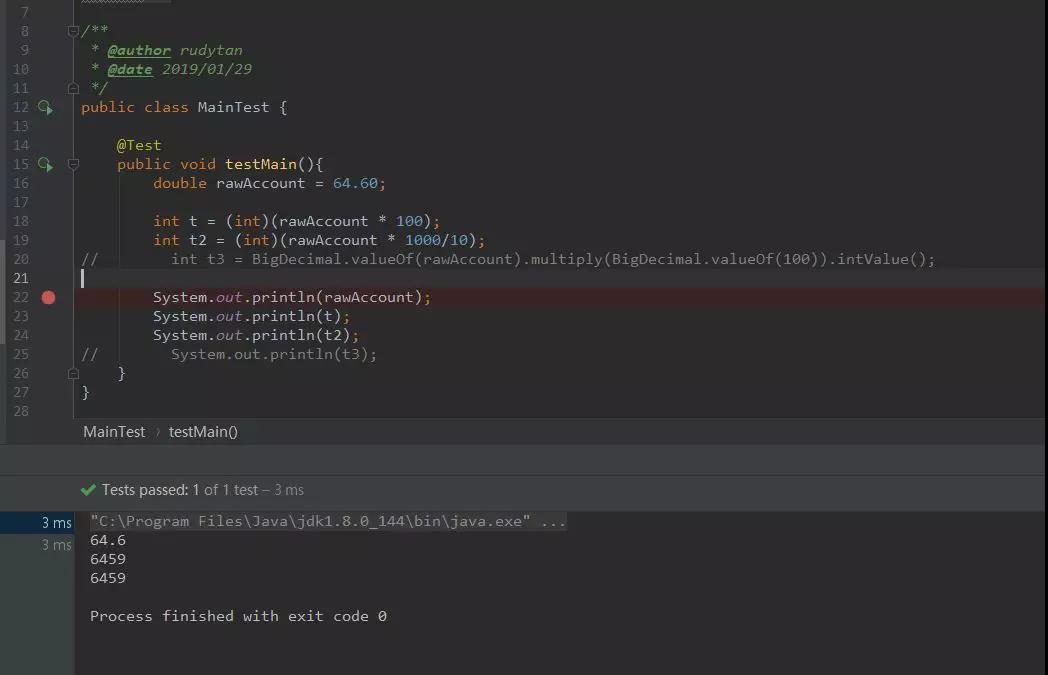
舉個例子：用戶下了一筆64.6元的訂單，你在需要轉換成分。如果直接除以100，你會發現計算出來的分始終是6459，少1分錢。

金額丟失1分問題

4解決方式

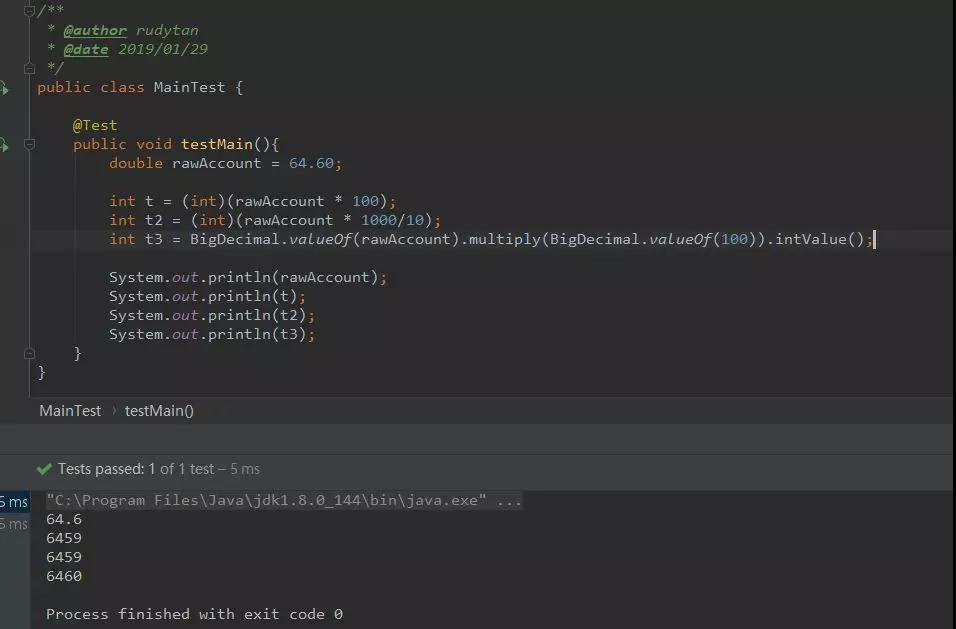
1）使用BigDecimal

為了解決這種浮點小數進度丟失問題，java提供了一種計算方式BigDecimal。

BigDecimal

這樣就可以了么? 不是，這樣能解決大部分問題，假如其他系統或語言不支持BigDecimal呢。當我們無法解決這個問題的時候，我們需要做的是想辦法規避這個問題帶來的影響。

2）以分為單位，Long為數據結構存儲

目前我們某些核心系統在金額傳輸的過程和存儲中還是以元存儲浮點數。導致低于10元的訂單計算利息費率的時候，無法計算清楚，使得我們的業務服務在處理這些問題頭疼死了。

整數與整數的計算，就沒有這些精度丟失問題。Long取值范圍(9223372036854775807)完全夠用。

3）除不盡怎么辦

對于除法，始終會產生除不盡的情況怎么辦?有個詞叫軋差

什么意思呢?舉個簡單例子。假如現在需要把10元分成3分，如果是10除以3這么除，會發現為3.33333無窮盡的3。這些數字完全無法在程序或數據庫中進行精確的存儲。

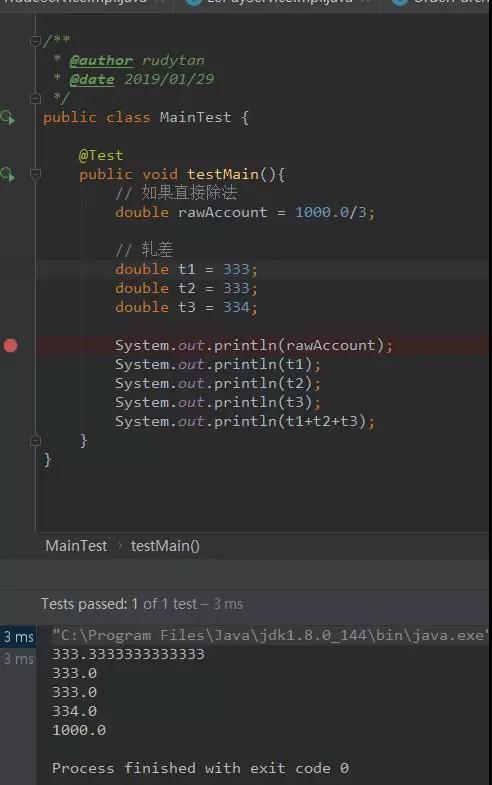
簡單理解就是，當除不盡或需去除小數點的時候，前面的n-1筆(這里n=3)做四舍五入。***一筆做兜底(總金額減去前面n-1筆之和)。這樣保證總金額的不會丟失。

這里我們的具體應用場景是用戶使用了現金券，然后有部分退款，計算應退本金的問題。現金券的處理又是一大篇文章，這里以后有機會再介紹。

5總結能用Long不用浮點數存儲。

前后端傳輸金額(元)的時候，請使用字符串，不要使用浮點數。

浮點數運算請使用BigDecimal。

實在無法除盡，可以考慮通過軋差的方式解決。

double精度不是坑，是個容易忽視的巨坑，小小經驗希望對大家有所幫助，謹慎對待。>-<

關于銀行1分差的問題，等待銀行修復，歷史訂單做調賬處理，哈哈哈哈哈。