掌握套路,你也會用動態規劃
介紹
動態規劃并不是一種具體的算法,而是一種思想,個人覺得就是緩存+枚舉,把求解的問題分成許多階段或者多個子問題,然后按順序求解各子問題。前一子問題的解為后一子問題提供了有用的信息。在求解任一子問題時,列出各種可能的局部解,通過決策保留那些有可能達到最優的局部解,丟棄其他局部解。依次解決各子問題,最后一個子問題就是初始問題的解。
所以動態規劃一般用來求最優解(對子問題進行決策),求種類數(對子問題進行加和)
先分享幾個經典的動態規劃實現,后續再分析幾個面試題
最長上升子序列
來源:LeetCode 300.最長上升子序列
描述:給定一個無序的整數數組,找到其中最長上升子序列的長度。
示例:
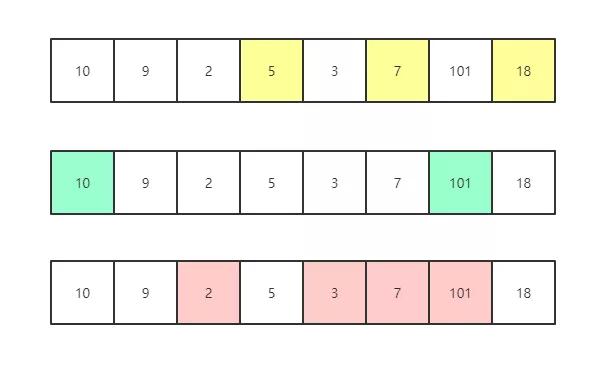
- 輸入: [10,9,2,5,3,7,101,18]
- 輸出: 4
- 解釋: 最長的上升子序列是 [2,3,7,101],它的長度是 4。
可能會有多種最長上升子序列的組合,你只需要輸出對應的長度即可。你算法的時間復雜度應該為 O(n2) 。進階: 你能將算法的時間復雜度降低到 O(n log n) 嗎?
思路:子序列有很多,最長的長度為4
我們假設dp[i]存的是到第i個元素時,數組的最長子序列,則對應的狀態轉移方程為
- dp[i] = max{1, dp[j] + 1 | j < i 且 arr[j] < arr[i]}
其中1為只有自己一個元素,則遞增子序列的長度為1
- public class Solution {
- public int lengthOfLIS(int[] nums) {
- int max = 0;
- int[] dp = new int[nums.length];
- for (int i = 0; i < nums.length; i++) {
- dp[i] = 1;
- for (int j = 0; j < i; j++) {
- if (nums[i] > nums[j] && (dp[j] + 1) > dp[i]) {
- dp[i] = dp[j] + 1;
- }
- }
- if (dp[i] > max) {
- max = dp[i];
- }
- }
- return max;
- }
- }
數塔問題
來源:LeetCode 120. 三角形最小路徑和描述:給定一個三角形,找出自頂向下的最小路徑和。每一步只能移動到下一行中相鄰的結點上。
相鄰的結點 在這里指的是 下標 與 上一層結點下標 相同或者等于 上一層結點下標 + 1 的兩個結點。
例如,給定三角形:
- [
- [2],
- [3,4],
- [6,5,7],
- [4,1,8,3]
- ]
自頂向下的最小路徑和為 11(即,2 + 3 + 5 + 1 = 11) 說明:如果你可以只使用 O(n) 的額外空間(n 為三角形的總行數)來解決這個問題,那么你的算法會很加分。
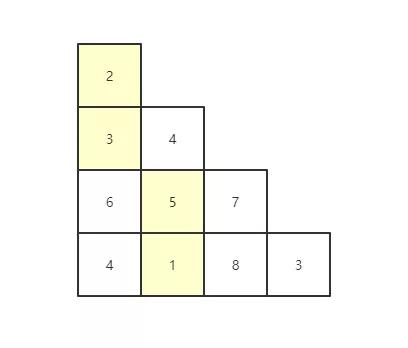
思路:把這個圖形換一下,方便講遞推公式
- [2],
- [3,4],
- [6,5,7],
- [4,1,8,3]
我們可以從底到頂來算最優值。dp[i][j]為從最底部到第i行第j列的最小路徑和,value[i][j]為第i行第j列的值,狀態轉移方程為
- dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]
- public class Solution {
- public int minimumTotal(List<List<Integer>> triangle) {
- if (triangle == null || triangle.size() == 0) {
- return 0;
- }
- // 這里行和列加1,是為了不用處理最下面一行的邊界
- int[][] dp = new int[triangle.size() + 1][triangle.size() + 1];
- for (int i = triangle.size() - 1; i >= 0; i--) {
- List<Integer> rows = triangle.get(i);
- for (int j = 0; j < rows.size(); j++) {
- dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + rows.get(j);
- }
- }
- return dp[0][0];
- }
- }
最長公共子串
來源:LeetCode 1143. 最長公共子序列描述:給定兩個字符串 text1 和 text2,返回這兩個字符串的最長公共子序列的長度。
一個字符串的 子序列 是指這樣一個新的字符串:它是由原字符串在不改變字符的相對順序的情況下刪除某些字符(也可以不刪除任何字符)后組成的新字符串。例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。兩個字符串的「公共子序列」是這兩個字符串所共同擁有的子序列。
若這兩個字符串沒有公共子序列,則返回 0。示例 1:
- 輸入:text1 = "abcde", text2 = "ace"
- 輸出:3
- 解釋:最長公共子序列是 "ace",它的長度為 3。
示例 2:
- 輸入:text1 = "abc", text2 = "abc"
- 輸出:3
- 解釋:最長公共子序列是 "abc",它的長度為 3。
示例 3:
- 輸入:text1 = "abc", text2 = "def"
- 輸出:0
- 解釋:兩個字符串沒有公共子序列,返回 0。
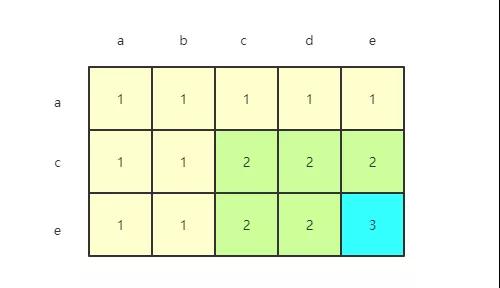
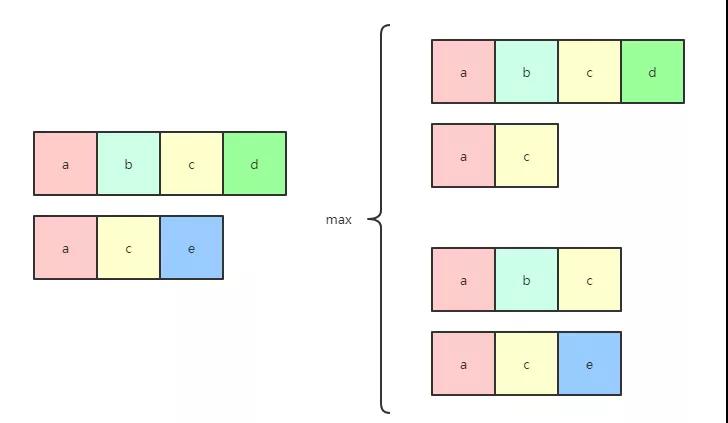
思路:這個題確實比較抽象,上圖
s1=a s2=a,最長公共子串長度為1 s1=ac s2=abc,對應的公共子串長度為2
dp[i][j]為第一個字符串長度為i和第二個字符串長度為j時對應的最長公共子串 狀態轉移方程為
- if(s1.charAt(i) == s2.charAr(j))
- dp[i][j] = dp[i-1][j-1] + 1;
- else
- dp[i][j] = Math.max(dp[i-1][j], dp[i][j -1]);
還是畫圖演示一下遞推公式
- public class Solution {
- public int longestCommonSubsequence(String text1, String text2) {
- if (text1 == null || text2 == null || text1.length() == 0 || text2.length() == 0) {
- return 0;
- }
- int[][] dp = new int[text1.length() + 1][text2.length() + 1];
- for (int i = 1; i <= text1.length(); i++) {
- for (int j = 1; j <= text2.length(); j++) {
- if (text1.charAt(i - 1) == text2.charAt(j - 1))
- dp[i][j] = dp[i - 1][j - 1] + 1;
- else
- dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
- }
- }
- return dp[text1.length()][text2.length()];
- }
- }
背包問題
是男人就看《背包九講》,作為動態規劃的入門課,《背包九講》必不可少。這次就只分享背包九講中最簡單的01背包
來源:藍橋杯
問題描述:給定N個物品,每個物品有一個重量W和一個價值V.你有一個能裝M重量的背包.問怎么裝使得所裝價值最大.每個物品只有一個. 輸入格式 輸入的第一行包含兩個整數n, m,分別表示物品的個數和背包能裝重量。 以后N行每行兩個數Wi和Vi,表示物品的重量和價值 輸出格式 輸出1行,包含一個整數,表示最大價值。樣例輸入 3 5 2 3 3 5 4 7 樣例輸出 8 數據規模和約定 1<=N<=200,M<=5000.
思路:這是最簡單的01背包,都不帶變形的,每種物品僅有一件,可以選擇放或不放。
第i件物品的重量是w[i],價值是v[i] 用dp[i][j]表示前i件物品放入一個承重為j的背包可以獲得的最大價值,狀態轉移方程為
- dp[i][j] = max{dp[i-1][j], dp[i-1][j-w[i]] + c[i]}
即
- dp[i][j] = max{不放第i件物品,放第i件物品}
你可以照著這個狀態轉移方程自己寫一下,我下面這種寫法直接用了滾動數組,把數組從二維變成了一維,節省了空間,有興趣的可以參考其他博客學習這種寫法,本文就不深入了。
- public class Main {
- public static void main(String[] args) {
- Scanner in = new Scanner(System.in);
- int n = in.nextInt();
- int m = in.nextInt();
- int[] widght = new int[210];
- int[] value = new int[210];
- int[] dp = new int[5010];
- for (int i = 0; i < n; ++i) {
- widght[i] = in.nextInt();
- value[i] = in.nextInt();
- }
- for (int i = 0; i < n; ++i) {
- for (int j = m; j >= widght[i]; j--) {
- dp[j] = Math.max(dp[j], dp[j - widght[i]] + value[i]);
- }
- }
- System.out.println(dp[m]);
- }
- }
不同路徑
來源:LeetCode 62不同路徑
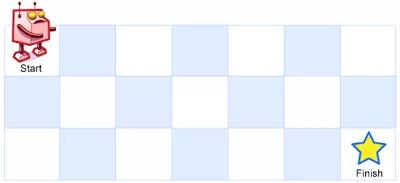
描述:一個機器人位于一個 m x n 網格的左上角 (起始點在下圖中標記為“Start” )。機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角(在下圖中標記為“Finish”)。問總共有多少條不同的路徑?
例如,上圖是一個7 x 3 的網格。有多少可能的路徑?說明:m 和 n 的值均不超過 100。
示例:輸入: m = 3, n = 2,輸出: 3 解釋:從左上角開始,總共有 3 條路徑可以到達右下角。
向右 -> 向右 -> 向下
向右 -> 向下 -> 向右
向下 -> 向右 -> 向右
思路:這個大家一下就會想到用遞歸解決,假設f(m,n)表示移動到點(m,n)的路徑數,因為機器人智能向下或者向右移動,所以點(m,n)只能從點(m-1,n)和(m,n-1)移動而來,遞歸公式就是f(m,n)=f(m-1,n)+f(m,n-1),遞歸的出口呢?當然就是網格的邊界了,網格邊界上的點都只有一種方法,按照這種思路寫出來如下代碼
- class Solution {
- public int uniquePaths(int m, int n) {
- // 在網格邊界的格子只能有一種走法
- if (m == 1 || n == 1) {
- return 1;
- }
- // m,n這個位置只能從(m - 1 , n)和(m, n - 1)移動而來
- return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
- }
- }
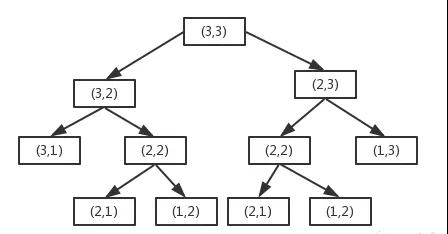
其實這個代碼效率還是很低的,因為有很多重復的計算,如下圖
當m和n為(3,3)時,(2,2)被計算了2次,而且m和n越大,重復計算的次數最多,我們可以把已經算出來的值保存一下,這樣下次再用的時候就不用算了,直接取就行,叫做備忘錄算法,grid[m][n]表示走到(m,n)這個點時的路徑數。
- class Solution {
- public static int[][] grid = new int[110][110];
- public int uniquePaths(int m, int n) {
- if (grid[m][n] != 0)
- return grid[m][n];
- if (m == 1 || n == 1) {
- return 1;
- }
- return grid[m][n] = uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
- }
- }
當值不為0的時候說明已經被算過了,直接取就行了,否則就得計算并保存結果,這樣效率提高了不少,但是如果m和n特別大,遞歸層數過多時會造成堆棧溢出的,該怎么辦?這個時候就得用到動態規劃了
遞歸是從上至下開始計算的,有沒有可能從下而上的計算呢?,如先算出(1,2)和(2,1),然后就能算出(2,2)了,我們得按照一定的規律計算,保證在算(2,2)之前,(1,2)和(2,1)已經算完了,我們只要按行從左到右計算,或者按列從上到下即可
dp[i][j]表示到達第i行第j列的路徑數,所以狀態轉移方程為
- dp[i][j] = dp[i][j-1] + dp[i-1][j]
- class Solution {
- public static int[][] grid = new int[110][110];
- public int uniquePaths(int m, int n) {
- for (int i = 1; i <= n ; i++) {
- for (int j = 1; j <= m ; j++) {
- if (i == 1 || j == 1)
- grid[i][j] = 1;
- else
- grid[i][j] = grid[i][j-1] + grid[i-1][j];
- }
- }
- return grid[n][m];
- }
- }
減繩子
來源:《劍指offer》第二版
描述:給你一根長度為n的繩子,請把繩子剪成m段 (m和n都是整數,n>1并且m>1)每段繩子的長度記為k[0],k[1],…,k[m].請問k[0]k[1]…*k[m]可能的最大乘積是多少?例如,當繩子的長度為8時,我們把它剪成長度分別為2,3,3的三段,此時得到的最大乘積是18.
思路:定義函數f(n)為長度為n的繩子剪成若干段后各段長度乘積的最大值。在剪第一刀的時候,我們有n-1種可能的選擇,也就是剪出來的第一段繩子的長度分別為1,2...n-1。因此f(n)=max(f(i)*f(n-i)),其中0
假設dp[i]表示長度為i的繩子能得到的最大乘積,則狀態轉移方程為
- dp[i] = max(dp[i], dp[j] * dp[i-j])
- public class Solution {
- public int maxNumAfterCutting(int n) {
- if (n < 2)
- return 0;
- // 繩子長度為2時,只能剪成1和1
- if (n == 2)
- return 1;
- // 只可能為長度為1和2的2段或者長度都為1的三段,最大值為2
- if (n == 3)
- return 2;
- // 當長度大于3時,長度為3的段的最大值是3
- int product[] = new int[n+1];
- product[0] = 0;
- product[1] = 1;
- product[2] = 2;
- product[3] = 3;
- int max = 0;
- for (int i = 4; i <= n; i++) {
- max = 0;
- for (int j = 1; j <= i / 2; j++) {
- int sum = product[j] * product[i - j];
- if (sum > max) {
- max = sum;
- product[i] = max;
- }
- }
- }
- return product[n];
- }
- }
代碼中第一個for循環變量i是順序遞增的,這意味著計算順序是自下而上的。因此再求f(i)之前,對于每一個j(0值,這就是代碼中第二個for循環的功能<>
這個面試題又比第一個面試題難了一點,因為第一個面試題僅僅是將一個大問題劃分成幾個子問題,并沒有根據局部解進行決策得到最優解,而這個面試題體現了決策的過程
接雨水
來源:LeetCode 42. 接雨水
描述:給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖,計算按此排列的柱子,下雨之后能接多少雨水
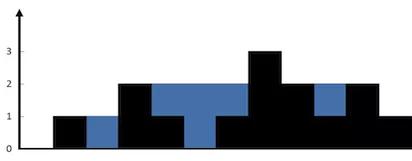
上面是由數組 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖,在這種情況下,可以接 6 個單位的雨水(藍色部分表示雨水)
示例:輸入: [0,1,0,2,1,0,1,3,2,1,2,1]輸出: 6
思路:思路還是比較簡單,對每一個柱子能存多少水求和即可,這樣只需要獲取這個柱子左邊的最高高度和這個柱子右邊的最高高度,2者的最小值減去柱子的高度就是這個柱子的存水量
- class Solution {
- public int trap(int[] height) {
- int sum = 0;
- for (int i = 0; i < height.length; i++) {
- int maxLeft = 0, maxRight = 0;
- // 對i這個柱子,左邊柱子的最高值
- for (int left = 0; left < i; left++) {
- maxLeft = Math.max(maxLeft, height[left]);
- }
- // 對i這個柱子,右邊柱子的最高值
- for (int right = i + 1; right < height.length ; right++) {
- maxRight = Math.max(maxRight, height[right]);
- }
- // i這個柱子能存的水量
- int temp = Math.min(maxLeft, maxRight) - height[i];
- if (temp > 0)
- sum += temp;
- }
- return sum;
- }
- }
每次都要算某個柱子的左右最值,時間復雜度是O(n2),能不能把算左右最值的效率提高呢?這就用到動態規劃了,假如說
我們用dp[i],表示到第i個柱子(包括第i個柱子)左邊的最大值,height[i]為第i個柱子的高度,右邊同理,則狀態轉移方程為
- dp[i] = max(dp[i-1], height[i])
- class Solution {
- public int trap(int[] height) {
- int sum = 0;
- int len = height.length;
- if (len == 0)
- return 0;
- int[] maxLeft = new int[len];
- int[] maxRight = new int[len];
- maxLeft[0] = height[0];
- for (int i = 1; i < len; i++) {
- maxLeft[i] = Math.max(height[i], maxLeft[i-1]);
- }
- maxRight[len - 1] = height[len - 1];
- for (int i = len - 2; i >= 0; i--) {
- maxRight[i] = Math.max(height[i] ,maxRight[i+1]);
- }
- for (int i = 0; i < height.length; i++) {
- sum += Math.min(maxLeft[i], maxRight[i]) - height[i];
- }
- return sum;
- }
- }
這樣時間復雜度就變成O(n)了
分割等和子集
來源:LeetCode 416. 分割等和子集
描述:給定一個只包含正整數的非空數組。是否可以將這個數組分割成兩個子集,使得兩個子集的元素和相等。
注意:
每個數組中的元素不會超過 100 數組的大小不會超過 200 示例 1:
- 輸入: [1, 5, 11, 5]
- 輸出: true
- 解釋: 數組可以分割成 [1, 5, 5] 和 [11].
示例 2:
- 輸入: [1, 2, 3, 5]
- 輸出: false
- 解釋: 數組不能分割成兩個元素和相等的子集.
思路:很典型的01背包,背包的容量為元素和的一半,最后看背包是否能填滿即可 之前已經說了01背包的狀態轉移方程
第i件物品的重量是w[i],價值是v[i] 用dp[i][j]表示前i件物品放入一個承重為j的背包可以獲得的最大價值,狀態轉移方程為
- dp[i][j] = max{dp[i-1][j], dp[i-1][j-w[i]] + c[i]}
即
- dp[i][j] = max{不放第i件物品,放第i件物品}
在這個題目中,承重和價值都是這個值的大小,因為上一次例子用到了壓縮數組的寫法,這次就換一種寫法,完全按照狀態轉移方程來
- public class Solution {
- public boolean canPartition(int[] nums) {
- int sum = 0;
- for (int i = 0; i < nums.length; i++) {
- sum += nums[i];
- }
- // 奇數直接false
- if ((sum & 1) == 1) {
- return false;
- }
- int target = sum >> 1;
- int[][] dp = new int[nums.length][target + 1];
- for (int i = 0; i < nums.length; i++) {
- for (int j = 0; j <= target; j++) {
- if (j >= nums[i]) {
- if (i == 0) {
- dp[i][j] = nums[i];
- } else {
- dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
- }
- }
- }
- }
- return dp[nums.length - 1][target] == target;
- }
- }
本文轉載自微信公眾號「Java識堂」,可以通過以下二維碼關注。轉載本文請聯系Java識堂公眾號。