本文轉(zhuǎn)載自微信公眾號「zartbot」，作者扎波特的網(wǎng)線鉗。轉(zhuǎn)載本文請聯(lián)系zartbot公眾號。

昨天在公司看到一張PPT,上面寫著兩行大字:

SR for Anything, Network as a Computer

不用打聽寫這個ppt的人是誰，也不評價對錯惹是非，下面只想給網(wǎng)絡(luò)工程師技術(shù)扶貧一下可計算性和圖靈完備的知識，留給各位自己判斷.

圖靈機

圖靈機是英國數(shù)學(xué)家阿蘭·圖靈在1936年的文章《On Computable Numbers, with an Application to the Entscheidungsproblem》中提出的抽象計算模型.

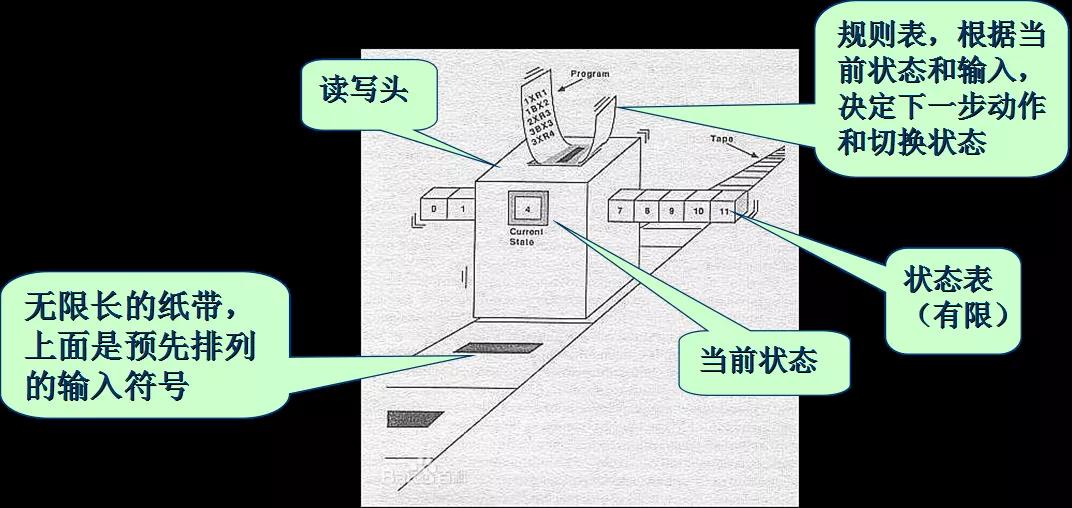
在論文的第三章講述了一個計算機的例子，即一個機器包含了一條無限長的紙帶，紙帶被分成一些Square，然后上面有一些二進制編碼的symbol。存在一個事先約定好的指令， 例如R表示機器將掃描右側(cè)的Square，同理L表示左側(cè)，E表示擦除,P表示打印等.計算即根據(jù)讀寫頭和規(guī)則表決定動作，當(dāng)讀寫頭停機時，打印輸出的就是計算結(jié)果：

圖靈完備

圖靈完備是指，當(dāng)你設(shè)計了一套操作數(shù)據(jù)的規(guī)則后，這套指令集或者語言能夠模擬圖靈機，那么就說這套規(guī)則是圖靈完備的。通常很多編程語言的圖靈完備性影響主要需要考慮分支Branch和循環(huán)loop的問題。當(dāng)然有一些語言故意設(shè)計成非圖靈完備的，例如很多區(qū)塊鏈的合約執(zhí)行指令不支持分支跳轉(zhuǎn)和循環(huán)，主要的目的是它使用的場景和安全性考慮決定的。

SR的圖靈完備

SR本身的編碼上來看，并不是圖靈完備的. 因為SR Label只能順序執(zhí)行。當(dāng)然也可以做一些特殊的處理，例如Binding-SID可以看做是一個特殊的函數(shù)調(diào)用，然后借用MPLS Stack的結(jié)構(gòu)，可以實現(xiàn)函數(shù)入棧. 同時我們也可以定義一些特殊的Label行為來進行Label跳轉(zhuǎn), 但又有另一個缺陷，處理報文的時候，我們并沒有設(shè)計相應(yīng)的狀態(tài)機。如果要設(shè)計，又會成為一個Stateful的forwarding feature，需要相應(yīng)的流表和動態(tài)狀態(tài)更新。

某種意義上來講，MPLS-SR因為有棧的結(jié)構(gòu)，入棧和彈出標(biāo)簽相對容易。而SRv6則是一個工程上的災(zāi)難，由于必須保留報文的源IP地址，一方面有uRPF的缺陷，另一方面維持IP頭并要同時操作SRH產(chǎn)生了一系列問題，例如交換機通常沒法同時處理這么大量的數(shù)據(jù)，SRv6標(biāo)簽棧深度受限。

而針對棧結(jié)構(gòu)，SRv6的SRH在報文中間。入棧和出棧對于P4一類的交換機容易，Deparser上插進去或者砍掉就好。但是傳統(tǒng)的CPU架構(gòu)而言，都需要大量的memory move的操作，我還在開玩笑，Intel啥時候能夠出一個批量操作I/O的deparser呢，集成在網(wǎng)卡上或者CPU上都行....

在設(shè)計的時候，如果能丟棄原有的IPv6頭，根據(jù)SRH的信息重建便是一個更好的解決方案，這樣標(biāo)簽入棧出棧的處理相對容易很多，uRPF的缺陷也可以避免。所以反過來你就能明白RFC8663 MPLS-SR over UDP的能夠在很多場景被接受的原因。但是很抱歉MPLS-SR的問題來自于標(biāo)簽棧的長度，以及沒有類似于SRv6那樣定義的

P4的圖靈完備

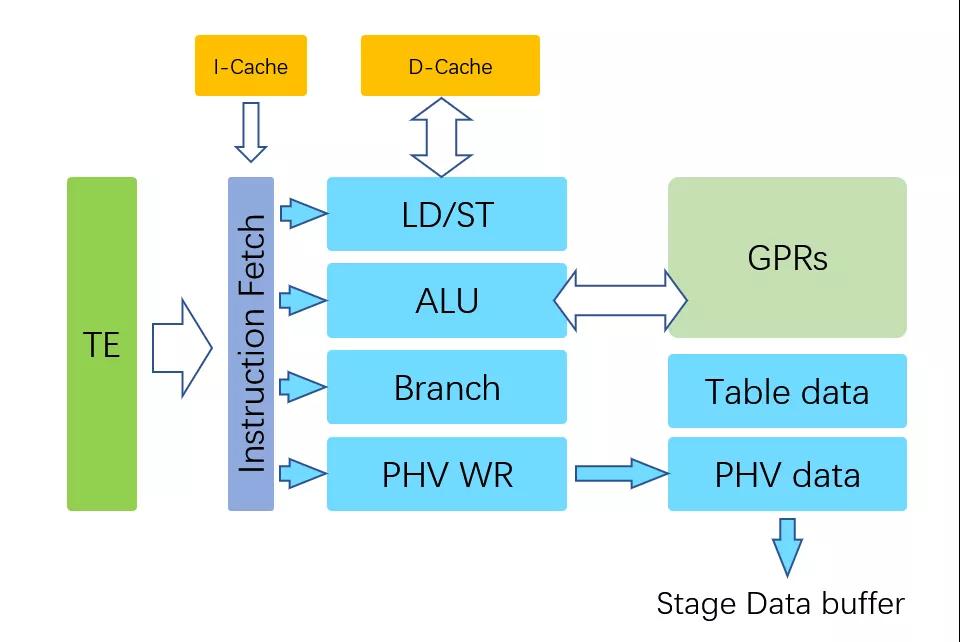
我們來看另一個問題，P4設(shè)計之初是完全基于硬件能力的，一旦涉及分支Branch極易帶來流水線的Stall，因此P4早期的MAU并沒有打算支持分支預(yù)測，更多的是采用match不同的表產(chǎn)生新的action來將流量分擔(dān)到另一個MAU實現(xiàn)的。Torfino-2增加了一些功能，而為了實現(xiàn)更加靈活多樣的計算，Pensando的實現(xiàn)中直接增加了寄存器/PC/Branch器件.

而NanoPU更是直接把一個處理器堆到了P4 MAU旁邊。

網(wǎng)絡(luò)是否需要圖靈完備編程

很多人總是喜歡一招鮮打遍天下，但真的有必要什么都做么?前段時間有個某云的同學(xué)發(fā)了一個朋友圈說什么指標(biāo)都要追求世界第一， 我補了一句那么價格肯定也世界第一。成年人有足夠的支持時可以輕松的說不需要選擇，都要。但是技術(shù)總是需要取舍的。加法容易減法難，就是這個道理。

計算、存儲、網(wǎng)絡(luò)這三者的組合有其內(nèi)在的精妙，存內(nèi)計算(In Memory Computing)和邊緣計算提出的算力網(wǎng)絡(luò)都是為了解決馮諾依曼架構(gòu)的缺陷，使得計算規(guī)模能夠再上一個臺階。但是另一個可信計算的問題又會困擾大家。

架構(gòu)上我并不認同網(wǎng)絡(luò)能夠?qū)崿F(xiàn)大量的圖靈完備的計算，而是可以通過一系列組合為計算和存儲搭起一個更好的橋梁。