MySQL 一棵 B+ 樹能存多少條數據?
本文轉載自微信公眾號「微觀技術」,作者TomGE 。轉載本文請聯系微觀技術公眾號。
大家好,我是Tom哥~
今日寄語:充滿活力的新人,能讓身邊的人都重回初心,真是不可思議。
mysql 的InnoDB存儲引擎 一棵B+樹可以存放多少行數據?
(答案在文章中!!)
要搞清楚這個問題,首先要從InnoDB索引數據結構、數據組織方式說起。
我們都知道計算機有五大組成部分:控制器,運算器,存儲器,輸入設備,輸出設備。
其中很重要的,也跟今天這個題目有關系的是存儲器。
我們知道萬事萬物都有自己的單元體系,若干個小單體組成一個個大的個體。就像拼樂高一樣,可以自由組合。所以說,如果能熟悉最小單元,就意味著我們抓住了事物的本事,再復雜的問題也會迎刃而解。
存儲單元
存儲器范圍比較大,但是數據具體怎么存儲,有自己的最小存儲單元。
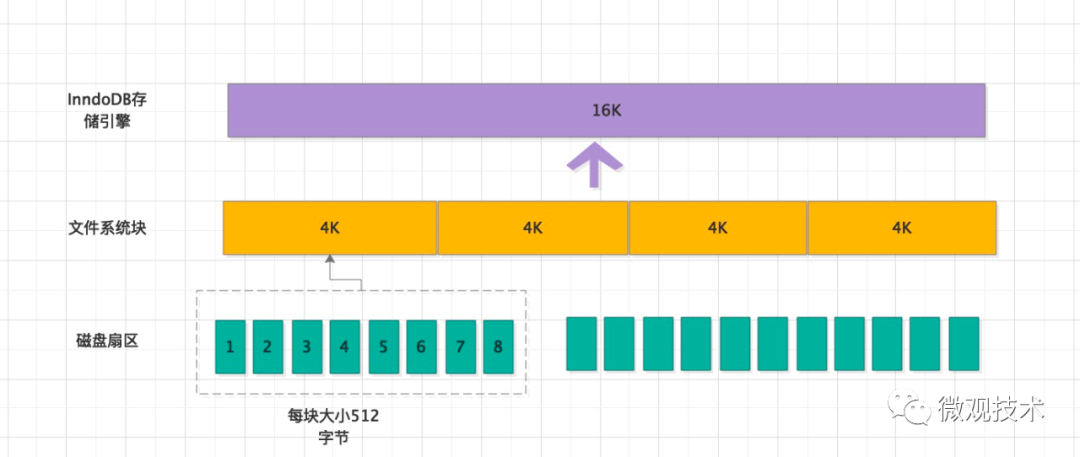
1、數據持久化存儲磁盤里,磁盤的最小單元是扇區,一個扇區的大小是 512個字節
2、文件系統的最小單元是塊,一個塊的大小是 4K
3、InnoDB存儲引擎,有自己的最小單元,稱之為頁,一個頁的大小是16K
扇區、塊、頁這三者的存儲關系?
InnoDB引擎
如果mysql部署在本地,通過命令行方式連接mysql,默認的端口 3306 ,然后輸入密碼即可進入
- mysql -u root -p
查看InnoDB的頁大小
- show variables like 'innodb_page_size';
mysql數據庫中,table表中的記錄都是存儲在頁中,那么一頁可以存多少行數據?假如一行數據的大小約為1K字節,那么按 16K / 1K = 16,可以計算出一頁大約能存放16條數據。
mysql 的最小存儲單元叫做“頁”,這么多的頁是如何構建一個龐大的數據組織,我們又如何知道數據存儲在哪一個頁中?
如果逐條遍歷,性能肯定很差。為了提升查找速度,我們引入了B+樹,先來看下B+樹的存儲結構
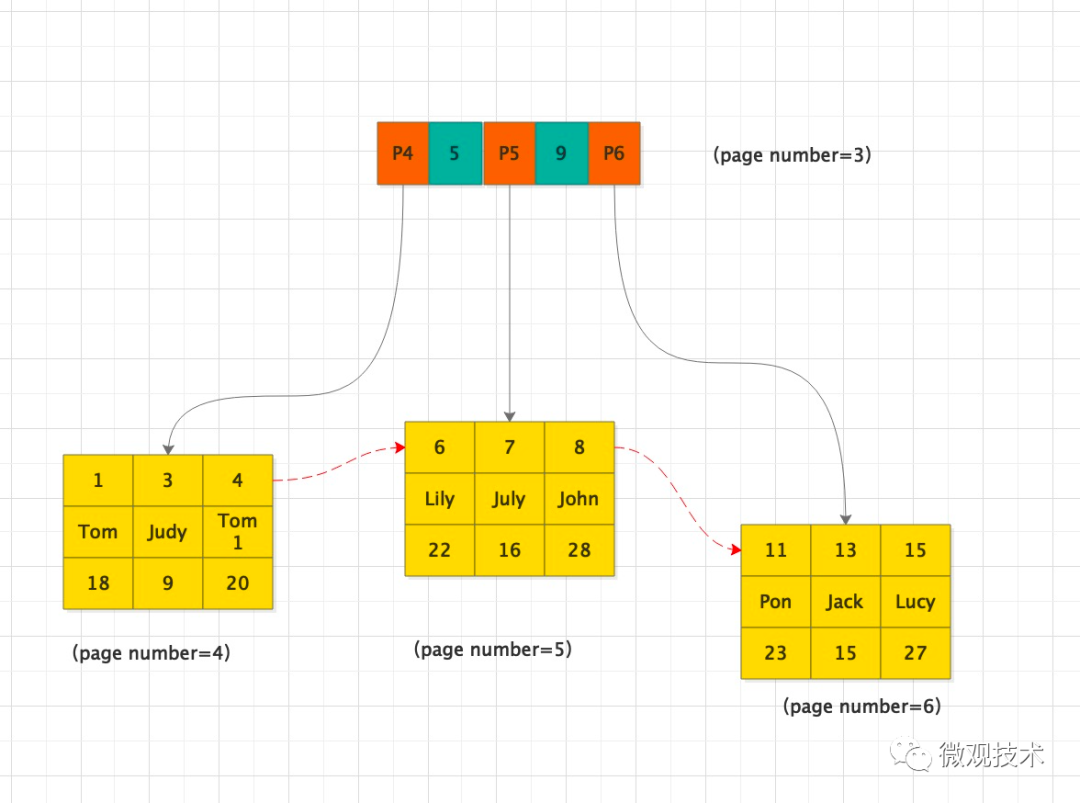
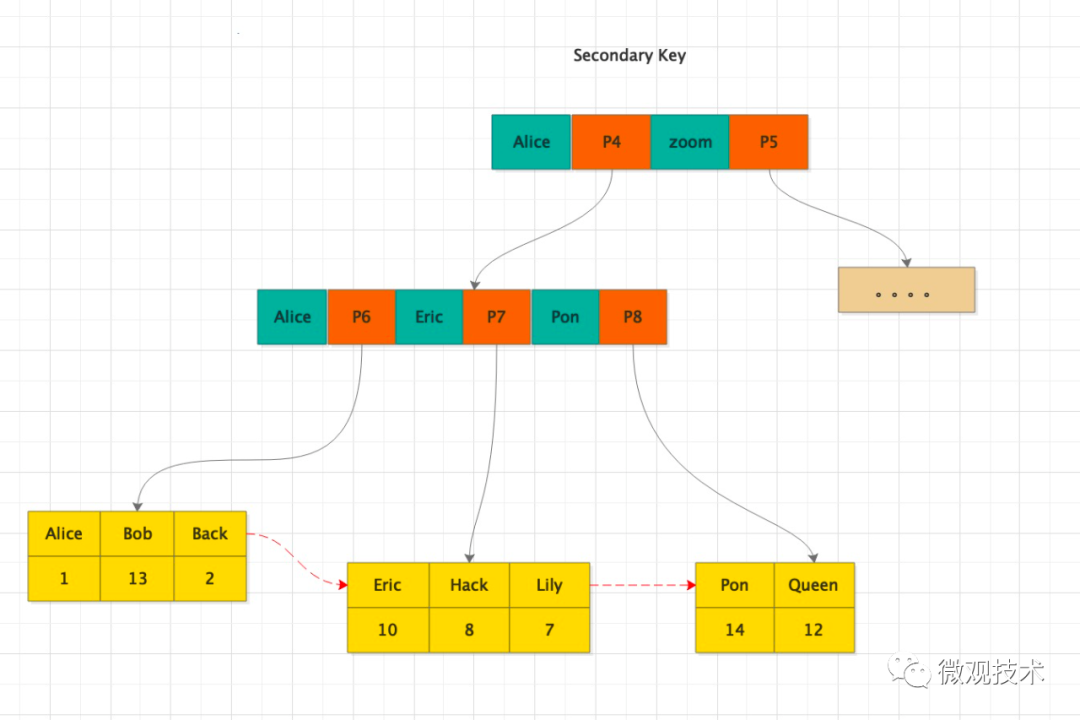
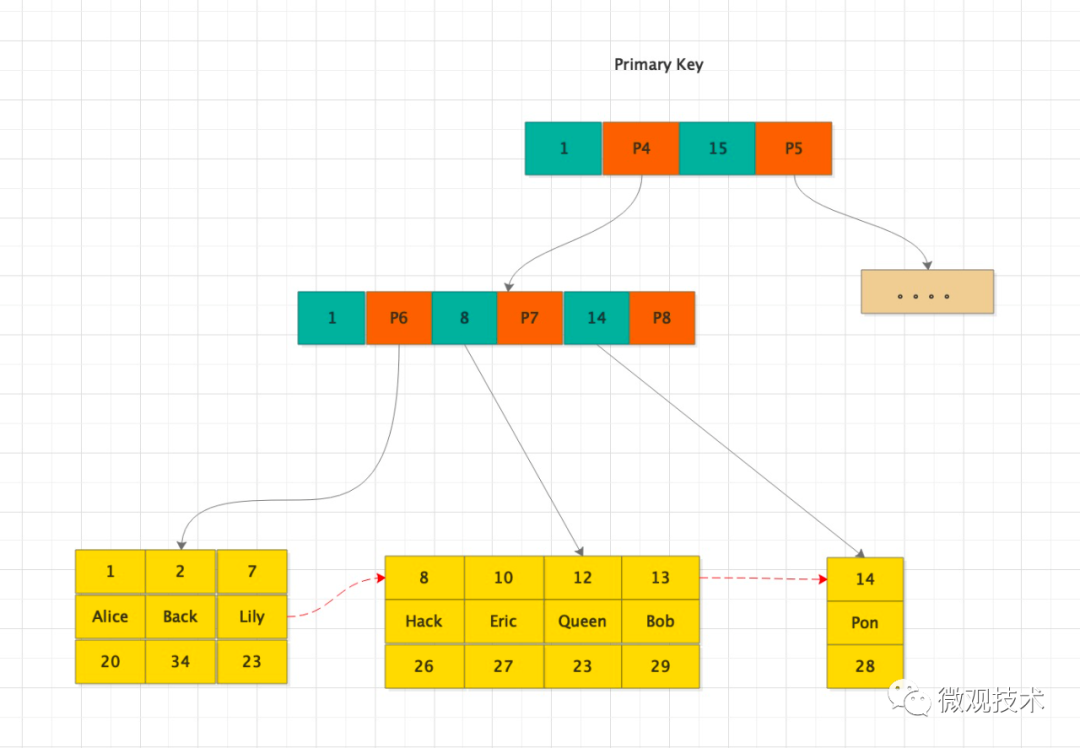
頁除了可以存放數據(葉子節點),還可以存放健值和指針(非葉子節點),當然他們是有序的。這樣的數據組織形式,我們稱為索引組織表。
如:上圖中 page number=3的頁,該頁存放鍵值和指向數據頁的指針,這樣的頁由N個鍵值+指針組成
B+ 樹是如何檢索記錄?
- 首先找到根頁,你怎么知道一張表的根頁在哪呢?
- 其實每張表的根頁位置在表空間文件中是固定的,即page number=3的頁
- 找到根頁后通過二分查找法,定位到id=5的數據應該在指針P5指向的頁中
- 然后再去page number=5的頁中查找,同樣通過二分查詢法即可找到id=5的記錄
如何計算B+樹的高度?
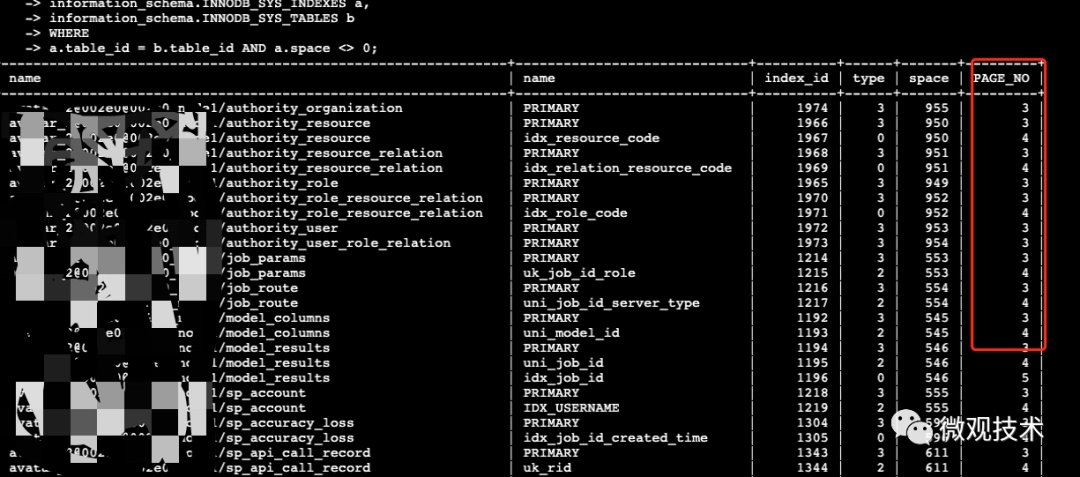
在InnoDB 的表空間文件中,約定page number = 3表示主鍵索引的根頁
- SELECT
- b.name, a.name, index_id, type, a.space, a.PAGE_NO
- FROM
- information_schema.INNODB_SYS_INDEXES a,
- information_schema.INNODB_SYS_TABLES b
- WHERE
- a.table_id = b.table_id AND a.space <> 0
- and b.name like '%sp_job_log';
從圖中可以看出,每個表的主鍵索引的根頁的page number都是3,而其他的二級索引page number為4
在根頁偏移量為64的地方存放了該B+樹的page level。主鍵索引B+樹的根頁在整個表空間文件中的第3個頁開始,所以算出它在文件中的偏移量:16384*3 + 64 = 49152 + 64 =49216,前2個字節中。
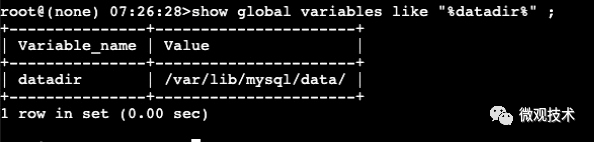
首先,找到MySql數據庫物理文件存放位置:
- show global variables like "%datadir%" ;
hexdump工具,查看表空間文件指定偏移量上的數據:
- hexdump -s 49216 -n 10 sp_job_log.ibd
page_level 值是 1,那么 B+樹高度為 page level + 1 = 2
特別說明:
- 查詢數據庫時,不論讀一行,還是讀多行,都是將這些行所在的整頁數據加載,然后在內存中匹配過濾出最終結果。
- 表的檢索速度跟樹的深度有直接關系,畢竟一次頁加載就是一次IO,而磁盤IO又是比較費時間。對于一張千萬級條數B+樹高度為3的表與幾十萬級B+樹高度也為3的表,其實查詢效率相差不大。
一棵樹可以存放多少行數據?
假設B+樹的深度為2
這棵B+樹的存儲總記錄數 = 根節點指針數 * 單個葉子節點記錄條數
那么指針數如何計算?
假設主鍵ID為bigint類型,長度為8字節,而指針大小在InnoDB源碼中設置為6字節,這樣一共14字節。
那么一個頁中能存放多少這樣的組合,就代表有多少指針,即 16384 / 14 = 1170。那么可以算出一棵高度為2 的B+樹,能存放 1170 * 16 = 18720 條這樣的數據記錄。
同理:
高度為3的B+樹可以存放的行數 = 1170 * 1170 * 16 = 21902400
千萬級的數據存儲只需要約3層B+樹,查詢數據時,每加載一頁(page)代表一次IO。所以說,根據主鍵id索引查詢約3次IO便可以找到目標結果。
對于一些復雜的查詢,可能需要走二級索引,那么通過二級索引查找記錄最多需要花費多少次IO呢?
首先,從二級索引B+樹中,根據name 找到對應的主鍵id
然后,再根據主鍵id 從 聚簇索引查找到對應的記錄。如上圖所示,二級索引有3層,聚簇索引有3層,那么最多花費的IO次數是:3+3 = 6
聚簇索引默認是主鍵,如果表中沒有定義主鍵,InnoDB 會選擇一個唯一的非空索引代替。如果沒有這樣的索引,InnoDB 會隱式定義一個主鍵來作為聚簇索引。
這也是為什么InnoDB表必須有主鍵,并且推薦使用整型的自增主鍵!!!
InnoDB使用的是聚簇索引,將主鍵組織到一棵B+樹中,而行數據就儲存在葉子節點上
舉例說明:
1、若使用"where id = 14"這樣的條件查找記錄,則按照B+樹的檢索算法即可查找到對應的葉節點,之后獲得行數據。
2、若對Name列進行條件搜索,則需要兩個步驟:
第一步在輔助索引B+樹中檢索Name,到達其葉子節點獲取對應的主鍵值。
第二步使用主鍵值在主索引B+樹中再執行一次B+樹檢索操作,最終到達葉子節點即可獲取整行數據。(重點在于通過其他鍵需要建立輔助索引)
實戰演示
實際項目中,每個表的結構設計都不一樣,占用的存儲空間大小也各不相等。如何計算不同的B+樹深度下,一個表可以存儲的記錄條數?
我們以業務日志表 sp_job_log 為例,講解詳細的計算過程:
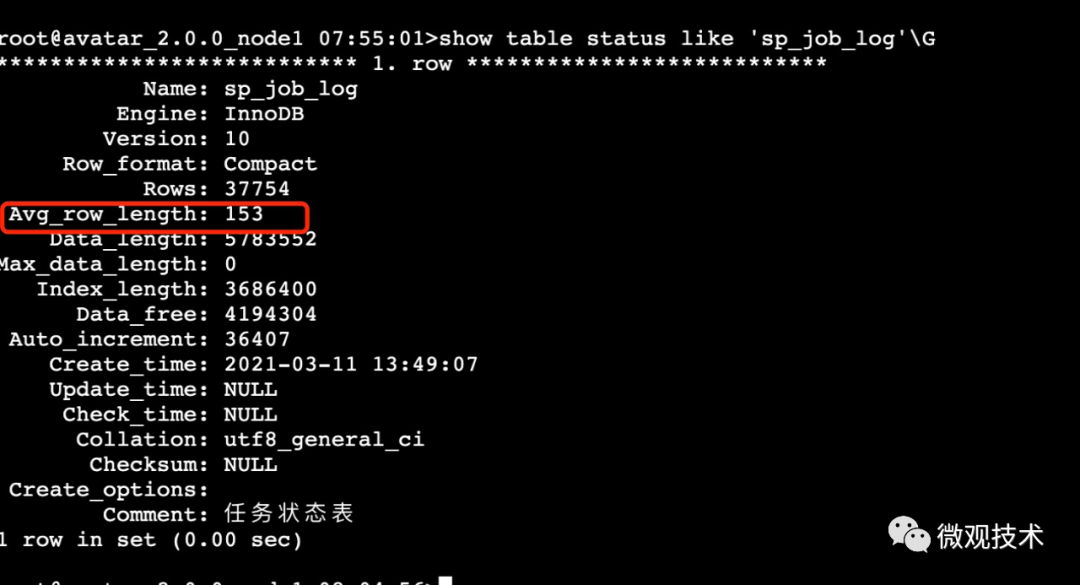
1、查看表的狀態信息
- show table status like 'sp_job_log'\G
圖中看到sp_job_log表的行平均大小為153個字節
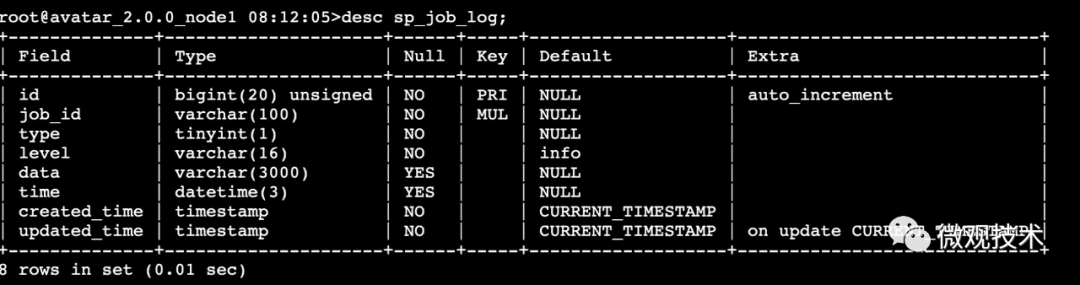
2、查看表結構
- desc sp_job_log;
3、計算B+樹的行數
單個葉子節點(頁)中的記錄數 = 16K / 153 = 105
非葉子節點能存放多少指針, 16384 / 14 = 1170
如果樹的高度為3,可以存放的記錄行數 = 1170 * 1170 * 105 = 143,734,500
最后加餐
普通索引和唯一索引在查詢效率上有什么不同?
唯一索引就是在普通索引上增加了約束性,也就是關鍵字唯一,找到了關鍵字就停止檢索。而普通索引,可能會存在用戶記錄中的關鍵字相同的情況,根據頁結構的原理,當我們讀取一條記錄的時候,不是單獨將這條記錄從磁盤中讀出去,而是將這個記錄所在的頁全部加載到內存中進行讀取。InnoDB 存儲引擎的頁大小為 16KB,在一個頁中可能存儲著上千個記錄,因此在普通索引的字段上進行查找也就是在內存中多幾次判斷下一條記錄的操作,對于 CPU 來說,這些操作所消耗的時間是可以忽略不計的。所以對一個索引字段進行檢索,采用普通索引還是唯一索引在檢索效率上基本上沒有差別。