如何更快地將String轉換成Int/Long

作者：kiritomoe 2021-08-31 09:12:18

在很多追求性能的程序挑戰賽中，經常會遇到一個操作：將 String 轉換成 Integer/Long。如果你沒有開發過高并發的系統，或者沒有參加過任何性能挑戰賽，可能會有這樣的疑問：這有啥好講究的，Integer.valueOf/Long.valueOf 又不是不能用。

[[420585]]

你好鴨，Kirito 今天又來分享性能優化的騷操作了。

在很多追求性能的程序挑戰賽中，經常會遇到一個操作：將 String 轉換成 Integer/Long。如果你沒有開發過高并發的系統，或者沒有參加過任何性能挑戰賽，可能會有這樣的疑問：這有啥好講究的，Integer.valueOf/Long.valueOf 又不是不能用。實際上，很多內置的轉換工具類只滿足了功能性的需求，在高并發場景下，可能會是熱點方法，成為系統性能的瓶頸。

文章開頭，我先做一下說明，本文的測試結論出自：https://kholdstare.github.io/technical/2020/05/26/faster-integer-parsing.html 。測試代碼基于 C++，我會在翻譯原文的同時，添加了部分自己的理解，以協助讀者更好地理解其中的細節。

問題提出

假設現在有一些文本信息，固定長度為 16 位，例如下文給出的時間戳，需要盡可能快地解析這些時間戳

timestamp 
1585201087123567 
1585201087123585 
1585201087123621

方法體如下所示：

std::uint64_t parse_timestamp(std::string_view s) 
{ 
  // ??? 
}

問題提出后，大家不妨先思考下，如果是你，你會采取什么方案呢?帶著這樣的思考，我們進入下面的一個個方案。

Native 方案

我們有哪些現成的轉換方案呢?

繼承自 C 的 std::atoll
std::stringstream
C++17 提供的 charconv
boost::spirit::qi

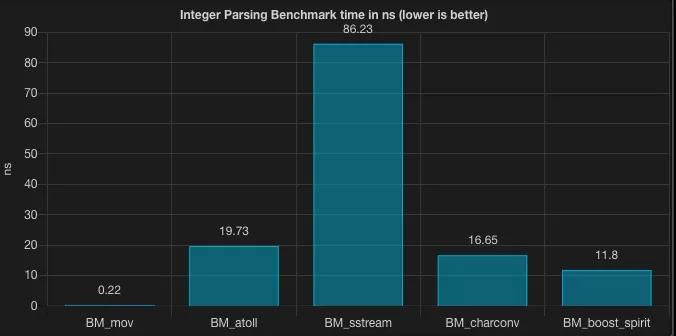
評測程序采用 Google Benchmark 進行對比評測。同時，我們以不做任何轉換的方案來充當 baseline，以供對比。(baseline 方案在底層，相當于將數值放進來了寄存器中，所以命名成了 BM_mov)

下面給出的評測代碼不是那么地關鍵，只是為了給大家展示評測是如何運行的。

static void BM_mov(benchmark::State& state) { 
  for (auto _ : state) { 
    benchmark::DoNotOptimize(1585201087123789); 
  } 
} 
 
static void BM_atoll(benchmark::State& state) { 
  for (auto _ : state) { 
    benchmark::DoNotOptimize(std::atoll(example_timestamp)); 
  } 
} 
 
static void BM_sstream(benchmark::State& state) { 
  std::stringstream s(example_timestamp); 
  for (auto _ : state) { 
    s.seekg(0); 
    std::uint64_t i = 0; 
    s >> i; 
    benchmark::DoNotOptimize(i); 
  } 
} 
static void BM_charconv(benchmark::State& state) { 
  auto s = example_timestamp; 
  for (auto _ : state) { 
    std::uint64_t result = 0; 
    std::from_chars(s.data(), s.data() + s.size(), result); 
    benchmark::DoNotOptimize(result); 
  } 
} 
 
static void BM_boost_spirit(benchmark::State& state) { 
  using boost::spirit::qi::parse; 
  for (auto _ : state) { 
    std::uint64_t result = 0; 
    parse(s.data(), s.data() + s.size(), result); 
    benchmark::DoNotOptimize(result); 
  } 
}

Native

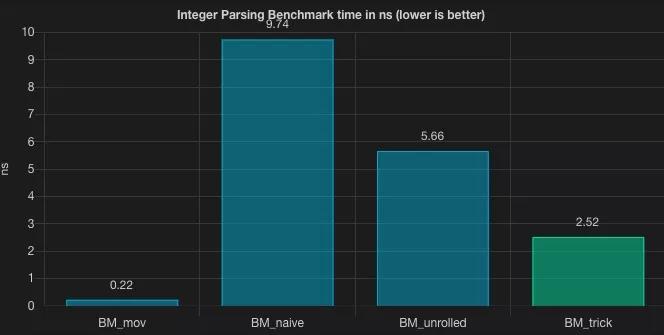
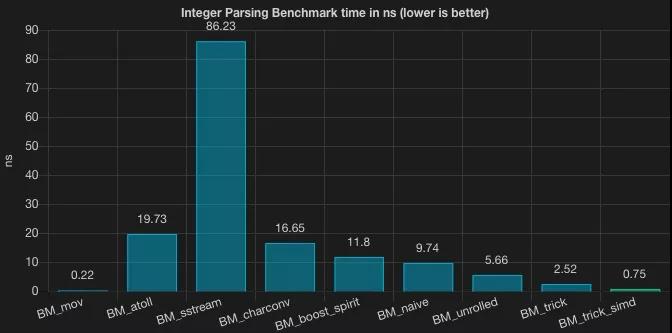
可以發現 stringstream 表現的非常差。當然，這并不是一個公平的比較，但從測評結果來看，使用 stringstream 來實現數值轉換相比 baseline 慢了 391 倍。相比之下，和 boost::spirit 表現的更好。

既然我們已經知道了目標字符串包含了要解析的數字，而且不需要做任何的數值校驗，基于這些前提，我們可以思考下，還有更快的方案嗎?

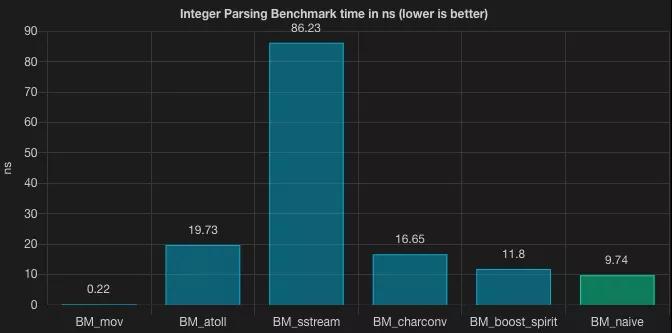
Naive 方案

我們可以通過一個再簡單不過的循環方案，一個個地解析字符。

inline std::uint64_t parse_naive(std::string_view s) noexcept 
{ 
  std::uint64_t result = 0; 
  for(char digit : s) 
  { 
    result *= 10; 
    result += digit - '0'; 
  } 
  return result; 
}

Naive

雖然這層 for 循環看起來呆呆的，但如果這樣一個呆呆的解決方案能夠擊敗標準庫實現，何樂而不為呢?前提是，標準庫的實現考慮了異常場景，做了一些校驗，這種 for 循環寫法的一個前提是，我們的輸入一定是合理的。

之前我的文章也提到過這個方案。顯然， naive 的方案之后還會有更優的替代方案。

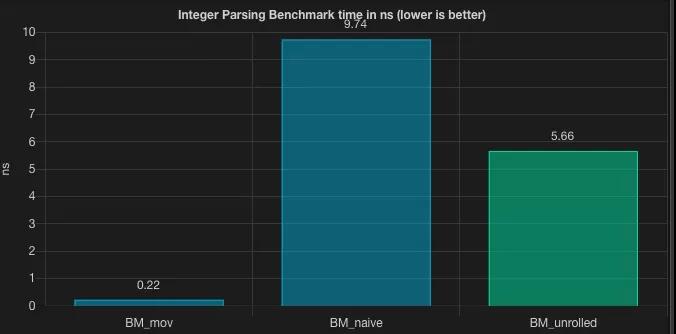
循環展開方案

記得我們在文章的開頭加了一個限定，限定了字符串長度固定是 16 位，所以循環是可以被省略的，循環展開之后，方案可以更快。

inline std::uint64_t parse_unrolled(std::string_view s) noexcept 
{ 
  std::uint64_t result = 0; 
 
  result += (s[0] - '0') * 1000000000000000ULL; 
  result += (s[1] - '0') * 100000000000000ULL; 
  result += (s[2] - '0') * 10000000000000ULL; 
  result += (s[3] - '0') * 1000000000000ULL; 
  result += (s[4] - '0') * 100000000000ULL; 
  result += (s[5] - '0') * 10000000000ULL; 
  result += (s[6] - '0') * 1000000000ULL; 
  result += (s[7] - '0') * 100000000ULL; 
  result += (s[8] - '0') * 10000000ULL; 
  result += (s[9] - '0') * 1000000ULL; 
  result += (s[10] - '0') * 100000ULL; 
  result += (s[11] - '0') * 10000ULL; 
  result += (s[12] - '0') * 1000ULL; 
  result += (s[13] - '0') * 100ULL; 
  result += (s[14] - '0') * 10ULL; 
  result += (s[15] - '0'); 
 
  return result; 
}

unrolled

關于循環展開為什么會更快，可以參考我過去關于 JMH 的文章。

byteswap 方案

先思考下，如果繼續圍繞上述的方案進行，我們可能只有兩個方向：

并發執行加法和乘法計算，但這種 CPU 操作似乎又不能通過多線程之類的手段進行加速，該如何優化是個問題

將乘法和加法運算轉換成位運算，獲得更快的 CPU 執行速度，但如果轉換又是個問題

相信讀者們都會有這樣的疑問，那我們繼續帶著這樣疑問往下看原作者的優化思路是什么。

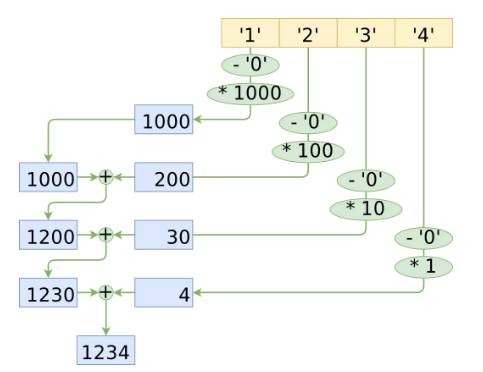
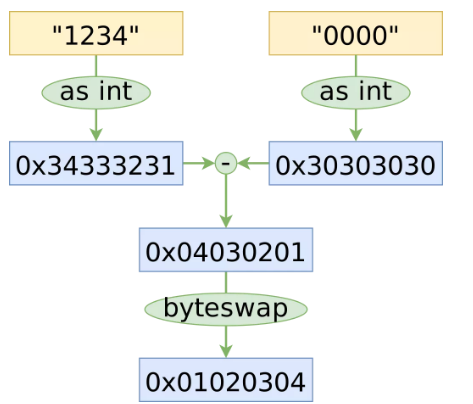
緊接著上述的循環展開方案，將 “1234” 解析為 32 位整數對應的循環展開操作繪制為圖，過程如下：

Unrolled solution graph

我們可以看到，乘法和加法的操作次數跟字符的數量是線性相關的。由于每一次乘法都是由不同的乘數進行，所以我們不能只乘“一次”，在乘法的最后，我們還需要將所有結果相加。乍一看，好像很難優化。

下面的優化技巧，需要一些操作系統、編譯原理相關的知識作為輔助，你需要了解 byteswap 這個系統調用，了解大端序和小端序的字節序表示方法(后面我也會分享相關的文章)，如果你不關心這些細節，也可以直接跳到本段的最后，直接看結論。

理解清楚下圖的含義，需要理解幾個概念：

字符 1 對應的 ascii 值是 31，相應的 2 對應 32，4 對應 34
在小端序機器上(例如 x86)，字符串是以大端序存儲的，而 Integer 是以小端序存儲的
byteswap 可以實現字節序調換

byteswap

上圖展示了十六進制表示下的轉換過程，可以在更少的操作下達到最終的解析狀態。

將上圖的流程使用 C++ 來實現，將 String 重新解釋為 Integer，必須使用 std::memcpy(避免命名沖突)，執行相減操作，然后通過編譯器內置的 __builtin_bswap64 在一條指令中交換字節。到目前為止，這是最快的一個優化。

template <typename T> 
inline T get_zeros_string() noexcept; 
 
template <> 
inline std::uint64_t get_zeros_string<std::uint64_t>() noexcept 
{ 
  std::uint64_t result = 0; 
  constexpr char zeros[] = "00000000"; 
  std::memcpy(&result, zeros, sizeof(result)); 
  return result; 
} 
 
inline std::uint64_t parse_8_chars(const char* string) noexcept 
{ 
  std::uint64_t chunk = 0; 
  std::memcpy(&chunk, string, sizeof(chunk)); 
  chunk = __builtin_bswap64(chunk - get_zeros_string<std::uint64_t>()); 
 
  // ... 
}

我們看上去得到了想要的結果，但是這個方案從時間復雜度來看，仍然是 O(n) 的，是否可以在這個方案的基礎上，繼續進行優化呢?

分治方案

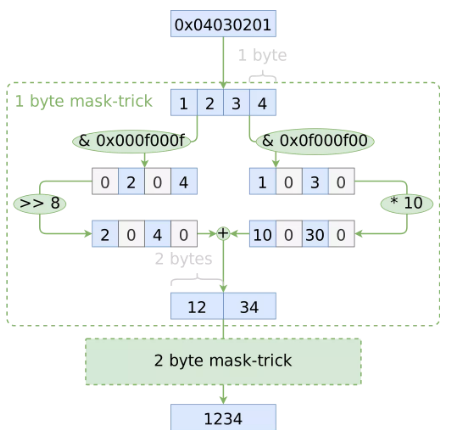
從最初的 Native 方案，到上一節的 byteswap 方案，我們都只是優化了 CPU 操作，并沒有優化復雜度，既然不滿足于 O(n)，那下一個復雜度可能性是什么?O(logn)!我們可以將每個相鄰的數字組合成一對，然后將每對數字繼續組合成一組四個，依此類推，直到我們得到整個整數。

如何同時處理鄰近的數字，這是讓算法跑進 O(logn) 的關鍵

該方案的關鍵之處在于：將偶數位的數字乘以 10 的冪，并且單獨留下奇數位的數字。這可以通過位掩碼(bitmasking)來實現

分治方案

通過 bitmasking，我們可以一次對多個數字進行操作，將它們組合成一個更大的組合

通過使用這個掩碼技巧來實現前文提到的 parse_8_chars 函數。使用 bitmasking 的另一好處在于，我們不用減去 '0' ，因為位掩碼的副作用，使得我們正好可以省略這一步。

inline std::uint64_t parse_8_chars(const char* string) noexcept 
{ 
  std::uint64_t chunk = 0; 
  std::memcpy(&chunk, string, sizeof(chunk)); 
 
  // 1-byte mask trick (works on 4 pairs of single digits) 
  std::uint64_t lower_digits = (chunk & 0x0f000f000f000f00) >> 8; 
  std::uint64_t upper_digits = (chunk & 0x000f000f000f000f) * 10; 
  chunk = lower_digits + upper_digits; 
 
  // 2-byte mask trick (works on 2 pairs of two digits) 
  lower_digits = (chunk & 0x00ff000000ff0000) >> 16; 
  upper_digits = (chunk & 0x000000ff000000ff) * 100; 
  chunk = lower_digits + upper_digits; 
 
  // 4-byte mask trick (works on pair of four digits) 
  lower_digits = (chunk & 0x0000ffff00000000) >> 32; 
  upper_digits = (chunk & 0x000000000000ffff) * 10000; 
  chunk = lower_digits + upper_digits; 
 
  return chunk; 
}

trick 方案

綜合前面兩節，解析 16 位的數字，我們將它分成兩個 8 字節的塊，運行剛剛編寫的 parse_8_chars，并對其進行基準測試!

inline std::uint64_t parse_trick(std::string_view s) noexcept 
{ 
  std::uint64_t upper_digits = parse_8_chars(s.data()); 
  std::uint64_t lower_digits = parse_8_chars(s.data() + 8); 
  return upper_digits * 100000000 + lower_digits; 
} 
 
static void BM_trick(benchmark::State& state) { 
  for (auto _ : state) { 
    benchmark::DoNotOptimize(parse_trick(example_stringview)); 
  } 
}

trick

看上去優化的不錯，我們將循環展開方案的基準測試優化了近 56% 的性能。能做到這一點，主要得益于我們手動進行一系列 CPU 優化的操作，雖然這些并不是特別通用的技巧。這樣算不算開了個不好的頭呢?我們看起來對 CPU 操作干預地太多了，或許我們應該放棄這些優化，讓 CPU 自由地飛翔。

SIMD trick 方案

你是不是以為上面已經是最終方案了呢?不，優化還剩最后一步。

我們已經得到了一個結論

同時組合多組數字以實現 O(logn) 復雜度

如果有 16 個字符或 128 位的字符串要解析，還可以使用 SIMD。感興趣的讀者可以參考SIMD stands for Single Instruction Multiple Data。Intel 和 AMD CPU 都支持 SSE 和 AVX 指令，并且它們通常使用更寬的寄存器。

SIMA 簡單來說就是一組 CPU 的擴展指令，可以通過調用多組寄存器實現并行的乘法運算，從而提升系統性能。我們一般提到的向量化運算就是 SIMA。

讓我們先設置 16 個字節中的每一個數字：

inline std::uint64_t parse_16_chars(const char* string) noexcept 
{ 
  auto chunk = _mm_lddqu_si128( 
    reinterpret_cast<const __m128i*>(string) 
  ); 
  auto zeros =  _mm_set1_epi8('0'); 
  chunk = chunk - zeros; 
   
  // ... 
}

現在，主角變成了 madd 該系統調用。這些 SIMD 函數與我們使用位掩碼技巧所做的操作完全一樣——它們采用同一個寬寄存器，將其解釋為一個由較小整數組成的向量，每個乘以一個特定的乘數，然后將相鄰位的結果相加到一個更寬的整數向量中。所有操作一步完成。

// The 1-byte "trick" in one instruction 
const auto mult = _mm_set_epi8( 
  1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10 
); 
chunk = _mm_maddubs_epi16(chunk, mult);

2 字節方案其實還有另一條指令，但不幸的是我并沒有找到 4 字節方案的指令，還是需要兩條指令。這是完整的 parse_16_chars 方案：

inline std::uint64_t parse_16_chars(const char* string) noexcept 
{ 
  auto chunk = _mm_lddqu_si128( 
    reinterpret_cast<const __m128i*>(string) 
  ); 
  auto zeros =  _mm_set1_epi8('0'); 
  chunk = chunk - zeros; 
 
  { 
    const auto mult = _mm_set_epi8( 
      1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10 
    ); 
    chunk = _mm_maddubs_epi16(chunk, mult); 
  } 
  { 
    const auto mult = _mm_set_epi16(1, 100, 1, 100, 1, 100, 1, 100); 
    chunk = _mm_madd_epi16(chunk, mult); 
  } 
  { 
    chunk = _mm_packus_epi32(chunk, chunk); 
    const auto mult = _mm_set_epi16(0, 0, 0, 0, 1, 10000, 1, 10000); 
    chunk = _mm_madd_epi16(chunk, mult); 
  } 
 
  return ((chunk[0] & 0xffffffff) * 100000000) + (chunk[0] >> 32); 
}

SIMD trick

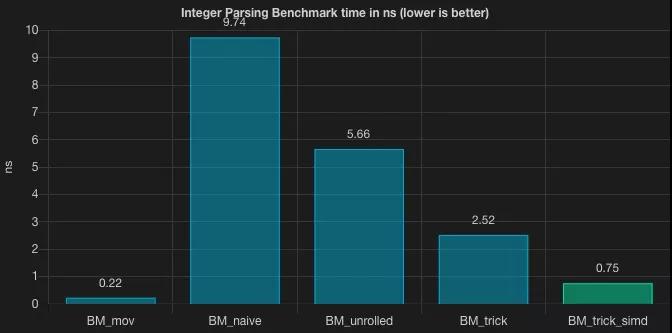
0.75 nanoseconds! 是不是大吃一驚呢.

總結

整體對比

有人可能會問，你為啥要用 C++ 來介紹下，不能用 Java 嗎?我再補充下，本文的測試結論，均來自于老外的文章，文章出處見開頭，其次，本文的后半部分的優化，都是基于一些系統調用，和 CPU 指令的優化，這些在 C++ 中實現起來方便一些，Java 只能走系統調用。

在最近過去的性能挑戰賽中，由于限定了不能使用 JNI，使得選手們只能將方案止步于循環展開方案，試想一下，如果允許走系統調用，加上比賽中字符串也基本是固定的長度，完全可以采用 SIMD 的 trick 方案，String 轉 Long 的速度會更快。

polardb優化點

實際上，在之前 polarDB 的比賽中，普哥就給我介紹過 bswap 的向量化方案，這也是為啥 Java 方案就是比 C++ 方案遜色的原因之一，C++ 在執行一些 CPU 指令集以及系統調用上，比 Java 方便很多。

如何看待這一系列的優化呢?從 std::stringstream 的 86.23 到 sima trick 方案的 0.75，這個優化的過程是令人興奮的，但我們也發現，越往后，越是用到一些底層的優化技巧，正如方案中的 trick 而言，適用性是有限的。也有一種聲音是在說：花費這么大精力去優化，為啥不去寫匯編呢?這又回到了“優化是萬惡之源”這個話題。在業務項目中，可能你不用過多關注 String 是如何轉換為 Long 和 Integer 的，可能 Integer.valueOf 和 Long.valueOf 就可以滿足你的訴求，但如果你是一個需要大數據解析系統，String 轉換是系統的瓶頸之一，相信本文的方案會給你一定的啟發。

另外對于 SIMD 這些方案，我想再多說一句。其實一些性能挑戰賽進行到最后，大家的整體方案其實都相差無幾，無非是參數差異，因為比賽場景通常不會太復雜，最后前幾名的差距，就是在一些非常小的細節上。正如 SIMA 提供的向量化運算等優化技巧，它就是可以幫助你比其他人快個幾百毫秒，甚至 1~2s。這時候你會感嘆，原來我跟大神的差距，就是在這些細節上。但反觀整個過程，似乎這些優化并不能幫助程序設計競賽發揮更大的能量，一個比賽如果只能依靠 CPU 優化來實現區分度，我覺得一定不是成功的。所以，對于主辦方而言，禁用掉一些類庫，其實有效的避免了內卷，于參賽者而言，算是一種減負了。希望以后的比賽也都朝著讓選手花更多精力去優化方案，而不是優化通用的細節上。

再回到 String 解析成 Long/Integer 的話題上。在實際使用時，大家也不用避諱繼續使用 Integer.valueOf 或者 Long.valueOf，大多數情況下，這不是系統的瓶頸。而如果你恰好在某些場景下遇到了 String 轉換的瓶頸，希望本文能夠幫到你。

責任編輯：武曉燕來源： Kirito的技術分享