順序隊列

順序隊列定義

隊列的底層是數(shù)組，我們常說的隊列其實就是順序隊列，其數(shù)據(jù)結構定義一般是：

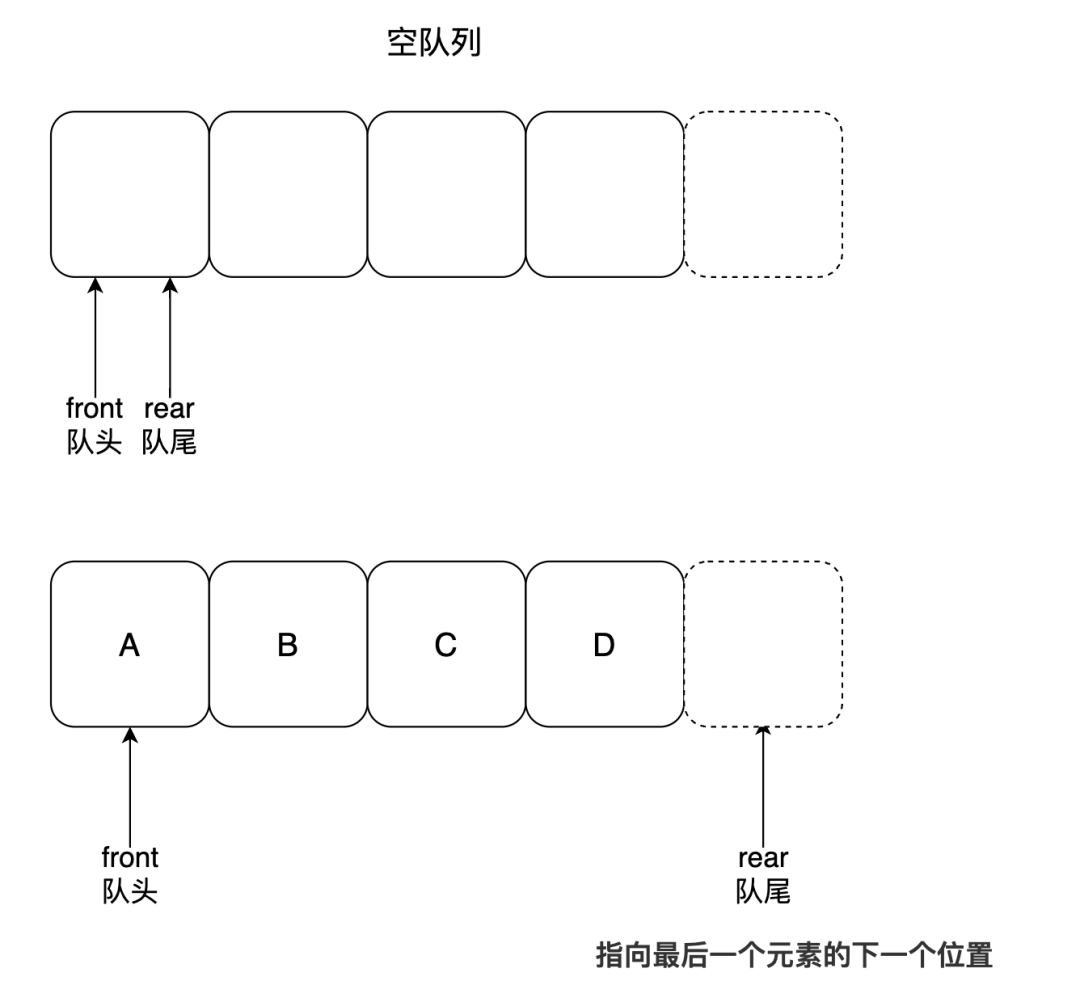
1. 隊頭指針指向數(shù)組第一個元素
2. 隊尾指針指向數(shù)組最后一個元素的下一個位置

為了避免當只有一個元素時，隊頭和隊尾重合使處理變得麻煩，所以這里引入了隊頭和隊尾兩個指針，假設 front 指針指向隊頭元素，rear 指針指向隊尾元素的下一個位置，這樣：

• 當 front == rear 時，表示這個隊列是空隊列
• 當 front == rear + 1 時，表示這個隊列中只有一個元素

示意圖如下：

圖片

眾所周知，隊列是先進先出的，那么進隊操作對應的步驟就是：先送值到隊尾，再將隊尾指針 +1

// 送值到隊尾
queue[rear] = x;
// 隊尾指針 +1
rear ++;

出隊操作：先取出隊頭元素，再將隊頭指針 +1

// 取出隊頭元素
x = queue[Q.front]
// 隊頭指針 +1
front ++;

假溢出問題

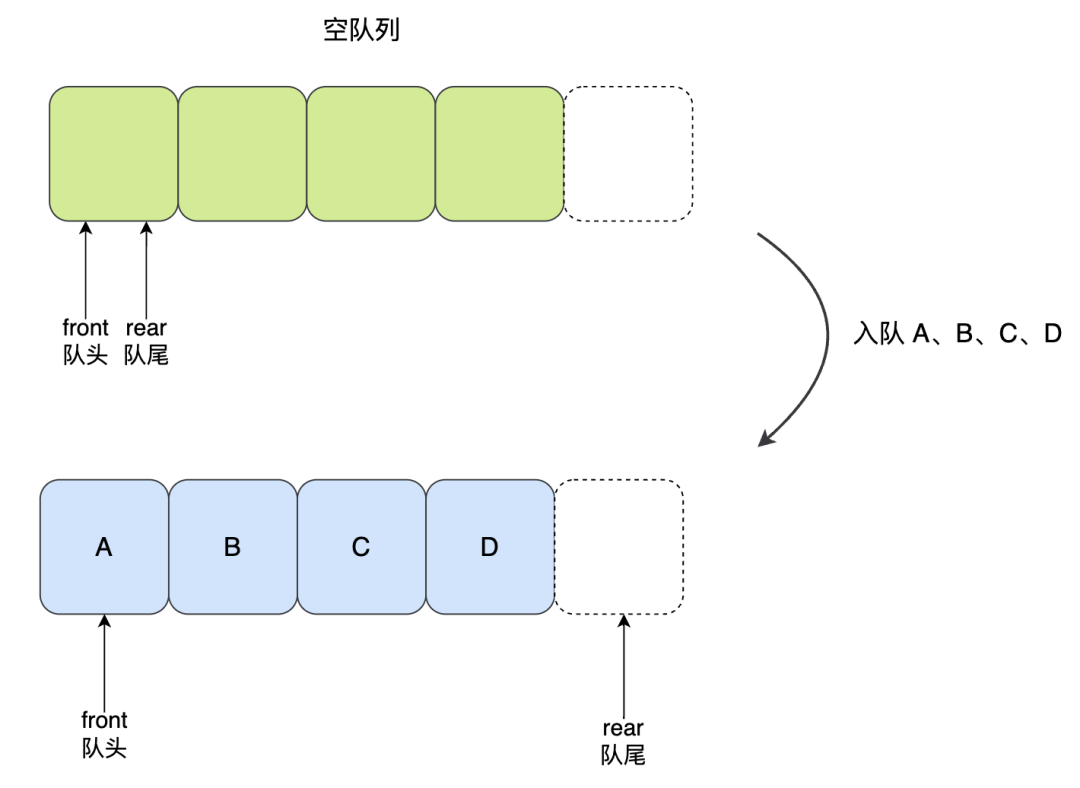
順序隊列存在假溢出問題 ，就是明明在隊列中仍然有可以存放元素的空間卻無法執(zhí)行入隊操作了，舉個例子：

隊列的大小是 5（數(shù)組容量為 5），一開始是空隊列，然后依次入隊了 A、B、C、D：

圖片

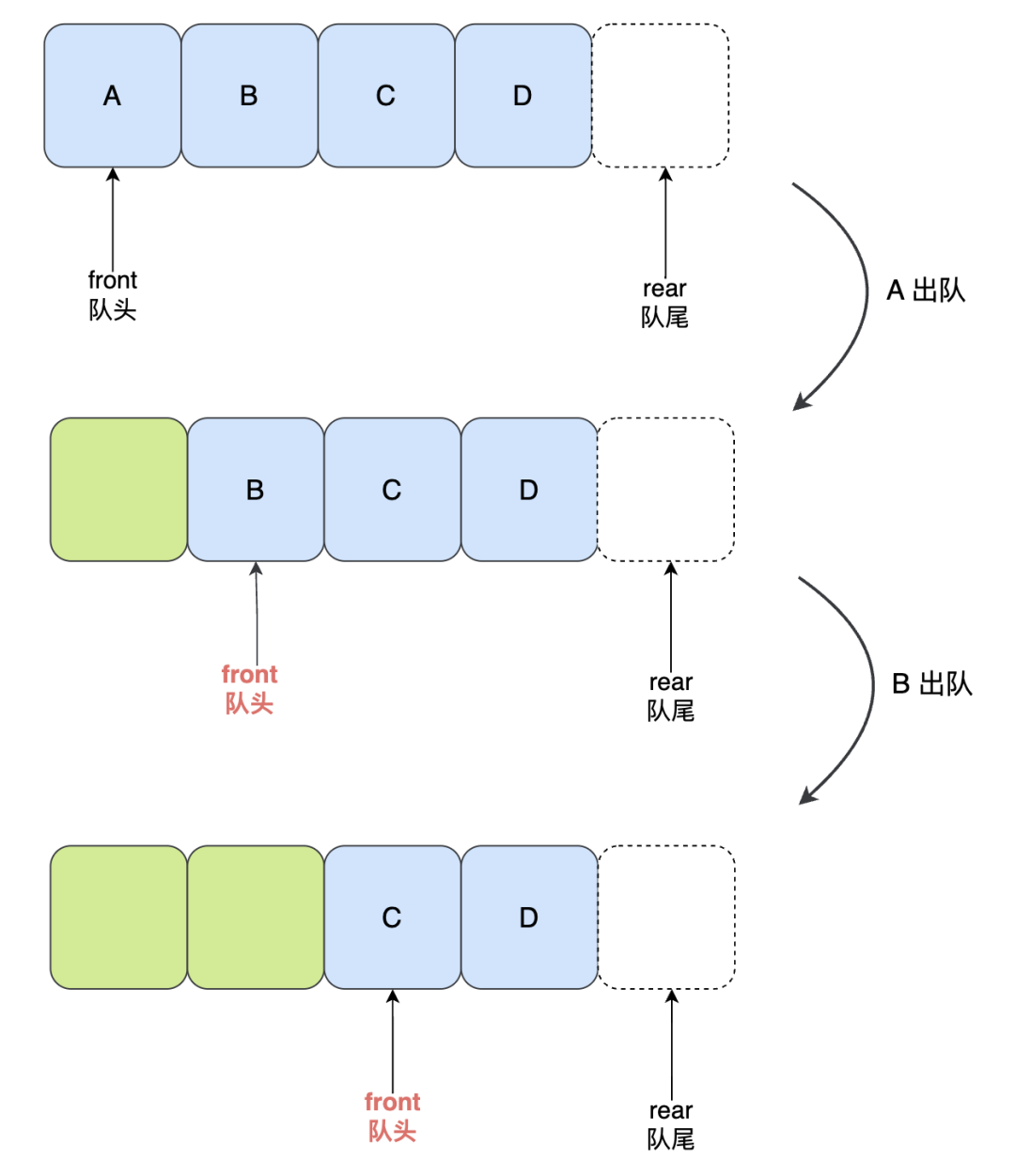
然后 A 出隊，B 出隊，相應的 front 指針會往后移動兩位：

圖片

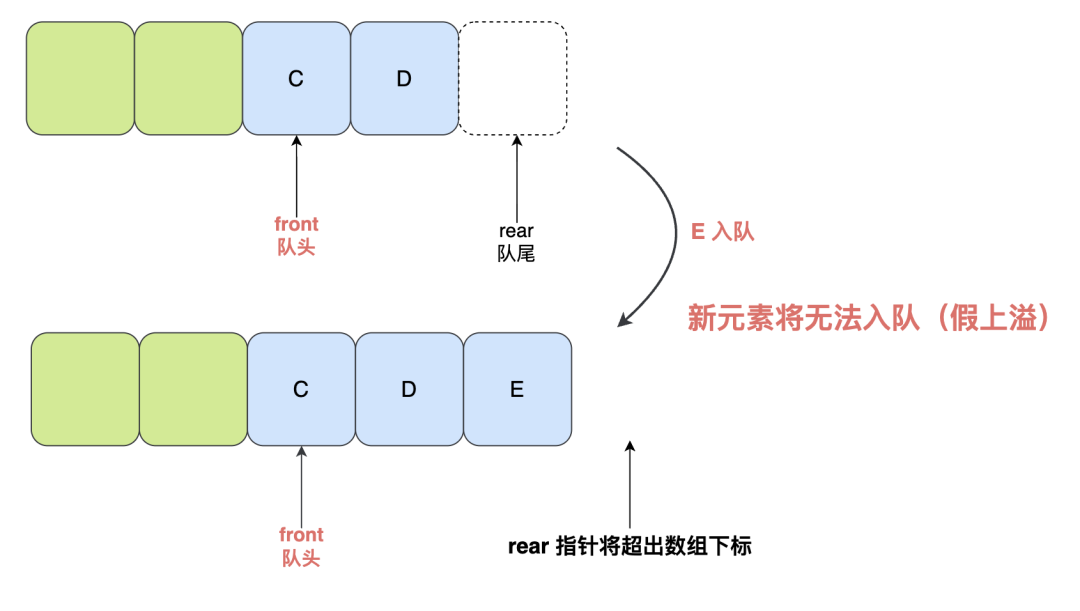
再入隊一個新元素 E，此時 front 指針不變，rear 指針需要 +1，已經超出了數(shù)組的下標范圍，就會導致新元素插入失敗：

圖片

明明隊列中還有空間，插入元素竟然會失敗？這就是一種假性上溢出現(xiàn)象。

如何解決這個問題呢，有三種：

1. 建立一個足夠大的存儲空間以避免溢出。這樣做空間使用率低，浪費存儲空間
2. 移動元素：每當出隊一個元素，就將移動隊列中所有的已有元素向隊頭移動一個位置。這樣做很明顯時間復雜度比較高，效率慢
3. 循環(huán)隊列：將隊頭和隊尾看作是一個首尾相接的循環(huán)隊列

因此，循環(huán)隊列是解決順序隊列假溢出問題的最佳選擇！

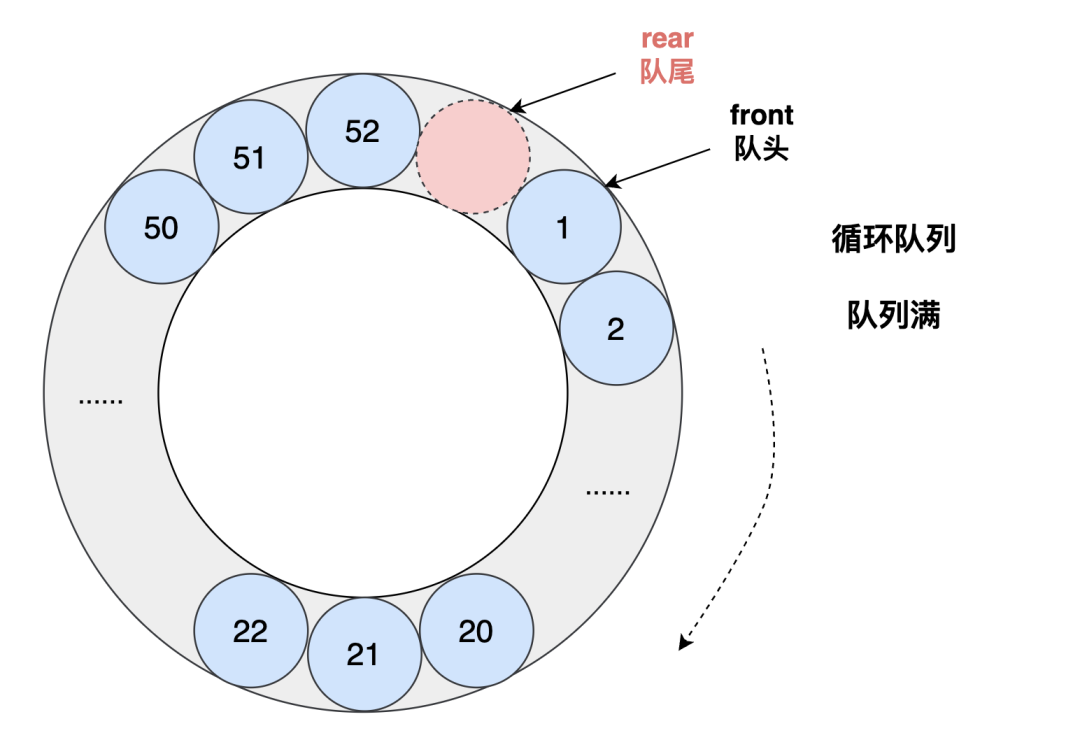
循環(huán)隊列

循環(huán)隊列的數(shù)據(jù)結構定義一般是：

1. 隊列長度固定，即隊列（數(shù)組）容量有限
2. 隊列的頭尾相接形成一個環(huán)，當隊尾到達數(shù)組的最后一個位置時，下一個位置是數(shù)組的第一個位置

具體實現(xiàn)步驟如下：

1. 定義一個數(shù)組和兩個指針：front 和 rear，分別表示隊頭和隊尾的位置。初始時（空隊列），隊頭和隊尾都指向數(shù)組的第一個位置，即 front = rear = 0。
2. 入隊時，首先檢查隊列是否已滿，如何判斷隊列滿？犧牲一個單元來區(qū)分隊空和隊滿：即 (rear + 1) % maxsize = front。如果滿了則返回錯誤，否則將元素添加到隊尾，即 queue[rear] = element，然后將 rear 指針向后移動一位，即 rear = (rear + 1) % capacity。
3. 出隊時，首先檢查隊列是否為空，**front == rear 就表示隊列空**。如果為空則返回錯誤，否則將隊頭元素取出并返回，即 element = queue[front]，然后將 front 指針向后移動一位，即 front = (front + 1) % capacity。
4. 在隊列的任何時刻，隊列中的元素數(shù)量為 (rear - front + capacity) % capacity

示意圖如下：

圖片

以下是一個基于數(shù)組實現(xiàn)循環(huán)隊列的 Java 代碼示例：

public class CircularQueue {
   // 存儲元素的數(shù)組
    private int[] data;
    private int front, rear;
   // 數(shù)組大小
    private int capacity;

    public CircularQueue(int k) {
        capacity = k;
        data = new int[capacity];
        front = 0;
        rear = 0;
    }

   // 入隊
    public boolean enqueue(int element) {
        if (isFull()) {
            return false;
        } else {
            data[rear] = element;
            rear = (rear + 1) % capacity;
            return true;
        }
    }
 
   // 出隊
    public boolean dequeue() {
        if (isEmpty()) {
            return false;
        } else {
            front = (front + 1) % capacity;
            return true;
        }
    }

    // 獲取隊頭元素
    public int front() {
        if (isEmpty()) {
            return -1;
        } else {
            return data[front];
        }
    }
  
   // 獲取隊尾元素
    public int rear() {
        if (isEmpty()) {
            return -1;
        } else {
            return data[(rear - 1 + capacity) % capacity];
        }
    }

   // 判斷隊列是否為空
    public boolean isEmpty() {
        return front == rear;
    }
 
   // 判斷隊列是否滿
    public boolean isFull() {
        return (rear + 1) % capacity == front;
    }
}

簡單總結就是：

• 初始/隊空：front = rear
• 出隊：front = (front + 1) % capacity (最大元素個數(shù))
• 進隊：rear = (rear + 1) % capacity
• 隊列長度：(rear - front + capacity) % capacity
• 隊滿（犧牲一個單元來區(qū)分隊空和隊滿 ）：(rear + 1) % capacity = front