機(jī)器學(xué)習(xí)之無監(jiān)督學(xué)習(xí):八大降維方法
之前我們總結(jié)了機(jī)器學(xué)習(xí)中常用的幾種回歸算法和分類算法。都屬于機(jī)器學(xué)習(xí)監(jiān)督學(xué)習(xí)算法。

今天,和大家分享一下機(jī)器學(xué)習(xí)之無監(jiān)督學(xué)習(xí)中的常見的降維方法。
我們可以怎樣發(fā)現(xiàn)一個(gè)數(shù)據(jù)集的底層結(jié)構(gòu)?我們可以怎樣最有用地對(duì)其進(jìn)行歸納和分組?我們可以怎樣以一種壓縮格式有效地表征數(shù)據(jù)?這都是無監(jiān)督學(xué)習(xí)的目標(biāo),之所以稱之為「無監(jiān)督」,是因?yàn)檫@是從無標(biāo)簽的數(shù)據(jù)開始學(xué)習(xí)的。
降維看上去很像壓縮。這是為了在盡可能保存相關(guān)的結(jié)構(gòu)的同時(shí)降低數(shù)據(jù)的復(fù)雜度。如果你有一張簡(jiǎn)單的 128×128×3 像素的圖像(長(zhǎng)×寬×RGB 值),那么數(shù)據(jù)就有 49152 維。如果你可以給這個(gè)圖像空間降維,同時(shí)又不毀掉圖像中太多有意義的內(nèi)容,那么你就很好地執(zhí)行了降維。
降維是一種常見的無監(jiān)督學(xué)習(xí)任務(wù),其目標(biāo)是將高維數(shù)據(jù)映射到低維空間,以減少數(shù)據(jù)的特征維度,同時(shí)保留數(shù)據(jù)的關(guān)鍵結(jié)構(gòu)和信息。通過降維,可以簡(jiǎn)化數(shù)據(jù)表示、減少存儲(chǔ)空間、降低計(jì)算復(fù)雜度,并幫助可視化和數(shù)據(jù)理解。
降維方法的選擇取決于數(shù)據(jù)的性質(zhì)、任務(wù)需求和算法的適用性。以下是一些常見的降維方法:
- 主成分分析(PCA)
- 獨(dú)立成分分析(ICA)
算法 t 分布-隨機(jī)鄰近嵌入(t-SNE) 線性判別分析(LDA) - 奇異值分解(SVD)
- 局部線性嵌入(LLE)
- 多維縮放(MDS)
- 等度量映射(Isomap)
1、主成分分析(PCA)
對(duì)于降維問題來說,目前最流行最常用的算法是一個(gè)叫做主成分分析法(Principal Components Analysis,PCA) 的算法,它可以用來做降維操作,也可以用來實(shí)現(xiàn)數(shù)據(jù)壓縮。
PCA 是一種統(tǒng)計(jì)分析、簡(jiǎn)化數(shù)據(jù)集的方法。它利用正交變換來對(duì)一系列可能相關(guān)的變量的觀測(cè)值進(jìn)行線性變換,從而投影為一系列線性不相關(guān)變量的值,這些不相關(guān)變量稱為主成分(Principal Components)。
具體地,主成分可以看做一個(gè)線性方程,其包含一系列線性系數(shù)來指示投影方向。PCA 對(duì)原始數(shù)據(jù)的正則化或預(yù)處理敏感(相對(duì)縮放)。
基本思想
(1)將坐標(biāo)軸中心移到數(shù)據(jù)的中心,然后旋轉(zhuǎn)坐標(biāo)軸,使得數(shù)據(jù)在 C1 軸上的方差最大,即全部 n 個(gè)數(shù)據(jù)個(gè)體在該方向上的投影最為分散。意味著更多的信息被保留下來。C1 成為第一主成分。
(2)C2 第二主成分:找一個(gè) C2,使得 C2 與 C1 的協(xié)方差(相關(guān)系數(shù))為 0,以免與 C1 信息重疊,并且使數(shù)據(jù)在該方向的方差盡量最大。
(3)以此類推,找到第三主成分,第四主成分……第 p 個(gè)主成分。p 個(gè)隨機(jī)變量可以有 p 個(gè)主成分。
主成分分析經(jīng)常用于減少數(shù)據(jù)集的維數(shù),同時(shí)保留數(shù)據(jù)集當(dāng)中對(duì)方差貢獻(xiàn)最大的特征。這是通過保留低維主成分,忽略高維主成分做到的。這樣低維成分往往能夠保留住數(shù)據(jù)的最重要部分。
2、獨(dú)立成分分析(ICA)算法
獨(dú)立成分分析(Independent Component Analysis, ICA)算法是一種基于統(tǒng)計(jì)學(xué)的降維算法,其目的是從多個(gè)隨機(jī)變量的混合信號(hào)中恢復(fù)出獨(dú)立的原始信號(hào),即通過對(duì)數(shù)據(jù)進(jìn)行線性變換,使得變換后的數(shù)據(jù)各個(gè)分量間盡可能地獨(dú)立。ICA 算法常用于信號(hào)處理、圖像處理、語音識(shí)別、腦電圖分析等領(lǐng)域。
ICA 和 PCA 的區(qū)別:
(1)PCA 是降維并提取不相關(guān)屬性,而 ICA 是降維并提取相互獨(dú)立的屬性(不相關(guān)不一定獨(dú)立,獨(dú)立一定不相關(guān)。不相關(guān)是指沒有線性關(guān)系,獨(dú)立是指沒有任何關(guān)系)。
(2)PCA 是提取出最能表示原始事物的特征,而 ICA 是使每個(gè)分量最大化獨(dú)立,便于發(fā)現(xiàn)隱藏因素
(3)PCA 的適用環(huán)境是數(shù)據(jù)為高斯分布,而 ICA 不適用于高斯分布的數(shù)據(jù)。
ICA算法的應(yīng)用
ICA算法在信號(hào)處理、圖像處理、語音識(shí)別等領(lǐng)域有廣泛應(yīng)用。以音頻信號(hào)處理為例,ICA可以將多個(gè)聲音信號(hào)混合在一起的信號(hào)分離開來。在語音識(shí)別領(lǐng)域,ICA可以將不同說話人的語音信號(hào)分離開來,方便后續(xù)的處理。
3、t 分布-隨機(jī)鄰近嵌入(t-SNE)
t-SNE(t-distributed stochastic neighbor embedding)算法是一種非線性降維算法,可以用于高維數(shù)據(jù)的可視化和聚類分析。t-SNE 算法通過將高維空間中的數(shù)據(jù)點(diǎn)映射到低維空間(通常是二維或三維空間)中,保留數(shù)據(jù)點(diǎn)之間的相對(duì)距離和分布,從而使得高維數(shù)據(jù)的結(jié)構(gòu)更加清晰可見。
t-SNE 算法的主要思想是通過 t 分布來描述低維空間中的點(diǎn)之間的相對(duì)距離,而通過高斯分布來描述高維空間中的點(diǎn)之間的相對(duì)距離。t-SNE 算法通過優(yōu)化 t 分布和高斯分布之間的 KL 散度來得到低維空間中的數(shù)據(jù)點(diǎn)位置。具體來說,算法首先隨機(jī)初始化低維空間中的點(diǎn)的位置,然后通過梯度下降來最小化高維空間中數(shù)據(jù)點(diǎn)之間的相對(duì)距離與低維空間中數(shù)據(jù)點(diǎn)之間的相對(duì)距離之間的KL散度,從而得到最終的低維表示。
t-SNE 算法的流程如下:
1.計(jì)算高維空間中的相對(duì)距離矩陣;
2.通過高斯分布來描述高維空間中的點(diǎn)之間的相對(duì)距離;
3.計(jì)算低維空間中的相對(duì)距離矩陣;
4.通過 t 分布來描述低維空間中的點(diǎn)之間的相對(duì)距離;
5.通過梯度下降來最小化高維空間中數(shù)據(jù)點(diǎn)之間的相對(duì)距離與低維空間中數(shù)據(jù)點(diǎn)之間的相對(duì)距離之間的KL散度;
6.重復(fù)第 5 步直至滿足收斂條件,得到最終的低維表示。
t-SNE 算法的應(yīng)用
t-SNE 算法可以用于可視化高維數(shù)據(jù),以便更好地理解數(shù)據(jù)之間的關(guān)系。下面的示例將展示如何使用 t-SNE 算法可視化手寫數(shù)字?jǐn)?shù)據(jù)集 MNIST 中的圖像。
4、線性判別分析(LDA)
線性判別分析(Linear Discriminant Analysis, LDA) 也是一種常用的線性降維方法,它與 PCA 不同的是,LDA 考慮了樣本的類別信息。LDA 試圖在降維的過程中保留類別之間的差異,以找到更具有判別性的特征。因此,LDA 在分類問題中特別有用。
LDA 的思想可以用一句話概括,就是“投影后類內(nèi)方差最小,類間方差最大”。通俗理解就是:將數(shù)據(jù)在低維度上進(jìn)行投影,投影后希望每一種類別數(shù)據(jù)的投影點(diǎn)盡可能的接近,而不同類別的數(shù)據(jù)的類別中心之間的距離盡可能的大。
之所以稱為線性判別分析,其實(shí)是因?yàn)槠渥钤缬迷诜诸惍?dāng)中:判別分析是尋找一種“分類規(guī)則”,即利用變量的函數(shù)(判別函數(shù))來描述(解釋)兩組或多組之間的區(qū)別。
5、奇異值分解(SVD)
在 2006 年,Netflix 曾經(jīng)舉辦了一個(gè)獎(jiǎng)金為 100 萬美元的推薦系統(tǒng)算法比賽,最后的獲獎(jiǎng)?wù)呔褪褂昧司仃嚪纸庵械拿餍牵浩娈愔捣纸猓⊿ingular-Value Decomposition,簡(jiǎn)稱SVD)。SVD 被廣泛應(yīng)用在推薦系統(tǒng)、圖像處理等領(lǐng)域,是一種數(shù)據(jù)降維的經(jīng)典方法。
奇異值分解是將矩陣分解為奇異向量和奇異值。通過奇異值分解,我們會(huì)得到一些與特征分解相同類型的信息。然而,奇異值分解有更廣泛的應(yīng)用。每一個(gè)實(shí)數(shù)矩陣都有一個(gè)奇異值分解,但不一定都有特征分解(例如非方陣矩陣)。
6、局部線性嵌入(LLE)
局部線性嵌入(Locally linear embedding,LLE)是一種非線性降維算法,它能夠使降維后的數(shù)據(jù)較好地保持原有 流形結(jié)構(gòu) 。LLE 可以說是流形學(xué)習(xí)方法最經(jīng)典的工作之一。很多后續(xù)的流形學(xué)習(xí)、降維方法都與 LLE 有密切聯(lián)系。
LLE 是非常重要的降維方法。和傳統(tǒng)的 PCA,LDA 等關(guān)注樣本方差的降維方法相比,LLE 關(guān)注于降維時(shí)保持樣本局部的線性特征,由于 LLE 在降維時(shí)保持了樣本的局部特征,它廣泛的用于圖像圖像識(shí)別,高維數(shù)據(jù)可視化等領(lǐng)域。
一個(gè)形象的流形降維過程如下圖。我們有一塊卷起來的布,我們希望將其展開到一個(gè)二維平面,我們希望展開后的布能夠在局部保持布結(jié)構(gòu)的特征,其實(shí)也就是將其展開的過程,就像兩個(gè)人將其拉開一樣。
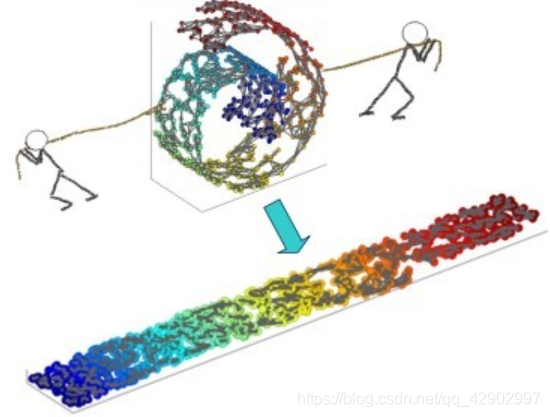
7、多維縮放(MDS)
多維縮放(Multiple Dimensional Scaling,簡(jiǎn)稱 MDS)是一種經(jīng)典的降維方法,要求原始空間中樣本之間的距離在低維空間中得以保持。
多維縮放,即對(duì)一組對(duì)象之間的距離或差異的視覺表示。“對(duì)象”可以是顏色,面孔,地圖坐標(biāo),各種真實(shí)存在的事物。除了將不同之處解釋為圖上的距離之外,MDS還可以作為高維數(shù)據(jù)的降維技術(shù)。簡(jiǎn)而言之。MDS 的主要目的是將這些差異保持在降維中。
MDS 算法思想很簡(jiǎn)單,一句話就是保持樣本在原空間和低維空間的距離不變。
8、等度量映射(Isomap)
Isomap(等度量映射)是在 MDS 算法的基礎(chǔ)上衍生出的一種非迭代的全局優(yōu)化算法,它是一種等距映射算法,也就是說降維后的點(diǎn),兩兩之間距離不變,這個(gè)距離是測(cè)地距離。
Isomap 方法是假設(shè)顯示情況中非線性數(shù)據(jù)的分布位于內(nèi)嵌歐式距離的流形體上,其中的關(guān)鍵在于數(shù)據(jù)點(diǎn)之間的距離用測(cè)地線距離來代替歐氏距離。
Isomap)的基本觀點(diǎn)同 MDS 較為類似,即從高維數(shù)據(jù)中找到任意兩個(gè)樣本點(diǎn)之間的“測(cè)地距離”,通過映射實(shí)現(xiàn)在低維空間中“測(cè)地距離”近似保持不變。
與 MDS 不同的是,MDS 計(jì)算的是歐氏距離,而 Isomap 計(jì)算的是“測(cè)地距離”。
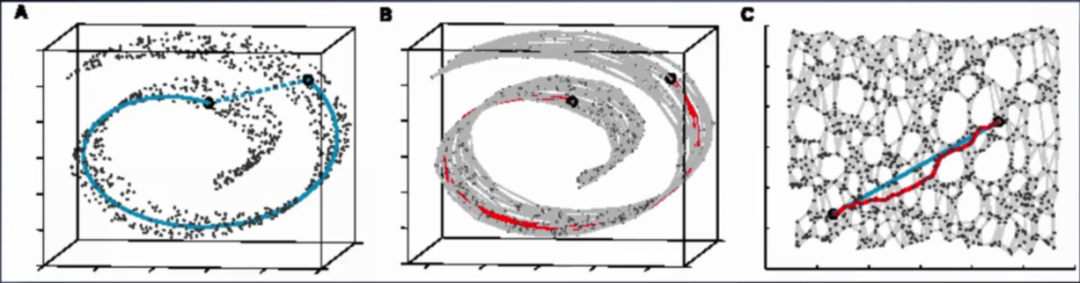
如上圖,“測(cè)地距離”即A中沿曲實(shí)線的兩點(diǎn)之間的距離,歐氏距離即如A中虛直線的兩點(diǎn)之間的直線距離。B圖即A的近鄰圖,C圖即B圖的低維映射結(jié)果,C圖中紅線為它的“測(cè)地距離”而藍(lán)線則為歐氏距離。
很明顯,Isomap中計(jì)算“測(cè)地距離”是非常重要的一步。如何計(jì)算“測(cè)地距離”呢?
我們可以利用流形在局部上與歐氏空間同胚這個(gè)性質(zhì),對(duì)每個(gè)點(diǎn)基于歐氏距離找出近鄰點(diǎn),然后建立一個(gè)近鄰圖。于是計(jì)算兩點(diǎn)之間測(cè)地距離的問題就變成了計(jì)算近鄰圖上兩點(diǎn)之間的最短路徑問題。而計(jì)算最短路徑可以使用 Dijkstra 算法或 Floyd 算法。得到任意兩點(diǎn)的距離之后就可以通過 MDS 算法來獲得樣本點(diǎn)在低維空間中的坐標(biāo)。




































