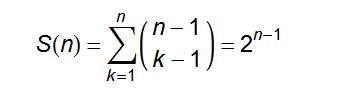問題

有這樣一個關于臺階和步數的題目：

假設A上臺階，一次可以跨1層，2層，3層.. 或m層，問A上n層臺階，有多少種走法？其中，m和n都是正整數，并且 m <= n

對臺階步數問題提出簡單分析，探索是否存在更優解的方案。

 

分析

這個問題等價于：

對于數n，有多少種方案讓小于n的數相加等于n，且這些數中的***數不超過m(m<=n) 

首先考慮m=n時情況

有多少種方案把n拆分成1...n份：

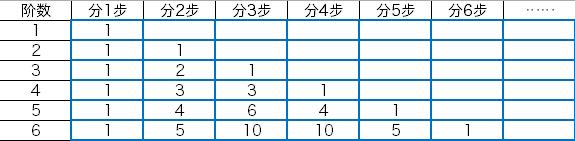
當n=2時，分1種{2}，分2種{1*2}

當n=3時，分1種{3}，分2種[1,2]的排列，分3種{1*3}

當n=4時，分1種{4}，分2種[1,3][2,2]的排列，分3種[1,1,2]的排列，分4種{1*4}

當n=5時，分1種{5}，分2種[1,4][2,3]的排列，分3種[1,1,3][1,2,2]的排列，分4種[1,1,1,2]的排列，分5種{1*5}

當n=6時，分1種{6}，分2種[1,5][2,4][3,3]的排列，分3種[1,1,4][1,2,3][2,2,2]的排列，分4種[1,1,1,3][1,1,2,2]的排列，分5種[1,1,1,1,2]的排列，分6種1*6

……

于是每一步分法都是一個將整數n的進行有序k分拆問題。

根據組合數學定理：正整數n的有序k分拆的個數等于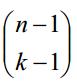。即(n-1)選(k-1)的組合數。

這正是楊輝三角的第n行第k項的通項：

于是，可以得到：

那么 k→1...n 總方案數(即為n從1拆分到n拆分的和的函數，用S(n)記號表示)

   （根據楊輝三角性質）

 

考慮1<m<n的情況：

(非常抱歉因疏于嚴謹上一版中該部分推測有誤，經查證后給出準確方法。特別感謝 @張晉坤 @顧健 等同學的斧正。)

當m<n時，該問題可以描述為，設k施一個給定的正整數，設h_k(n)表示將正整數n拆分分部量只含1,2,3...k的有序分拆數。該問題符合廣義斐波那契數定義，則h_k(n)滿足：

當n<=k時，h_k(n)=2^n-1

當n>k>=2時，h_k(n)=h_k(n-1)+h_k(n-2)+...+h_k(n-k)

因為n<=k時，正整數n拆成分部量只含1,2..k的有序分拆數，就是n的有序分拆數，而n得有序分拆數就是2^n-1。

所以，根據定理寫出了此迭代的循環版本，如下面的wideFib方法。 

總結

以上總結，可以用一分段函數來描述這個問題的通解： 

當m=n時復雜度為O(1)

當m<n時復雜度為O(nm+n)，雖然未能達到線性復雜度，但也能看出具有更小的常數階。

所以有一定程度的優化改善。

 

示例

利用上面的結論，給出如下代碼：

//java  
    
    static long stepsOfTerrace(int n, int m) {  
        if (m > n || n < 2)  
            throw new IllegalArgumentException();  
        if (m == n)  
            return (long) Math.pow(2, n - 1);  
        else if (m > 1)  
            return wideFib(n , m);  
        else 
            return n;  
    }  
 
    static long wideFib(int n, int k) {  
        long[] steps = new long[n];  
        for (int i = 1; i <= n - 1; i++) {  
            if (i <= k)    // hk(k)之前序列=2^n-1  
                steps[i] = (int) Math.pow(2, i - 1);  
            else    // 之后按照廣義斐波那契計算  
                for (int j = i - 1; j >= i - k; j--)  
                    steps[i] += steps[j];  
        }  
        long sum = 0;  
        for (int i = n - k; i <= n - 1; i++)  
            sum += steps[i];  
        return sum;  
    }   

原文鏈接：http://my.oschina.net/spance/blog/229477