手把手:用Python搭建機器學習模型預測黃金價格
編譯:小明同學君、吳雙、Yawei xia
新年總是跟黃金密不可分。新年第一天,讓我們嘗試用python搭建一個機器學習線性回歸模型,預測金價!
自古以來,黃金一直作為貨幣而存在,就是在今天,黃金也具有非常高的儲藏價值,那么有沒有可能預測出黃金價格的變化趨勢呢?
答案是肯定的,讓我們使用機器學習中的回歸算法來預測世界上貴重金屬之一,黃金的價格吧。
我們將建立一個機器學習線性回歸模型,它將從黃金ETF (GLD)的歷史價格中獲取信息,并返回黃金ETF價格在第二天的預測值。
GLD 是最大的以黃金進行直接投資的ETF交易基金。
在python的開發環境下用機器學習預測黃金價格的步驟:
- 導入Python庫并讀取黃金ETF 的數據
- 定義解釋變量
- 將數據切分為模型訓練數據集和測試數據集
- 建立線性回歸模型
- 預測黃金ETF的價格
導入Python庫并讀取黃金 ETF 的數據
首先:導入實現此策略所需的所有必要的庫(LinearRegression,pandas,numpy,matplotlib,seaborn和fix_yahoo_finance)
- # LinearRegression is a machine learning library for linear regression
- from sklearn.linear_model import LinearRegression
- # pandas and numpy are used for data manipulation
- import pandas as pd
- import numpy as np
- # matplotlib and seaborn are used for plotting graphs
- import matplotlib.pyplot as plt
- import seaborn
- # fix_yahoo_finance is used to fetch data import f
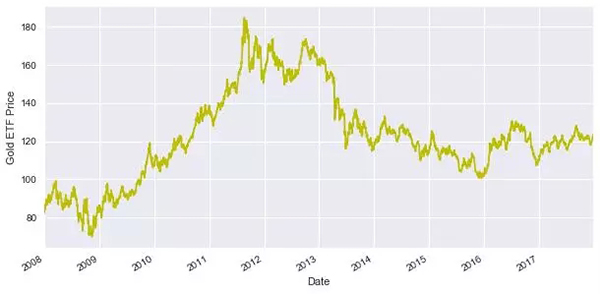
然后我們讀取過去10年間每天黃金ETF的價格數據,并將數據儲存在Df中。我們移除那些不相關的變量并使用dropna函數刪除NaN值。然后我們繪制出黃金ETF的收盤價格。
- # Read data
- Df = yf.download('GLD','2008-01-01','2017-12-31')
- # Only keep close columns
- DfDf=Df[['Close']]
- # Drop rows with missing values
- DfDf= Df.dropna()
- # Plot the closing price of GLD
- Df.Close.plot(figsize=(10,5))
- plt.ylabel("Gold ETF Prices")
- plt.show()
輸出
定義解釋變量
解釋變量是被用來決定第二天黃金ETF價格數值的變量。簡單地說,就是我們用來預測黃金ETF價格的特征值。本例中的解釋變量是過去3天和9天的價格移動平均值。我們使用dropna()函數刪除NaN值,并將特征變量存于X中。
然而,你還可以在X中放入更多你認為對于預測黃金ETF價格有用的變量。這些變量可以是技術指標,也可以是另一種ETF的價格(如黃金礦工ETF (簡稱GDX)或石油ETF(簡稱USO))或美國經濟數據。
- Df['S_3'] = Df['Close'].shift(1).rolling(window=3).mean()
- Df['S_9']= Df['Close'].shift(1).rolling(window=9).mean()
- DfDf= Df.dropna()
- X = Df[['S_3','S_9']]
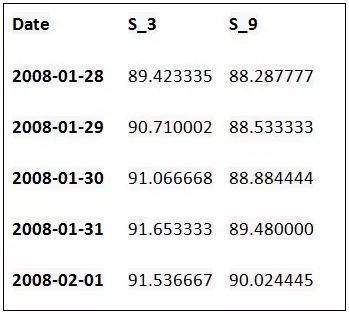
- X.head()
輸出
定義因變量
同樣,因變量是取決于解釋變量的“被解釋變量”。簡單地說,在這里就是我們試圖預測的黃金ETF價格。我們將黃金ETF的價格賦值為y。
- y = Df['Close']
- y.head()
輸出
- 2008-02-08 91.000000
- 2008-02-11 91.330002
- 2008-02-12 89.330002
- 2008-02-13 89.440002
- 2008-02-14 89.709999
- Name: Close, dtype: float64
將數據切分為模型訓練數據集和測試數據集
在此步驟中,我們將預測變量(解釋變量)數據和輸出(因變量)數據拆分為訓練數據集和測試數據集。訓練數據用于建立線性回歸模型,將輸入與預期輸出配對。測試數據用于評估模型的訓練效果。
- 前80%的數據用于訓練模型,其余的數據用來測試模型。
- X_train 和y_train是訓練數據集。
- X_test & y_test是測試數據集。
- t=.8
- t = int(t*len(Df))
- # Train dataset
- XX_train = X[:t]
- yy_train = y[:t]
- # Test dataset
- XX_test = X[t:]
- yy_test = y[t:]
建立線性回歸模型
接下來我們將建立一個線性回歸模型。什么是線性回歸呢?
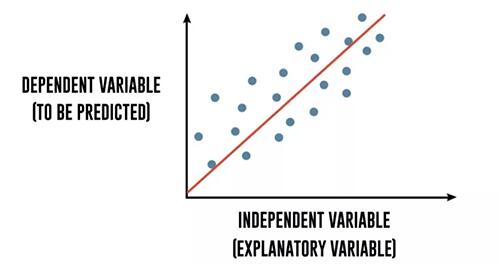
如果我們試圖捕捉可以最優解釋Y觀測值的X變量和Y變量之間的數學關系,我們將在X的觀測值形成的散點圖中去擬合一條線,那么這條線,也就是x和y之間的方程就被稱為線性回歸分析。
再進一步地說,回歸解釋了因變量在自變量上的變化。因變量y是你想要預測的變量。自變量x是用來預測因變量的解釋變量。下面的回歸方程描述了這種關系:
- Y = m1 * X1 + m2 * X2 + CGold ETF price = m1 * 3 days moving average + m2 * 15 days moving average + c
然后我們利用擬合方法來擬合自變量和因變量(x和y),從而生成系數和回歸常數。
- linear = LinearRegression().fit(X_train,y_train)
- print "Gold ETF Price =", round(linear.coef_[0],2), \
- "* 3 Days Moving Average", round(linear.coef_[1],2), \
- "* 9 Days Moving Average +", round(linear.intercept_,2)
輸出
黃金ETF價格=1.2×3天的移動平均價-0.2×9天的移動平均價+0.39
預測黃金ETF的價格
現在,是時候檢查模型是否在測試數據集中有效了。我們使用由訓練數據集建立的線性模型來預測黃金ETF的價格。預測模型可以得到給定解釋變量X后相應的黃金ETF價格(y)。
- predicted_price = linear.predict(X_test)
- predicted_price = pd.DataFrame(predicted_price,index=y_test.index,columns = ['price'])
- predicted_price.plot(figsize=(10,5))
- y_test.plot()
- plt.legend(['predicted_price','actual_price'])
- plt.ylabel("Gold ETF Price")
- plt.show()
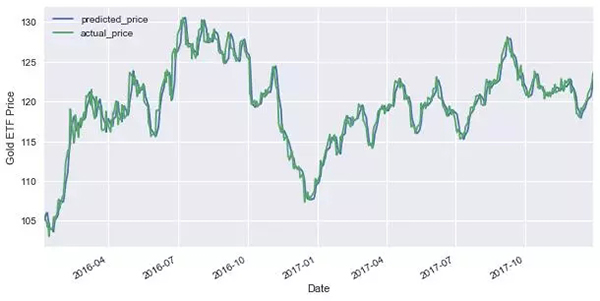
輸出
圖表顯示了黃金ETF價格的預測值和實際值(藍線是預測值,綠線是實際值)。
現在,讓我們使用score()函數來計算模型的擬合優度。
- r2_score = linear.score(X[t:],y[t:])*100
- float("{0:.2f}".format(r2_score))
可以看出,模型的R²是95.81%。R²總是在0到100%之間。接近100%的分數表明該模型能很好地解釋黃金ETF的價格。
祝賀你,你剛剛學會了一種基本而又強大的機器學習技巧。
原文鏈接:
https://www.quantinsti.com/blog/gold-price-prediction-using-machine-learning-python/
【本文是51CTO專欄機構大數據文摘的原創譯文,微信公眾號“大數據文摘( id: BigDataDigest)”】