隨著云計(jì)算和人工智能的發(fā)展，數(shù)據(jù)科學(xué)這門新的綜合學(xué)科被越來越多的人所熟知，業(yè)界也普遍看好其在未來的發(fā)展前景。體現(xiàn)在就業(yè)市場上，與這個(gè)行業(yè)相關(guān)的數(shù)據(jù)科學(xué)家和數(shù)據(jù)工程師成為了“21世紀(jì)最吸引人的職業(yè)”。 就像“一千個(gè)人眼里有一千個(gè)哈姆雷特”一樣，對于什么是數(shù)據(jù)科學(xué)也有很多種不同的解讀，并由此衍生出很多相關(guān)概念，比如數(shù)據(jù)驅(qū)動(data driven)、大數(shù)據(jù)(big data)、分布式計(jì)算(distributed computing)等。但這些概念都沒能全面地描述數(shù)據(jù)科學(xué)的內(nèi)涵，本文將從目標(biāo)、挑戰(zhàn)和門派三個(gè)方面來闡述什么是數(shù)據(jù)科學(xué)。

一、目標(biāo)

數(shù)據(jù)科學(xué)是一門最近大火的新興學(xué)科。這門學(xué)科的目標(biāo)十分簡單，就是如何從實(shí)際的生活中提取出數(shù)據(jù)，然后利用計(jì)算機(jī)的運(yùn)算能力和模型算法從這些數(shù)據(jù)中找出一些有價(jià)值的內(nèi)容，為商業(yè)決策提供支持。

傳統(tǒng)的數(shù)據(jù)分析手段是所謂的商業(yè)智能(business intelligence)。這種方法通常將數(shù)據(jù)按不同的維度交叉分組，并在此基礎(chǔ)上，利用統(tǒng)計(jì)方法分析每個(gè)組別里的信息。比如商業(yè)智能中最常見的問題是：“過去3個(gè)月，通過搜索引擎進(jìn)入網(wǎng)站并成功完成注冊的新用戶里，年齡分布情況如何?若將上面的用戶群按年齡段分組，各組中有多大比例的用戶在完成注冊后，完成了至少一次消費(fèi)?”

這樣的分析是非常有用的，能揭示一些數(shù)據(jù)的直觀信息。但這樣的方法如同盲人摸象，只能告訴我們數(shù)據(jù)在某個(gè)局部的情況，而不能給出數(shù)據(jù)的全貌。而且對于某些問題，這樣的結(jié)果顯得有些不夠用。比如用戶注冊之后完成消費(fèi)的比例與哪些因素相關(guān)?又比如對于某個(gè)客戶，他對某一產(chǎn)品的估計(jì)是多少?在這些場景下，我們就需要更加精細(xì)的數(shù)據(jù)分析工具—機(jī)器學(xué)習(xí)和統(tǒng)計(jì)模型。這些內(nèi)容正是數(shù)據(jù)科學(xué)的核心內(nèi)容。 

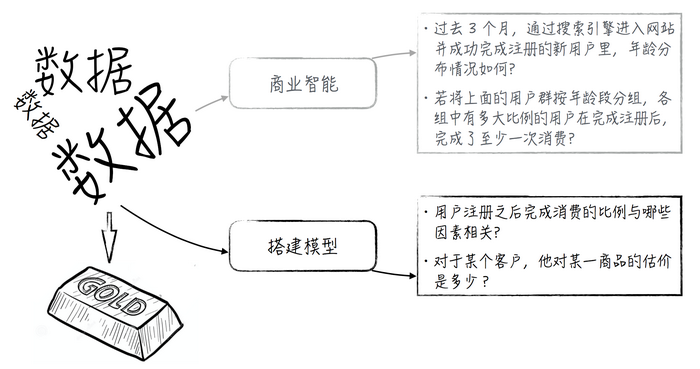
圖1

二、挑戰(zhàn)

在數(shù)據(jù)科學(xué)實(shí)踐中，我們將使用較為復(fù)雜的機(jī)器學(xué)習(xí)或統(tǒng)計(jì)模型對數(shù)據(jù)做精細(xì)化的分析和預(yù)測。這在工程實(shí)現(xiàn)和模型搭建兩方面都提出了挑戰(zhàn)，如圖2所示。

工程實(shí)現(xiàn)的挑戰(zhàn)

數(shù)據(jù)科學(xué)在工程上的挑戰(zhàn)可以大致分為3類：特征提取、矩陣運(yùn)算和分布式機(jī)器學(xué)習(xí)。

(1)一個(gè)建模項(xiàng)目的成功在很大程度上依賴于建模前期的特征提取。它包含數(shù)據(jù)清洗、數(shù)據(jù)整合、變量歸一化等。經(jīng)過處理后，原本攪作一團(tuán)的原始數(shù)據(jù)將被轉(zhuǎn)換為能被模型使用的特征。這些工作需要大量的自動化程序來處理，特別是面對大數(shù)據(jù)時(shí)，因?yàn)檫@些大數(shù)據(jù)無法靠“人眼”來檢查。在一個(gè)典型的建模項(xiàng)目中，這部分花費(fèi)的時(shí)間遠(yuǎn)遠(yuǎn)大于選擇和編寫模型算法的時(shí)間。

(2)對于一個(gè)復(fù)雜的數(shù)學(xué)模型，計(jì)算機(jī)通常需要使用類似隨機(jī)梯度下降法的***化算法來估算它的模型參數(shù)。這個(gè)過程需要大量的循環(huán)，才能使參數(shù)到達(dá)收斂值附近。因此即使面對的是很小的數(shù)據(jù)集，復(fù)雜的模型也需要很長時(shí)間才能得到正確的參數(shù)估計(jì)。而且模型在結(jié)構(gòu)上越復(fù)雜，需要估計(jì)的參數(shù)也就越多。對這些大量的模型參數(shù)同時(shí)做更新，在數(shù)學(xué)上對應(yīng)著矩陣運(yùn)算。但傳統(tǒng)的CPU架構(gòu)并不擅長做這樣的運(yùn)算，這導(dǎo)致模型訓(xùn)練需要耗費(fèi)大量的時(shí)間。為了提高模型的訓(xùn)練速度，需要將相應(yīng)的矩陣運(yùn)算(模型參數(shù)的估算過程)移植到GPU或者特制的計(jì)算芯片上，比如TPU。

(3)近年來，隨著分布式系統(tǒng)的流行和普及，存儲海量數(shù)據(jù)成為了業(yè)界的標(biāo)配。為了能在這海量的數(shù)據(jù)上使用復(fù)雜模型，需要將原本在一臺機(jī)器上運(yùn)行的模型算法改寫成能在多臺機(jī)器上并行運(yùn)行，這也是分布式機(jī)器學(xué)習(xí)的核心內(nèi)容。 

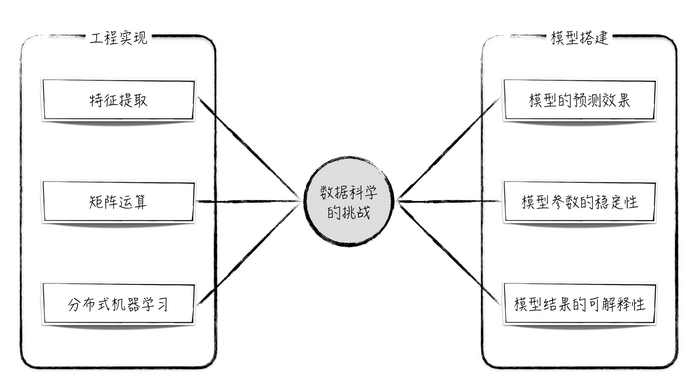
圖2模型搭建的挑戰(zhàn)

數(shù)據(jù)科學(xué)對模型搭建的要求也可以總結(jié)為3點(diǎn)：模型預(yù)測效果好、模型參數(shù)是穩(wěn)定且“正確”的、模型結(jié)果容易解釋。

(1)模型的預(yù)測效果好，這是數(shù)據(jù)科學(xué)成功的關(guān)鍵。而一個(gè)模型的預(yù)測效果取決于它的假設(shè)是否被滿足。從數(shù)學(xué)上來看，任何一個(gè)模型除去假設(shè)部分，它的其他推導(dǎo)都是嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)演算，是無懈可擊的。因此模型假設(shè)就像模型的阿喀琉斯之踵，是它唯一的薄弱環(huán)節(jié)。當(dāng)問題場景或數(shù)據(jù)滿足模型假設(shè)時(shí)，模型的效果一定不會差，反之，則預(yù)測效果就無法保證了。但在實(shí)際生產(chǎn)中，針對一個(gè)具體的問題，幾乎不可能找到一個(gè)模型，它的假設(shè)被***地滿足。這時(shí)就需要避重就輕，通過特征提取等手段，盡量避免違反那些對結(jié)果影響很大的假設(shè)。這就是為什么說“所有模型都是錯(cuò)的，但是，其中有一些是有用的”。

(2)除了被用來對未知數(shù)據(jù)做預(yù)測外，模型另一個(gè)重要的功能就是對已有數(shù)據(jù)做分析，比如哪個(gè)變量對結(jié)果的影響***或者某個(gè)變量對結(jié)果到底是正向影響還是負(fù)向影響等。這些分析結(jié)果在很大程度上依賴于模型參數(shù)的估計(jì)值，后者的準(zhǔn)確與否直接決定分析結(jié)果的質(zhì)量。但問題是，模型參數(shù)的估計(jì)值是不太“可靠”的。例如從訓(xùn)練數(shù)據(jù)中隨機(jī)抽取兩個(gè)不完全一樣的數(shù)據(jù)子集A和B，然后用這兩個(gè)數(shù)據(jù)集分別訓(xùn)練同一個(gè)模型。得到的參數(shù)估計(jì)值幾乎不可能完全一樣。從數(shù)學(xué)的角度來看，這說明模型參數(shù)的估計(jì)值其實(shí)是一個(gè)隨機(jī)變量，具體的值取決于訓(xùn)練模型時(shí)使用的數(shù)據(jù)。于是我們要求這些估計(jì)值是“正確”的：圍繞參數(shù)真實(shí)值上下波動(也就是說它們的期望等于參數(shù)真實(shí)值)。我們還要求這些估計(jì)值是穩(wěn)定的：波動的幅度不能太大(也就是說它們的方法比較小)。這樣就可以把參數(shù)估計(jì)值的“不可靠性”控制在可接受的范圍內(nèi)。

(3)數(shù)據(jù)科學(xué)家將模型搭建好，并不是一個(gè)數(shù)據(jù)科學(xué)項(xiàng)目的終點(diǎn)。為了充分發(fā)揮數(shù)據(jù)的價(jià)值，需要將模型結(jié)果應(yīng)用到實(shí)際的生產(chǎn)中，比如為手機(jī)銀行APP架設(shè)實(shí)時(shí)反欺詐系統(tǒng)，或者將利用新搭建的車禍風(fēng)險(xiǎn)模型為汽車保險(xiǎn)定價(jià)等。參與這個(gè)過程的不僅有懂模型的數(shù)據(jù)科學(xué)家，還有更多非技術(shù)的業(yè)務(wù)人員。而后者往往是使用模型的主力，比如根據(jù)反欺詐系統(tǒng)的結(jié)果，對可疑用戶進(jìn)行人工審核，又或者向客戶解釋為什么他的車險(xiǎn)比別人貴。為了幫助他們更好地理解模型結(jié)果，需要將復(fù)雜深奧的模型翻譯成直觀的普通語言。這要求模型是能被解釋的，而且是容易被解釋的。

三、兩大門派

和武俠世界里有少林和武當(dāng)兩大門派一樣，數(shù)據(jù)科學(xué)領(lǐng)域也有兩個(gè)不同的學(xué)派：以統(tǒng)計(jì)分析為基礎(chǔ)的統(tǒng)計(jì)學(xué)派，以及以機(jī)器學(xué)習(xí)為基礎(chǔ)的人工智能派。雖然這兩個(gè)學(xué)派的目的都是從數(shù)據(jù)中挖掘價(jià)值，但彼此“都不服氣”。注重模型預(yù)測效果的人工智能派認(rèn)為統(tǒng)計(jì)學(xué)派“固步自封”，研究和使用的模型都只是一些線性模型，太過簡單，根本無法處理復(fù)雜的現(xiàn)實(shí)數(shù)據(jù)。而注重假設(shè)和模型解釋的統(tǒng)計(jì)學(xué)派則認(rèn)為人工智能派搭建的模型缺乏理論依據(jù)、無法解釋，很難幫助我們通過模型去理解數(shù)據(jù)。

在學(xué)術(shù)上，通常將統(tǒng)計(jì)學(xué)派的模型稱為數(shù)據(jù)模型(data model)，將人工智能派的模型稱為算法模型(algorithm model)，如圖3所示。

數(shù)據(jù)模型的建模思路是假設(shè)數(shù)據(jù)的產(chǎn)生過程是已知的(或者是可以假設(shè)的)，可以通過模型去理解整個(gè)過程。因此，這類模型通常具有很好的可解釋性，分析其穩(wěn)定性的數(shù)學(xué)工具也很多，能很好地滿足上面提到的后兩點(diǎn)。但是在實(shí)際生產(chǎn)中，這些模型的預(yù)測效果并不好，或者更準(zhǔn)確地說，單獨(dú)使用時(shí)，預(yù)測效果并不理想。 

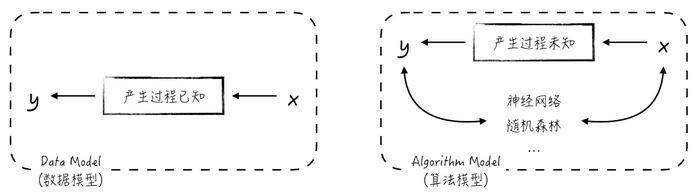
圖3算法模型，也就是人工智能的核心內(nèi)容，它們假設(shè)數(shù)據(jù)的產(chǎn)生過程是復(fù)雜且未知的。建模的目的是盡可能地從結(jié)構(gòu)上“模仿”數(shù)據(jù)的產(chǎn)生過程，從而達(dá)到較好的預(yù)測效果。但代價(jià)是模型的可解釋性很差，而且模型穩(wěn)定性的分析方法也不多。

事實(shí)上，統(tǒng)計(jì)學(xué)和機(jī)器學(xué)習(xí)在某些方面具有極好的互補(bǔ)性。因此在實(shí)際的生產(chǎn)中，為了將一個(gè)數(shù)據(jù)科學(xué)項(xiàng)目做得盡可能***，我們需要將這兩種思路結(jié)合起來使用。比如使用機(jī)器學(xué)習(xí)的模型對數(shù)據(jù)建模，然后借鑒數(shù)據(jù)模型的分析工具，分析模型的穩(wěn)定性和給出模型結(jié)果的直觀解釋。

四、模型幻覺

雖然數(shù)據(jù)科學(xué)領(lǐng)域兩大門派的模型很多，但它們都特別依賴所使用的數(shù)據(jù)。但是數(shù)據(jù)就***可靠嗎?下面就來看兩個(gè)數(shù)據(jù)“說謊”的例子。

如圖4所示，我們將某APP每月的用戶注冊數(shù)表示在圖中。圖4a給人的直觀印象是每月的安裝數(shù)是大致差不多的，沒有明顯的增長。而圖4b給人不同的印象，從3月份開始，用戶注冊數(shù)大幅度增長。但其實(shí)兩幅圖的數(shù)據(jù)是一模一樣的，給人不同的感覺是因?yàn)閳D4a中縱軸的起點(diǎn)是0，而且使用了對數(shù)尺度;而圖4b的縱軸是從17 000開始的，而且使用的是線性尺度。 

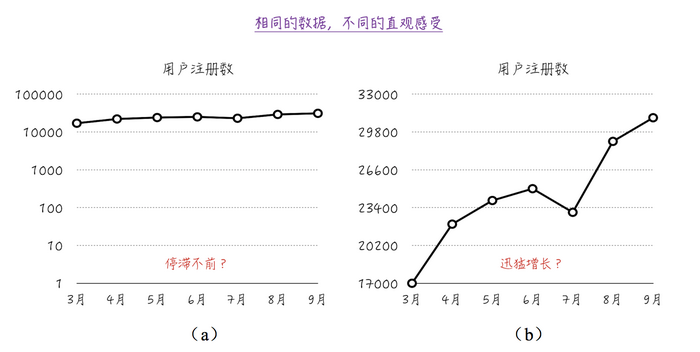
圖4讀者可能會覺得上面這個(gè)例子太過簡單了，只需要使用一些簡單的統(tǒng)計(jì)指標(biāo)，比如平均值或每個(gè)月的增長率，就可以避免錯(cuò)誤的結(jié)論。那么下面來看一個(gè)復(fù)雜一點(diǎn)的例子。

當(dāng)?shù)玫饺鐖D5所示的兩組數(shù)據(jù)時(shí)，我們應(yīng)該如何用模型去描述數(shù)據(jù)的變化規(guī)律呢?

對于圖5a，數(shù)據(jù)的圖形有點(diǎn)像拋物線，因此選擇二次多項(xiàng)式擬合是一個(gè)比較合理的選擇。于是假設(shè)模型的形式為y = (x - a)(x - b)。然后使用數(shù)據(jù)去估計(jì)模型中的未知參數(shù)a, b。得到的結(jié)果還不錯(cuò)，模型的預(yù)測值與真實(shí)值的差異并不大。 

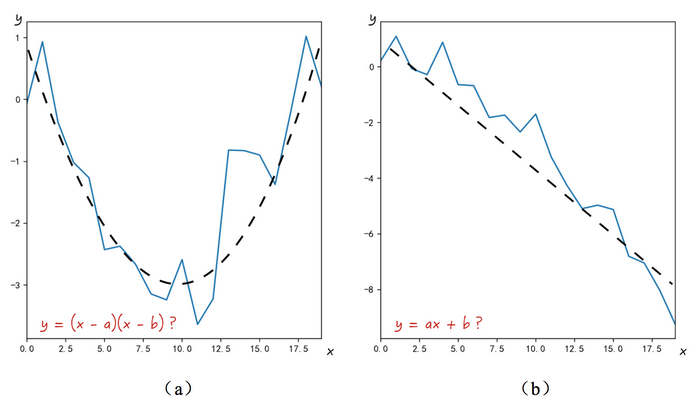
圖5對于圖5b，數(shù)據(jù)之間有明顯的線性關(guān)系，所以使用線性回歸對其建模，即y = ax + b。與上面類似，得到的模型結(jié)果也不錯(cuò)。

根據(jù)上面的分析結(jié)果，可以得出如下的結(jié)論，圖5a中的x與y之間是二次函數(shù)關(guān)系，而圖5b的x與y之間是線性關(guān)系。但其實(shí)兩幅圖中的變量y都是與x無關(guān)的隨機(jī)變量，只是因?yàn)橛^察窗口較小，收集的數(shù)據(jù)樣本太少，讓我們誤以為它們之間存在某種關(guān)系。如果增大觀察窗口，收集更多的數(shù)據(jù)，則可以得到完全不同的結(jié)論。如圖6所示，如果將收集的樣本數(shù)從20增加到200，會發(fā)現(xiàn)圖6a中的數(shù)據(jù)圖形更像是一個(gè)向下開口的拋物線，這與圖5a中的結(jié)論完全相反。而圖6b中也不再是向下的直線，而與開口向上的拋物線更加相似。 

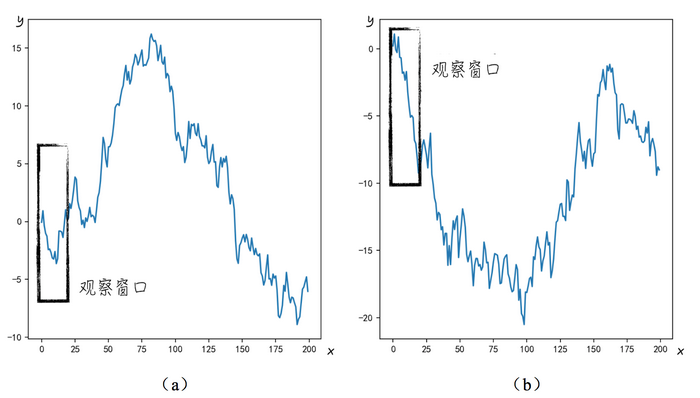
圖6上面的例子就是所謂的模型幻覺：表面上找到了數(shù)據(jù)變動的規(guī)律，但其實(shí)只是由隨機(jī)擾動引起的數(shù)字巧合。因此在對搭建模型時(shí)，必須時(shí)刻保持警惕，不然很容易掉進(jìn)數(shù)據(jù)的“陷阱”里，被數(shù)據(jù)給騙了，而這正是數(shù)據(jù)科學(xué)的研究重點(diǎn)。這門學(xué)科會“小心翼翼”地處理它的各種模型，以確保模型能擺脫數(shù)據(jù)中隨機(jī)因素的干擾，得到穩(wěn)定且正確的結(jié)論。