揭開數組的真面目
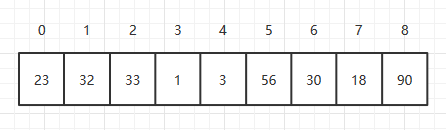
數組做為一種基礎的數據存儲結構,應用十分廣泛。數組是用連續的內存空間來存儲固定長度的、相同數據類型的一種數據結構。數據結構是跟語言無關的,這里,使用java來進行數組的相關操作。數組的索引是從0開始的。
一 數組初始化
創建數據有兩種方式,一種是先申請一個固定長度的數據,然后再給數組賦值,另一種是直接賦值。
第一種:
- 數據類型[] 數組名稱 = new 數據類型[長度];
這里的[]標識這申明了一個數組,這個[]除了可以放在數據類型后面,也可以放在數組名詞后面,效果一樣。假如我申明一個長度為2的long類型的數組,并賦值:
- long[] arr = new long[2];
- arr[0] = 1;
- arr[1] = 2;
第二種:
- 數據類型[] 數組名稱 = {元素1,元素2, ...};
這樣在數組初始化的時候直接給數組賦值,數組的長度由元素的個數決定。
二 自定義類封裝數組實現數據操作
- public class MyArray {
- // 自定義數組
- private long[] arr;
- // 有效數據長度
- private int element;
- public MyArray(){
- arr = new long[9];
- }
- public MyArray(int maxsize){
- arr = new long[maxsize];
- }
- /**
- * 顯示數組元素
- */
- public void display(){
- System.out.print("[");
- for (int i = 0; i < element; i++) {
- System.out.print(arr[i]+" ");
- }
- System.out.print("]");
- }
- }
2.1 添加元素
數組是用連續的內存空間來存儲數據的,則每次添加的時候會往當前數組的最后一個元素上添加元素,一次就可以加上元素,所以它的復雜度為O(1),假如定義一個長度為9數組,數組中已經有兩個元素,則添加第三個元素如下:
- public void add(long value){
- arr[element] = value;
- element++;
- }
2.2 根據值查詢元素位置
這種查找方式也叫做線性查找,就是根據傳入的值循環去遍歷元素,來獲取對應的位置,理論上平均查詢一個元素需要花費N/2次,所以它的復雜度為O(N)。
- public int find(long value){
- int i;
- for (i = 0; i < element; i++) {
- if(value == arr[i]){
- break;
- }
- }
- if(i == element){
- return -1;
- }else {
- return i;
- }
- }
2.3 根據索引查詢元素
根據索引來查找元素,也就是獲取對應位置的元素,其復雜度為O(1)。
- public long get(int index){
- if(index >= element || index < 0){
- throw new ArrayIndexOutOfBoundsException();
- }else {
- return arr[index];
- }
- }
2.4 根據索引刪除元素刪除對應索引的元素后,我們需要將所有改索引后面的元素,向前移動一位。假如我要刪除索引為2的元素,如下:
理論上平均刪除一個元素,我們需要移動N/2次,所以它的時間復雜度也為O(1)。
- public void delete(int index){
- if(index >= element || index < 0){
- throw new ArrayIndexOutOfBoundsException();
- }else {
- for (int i = index; i < element; i++) {
- arr[index] = arr[index+1];
- }
- element --;
- }
- }
2.5 修改元素
修改某個位置的元素,直接根據索引就一次就可以修改對應的元素,所以它的時間復雜度為O(1)。
- public void change(int index,long newValue){
- if(index >= element || index < 0){
- throw new ArrayIndexOutOfBoundsException();
- }else {
- arr[index] = newValue;
- }
- }
三 有序數組
有序數組是數組的一種特殊類型,有序數組中的元素按照某種順序進行排列。
3.1 添加元素
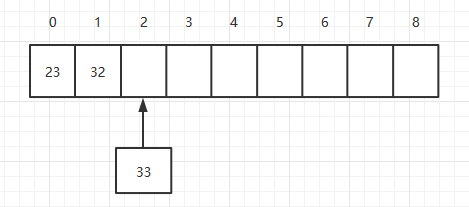
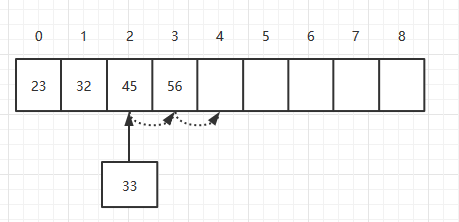
在添加元素的時候,將元素按順序添加到某個位置。如下,在一個數組中添加一個33的元素。
首先,將索引為3的元素移動到索引為4的位置,然后將索引為2的元素移動到索引為3的位置,最后將33添加到索引為2的位置。理論上插入一個元素需要移動元素的個數為N/2個,所以它的時間復雜度為O(N)。
- public void add(long value){
- int i;
- for (i = 0; i < element; i++) {
- if(arr[i]>value){
- break;
- }
- }
- for (int j = element; j > i; j--){
- arr[j] = arr[j-1];
- }
- arr[i] = value;
- element++;
- }
3.2 二分法根據元素查詢索引
在無序數組中,使用線性法進行查找相關元素,線性法即按索引按個查找。有序數組可以使用二分法來查找元素,二分法是指將一個數組從中間分成兩個,判斷元素位于哪個數組中,然后重復這樣的操作。
假如有8個元素的一個數組,數組內容為有序的0-7的序列,要查找5這個元素,第一次分成0-3和4-7兩個數組,然后再將4-7分成4-5和6-7兩個數組,最后再將4-5分成4和5就查詢出來具體的元素了,這樣分割3次就可以查詢出長度為8的數組中具體的元素,其復雜度即為O(logN)(logN在計算機中底數一般指的是2,意思為2的幾次方等于n)。
- public int search(long value){
- // 中間值
- int middle = 0;
- // 最小值
- int low = 0;
- // 最大值
- int pow = element;
- while (true){
- middle = (low + pow) / 2;
- if(arr[middle] == value){
- return middle;
- }else if (low > pow){
- return -1;
- }else{
- if(arr[middle] > value){
- pow = middle - 1;
- }else{
- low = middle + 1;
- }
- }
- }
- }
四 總結
復雜度越低意味著算法更加優秀,所以O(1) > O(logN) > O(N) > O(N^2)。
| 算法 | 復雜度 |
|---|---|
| 線性查找 | O(N) |
| 二分法查找 | O(logN) |
| 無序數組插入 | O(1) |
| 有序數組插入 | O(N) |
| 無序數組刪除 | O(N) |
| 有序數組刪除 | O(N) |
- 無序數組插入快,查找和刪除慢
- 有序數組查找快,插入和刪除慢
本文轉載自微信公眾號「Java旅途」,可以通過以下二維碼關注。轉載本文請聯系Java旅途公眾號。