6中常見的排序算法有GIF動(dòng)圖，更加容易幫助你理解其中的排序思想。

6種排序如下👇

冒泡排序
計(jì)數(shù)排序
快速排序
歸并排序
插入排序
選擇排序
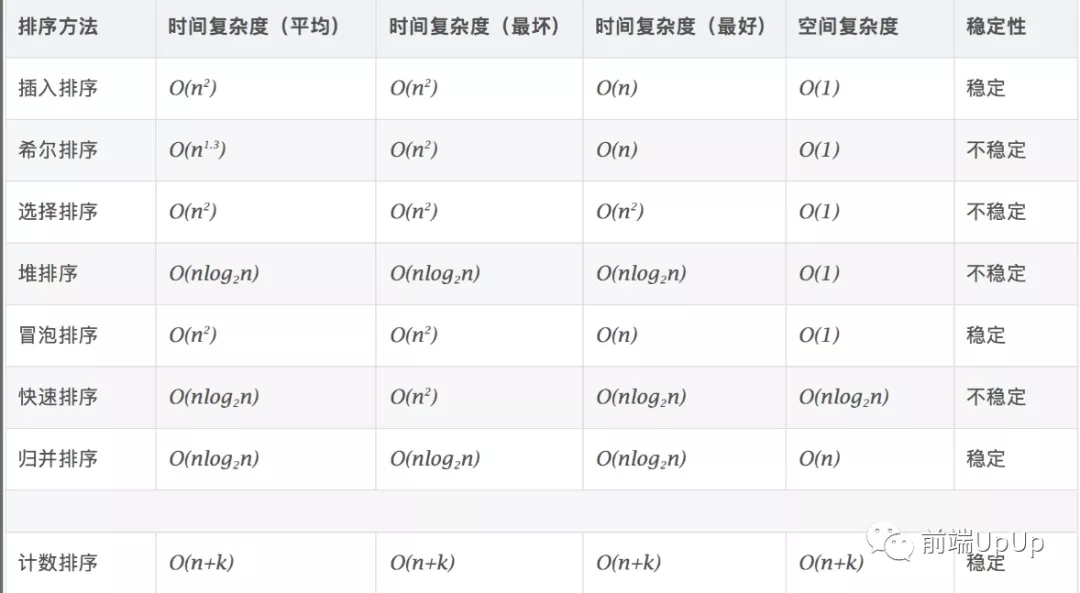
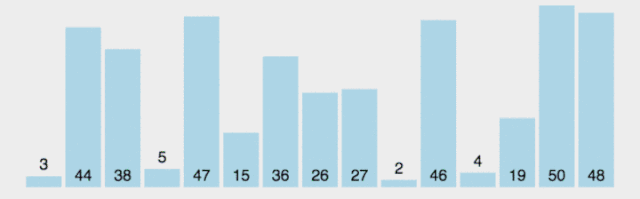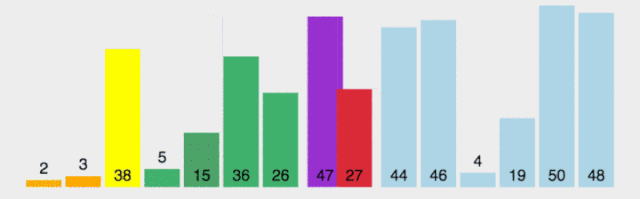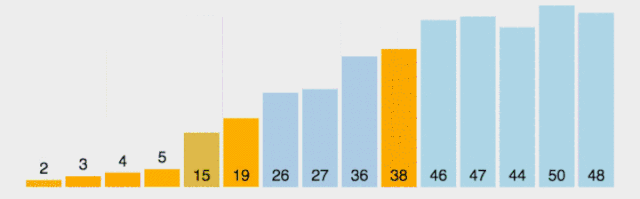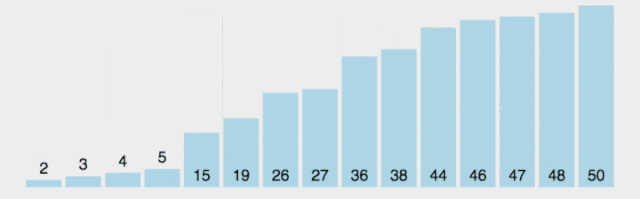
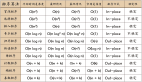
時(shí)間復(fù)雜度如下圖👇

排序算法復(fù)雜度分析
冒泡排序
以下動(dòng)圖GIF來自知乎 帥地

冒泡排序
這個(gè)名字的由來是向泡泡一樣浮起來，腦補(bǔ)一下，就是每次比較相鄰的兩個(gè)元素大小，然后慢慢'漂浮'起來，看思路吧。

「時(shí)間復(fù)雜度O(n*n)」

思路
1 比較相鄰的元素，前者比后者大的話，兩者交換位置。
2 對(duì)每一對(duì)相鄰元素做相同操作，從開始第一對(duì)到最后一對(duì)，這樣子最后的元素就是最大元素。
3 針對(duì)n個(gè)元素重復(fù)以上步驟，每次循環(huán)排除當(dāng)前最后一個(gè)。
4 重復(fù)步驟1~3，直到排序完成。

代碼實(shí)現(xiàn)

// 最外層循環(huán)控制的內(nèi)容是循環(huán)次數(shù) 
// 每一次比較的內(nèi)容都是相鄰兩者之間的大小關(guān)系 
let BubbleSort = function (arr, flag = 0) { 
    let len = arr.length 
 
    for (let i = 0; i < len - 1; i++) { 
        for (let j = 0; j < len - 1 - i; j++) { 
            if (arr[j] > arr[j + 1]) { 
                [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]] 
            } 
        } 
    } 
    return flag ? arr.reverse() : arr 
} 
 
let arr = [2, 9, 6, 7, 4, 3, 1, 7] 
console.log(BubbleSort(arr, 1)) 

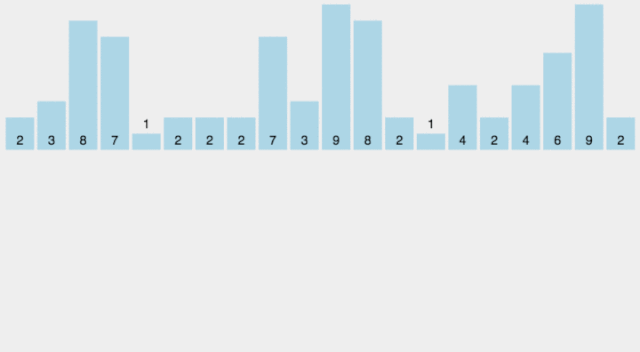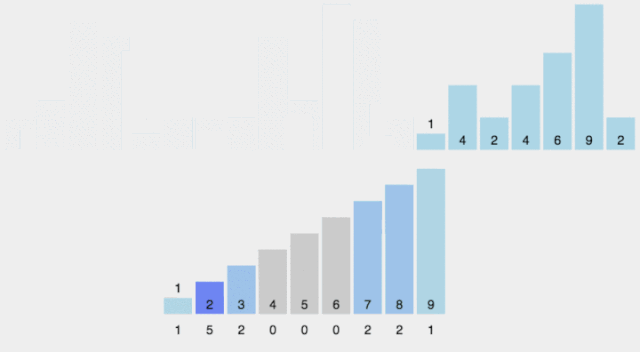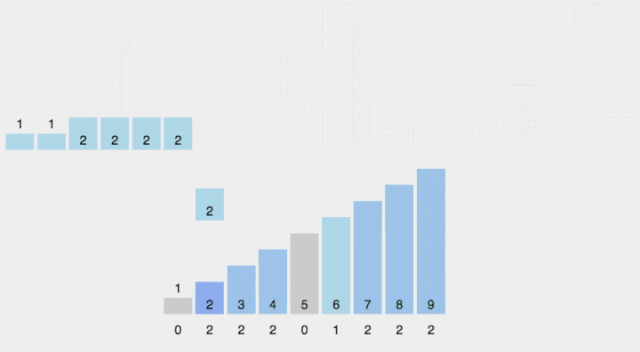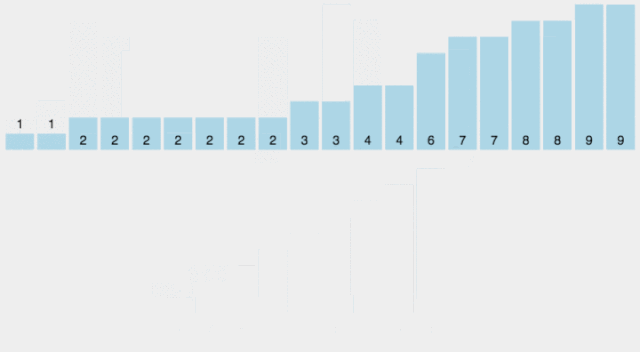
計(jì)數(shù)排序
從名稱上就知道，它的思想：就是把數(shù)組元素作為數(shù)組的下標(biāo)，然后用一個(gè)臨時(shí)數(shù)組統(tǒng)計(jì)該元素出現(xiàn)的次數(shù)。

數(shù)組的數(shù)據(jù)必須是整數(shù)，而且最大最小值相差的值不要過大，對(duì)于「數(shù)據(jù)是負(fù)數(shù)的話，我實(shí)現(xiàn)的方案對(duì)此有優(yōu)化」。

「時(shí)間復(fù)雜度：O(n+k)」

思路
1.計(jì)算出差值d,最小值小于0,加上本身add

2.創(chuàng)建統(tǒng)計(jì)數(shù)組并統(tǒng)計(jì)對(duì)應(yīng)元素個(gè)數(shù)

3.統(tǒng)計(jì)數(shù)組做變形，后面的元素等于前面的元素之和,也就是排名數(shù)組

4.遍歷原始數(shù)組,從統(tǒng)計(jì)數(shù)組中找到正確位置,輸出到結(jié)果數(shù)組

動(dòng)畫

計(jì)數(shù)排序
代碼實(shí)現(xiàn)

// 計(jì)數(shù)排序 
let countingSort = function(arr, flag = 0) { 
    let min = arr[0], 
        max = arr[0], 
        len = arr.length; 
    // 求最大最小值 
    for(let i = 0; i < len; i++) { 
        max = Math.max(arr[i], max) 
        min = Math.min(arr[i], min) 
    } 
    // 1.計(jì)算出差值d,最小值小于0,加上本身add 
 
    let d =  max - min, 
        add = min < 0 ? -min : 0; 
    //2.創(chuàng)建統(tǒng)計(jì)數(shù)組并統(tǒng)計(jì)對(duì)應(yīng)元素個(gè)數(shù)     
    let countArray  = new Array(d+1+add).fill(0) 
    for(let i = 0; i < len; i++){ 
        let demp = arr[i]- min + add 
        countArray[ demp ] += 1  
    } 
     
    //3.統(tǒng)計(jì)數(shù)組做變形，后面的元素等于前面的元素之和,也就是排名數(shù)組 
    let sum = 0; 
 
    // 這里需要遍歷的是countArray數(shù)組長(zhǎng)度 
    for(let i = 0; i < d+1+add; i++){ 
        sum += countArray[i] 
        countArray[i] = sum; 
    } 
    let res = new Array(len) 
    //4.遍歷原始數(shù)組,從統(tǒng)計(jì)數(shù)組中找到正確位置,輸出到結(jié)果數(shù)組 
    for(let i = 0; i < len; i++){ 
        let demp = arr[i] -min + add 
        res[ countArray[demp] -1 ] = arr[i] 
        countArray[demp] --; 
    } 
    return flag ? res.reverse() : res 
} 
 
let arr = [2, 9, 6, 7, 4, 3, 1, 7,0,-1,-2] 
console.log(countingSort(arr)) 

快速排序
基本思想：通過一趟排序?qū)⒋庞涗浄指舫瑟?dú)立的兩部分，其中一部分記錄的關(guān)鍵字均比另一部分的關(guān)鍵字小，則可分別對(duì)這兩部分記錄繼續(xù)進(jìn)行排序，以達(dá)到整個(gè)序列有序。

「時(shí)間復(fù)雜度：O(nlogn)」

思路
選擇數(shù)組中間數(shù)作為基數(shù)，并從數(shù)組中取出此基數(shù)
準(zhǔn)備兩個(gè)數(shù)組容器，遍歷數(shù)組，逐個(gè)與基數(shù)比對(duì)，較小的放左邊容器，較大的放右邊容器；
遞歸處理兩個(gè)容器的元素，并將處理后的數(shù)據(jù)與基數(shù)按大小合并成一個(gè)數(shù)組，返回。
動(dòng)畫

快速排序

let quickSort = function (arr) { 
    // 遞歸出口就是數(shù)組長(zhǎng)度為1 
    if (arr.length <= 1) return arr 
    //獲取中間值的索引，使用Math.floor向下取整； 
    let index = Math.floor(arr.length / 2) 
    // 使用splice截取中間值，第一個(gè)參數(shù)為截取的索引，第二個(gè)參數(shù)為截取的長(zhǎng)度； 
    // 如果此處使用pivot=arr[index]; 那么將會(huì)出現(xiàn)無限遞歸的錯(cuò)誤； 
    // splice影響原數(shù)組 
    let pivot = arr.splice(index, 1)[0], 
        left = [], 
        right = []; 
    console.log(pivot) 
    console.log(arr) 
    for (let i = 0; i < arr.length; i++) { 
        if (pivot > arr[i]) { 
            left.push(arr[i]) 
        } else { 
            right.push(arr[i]) 
        } 
    } 
    return quickSort(left).concat([pivot], quickSort(right)); 
} 
 
//let arr = [2, 9, 6, 7, 4, 3, 1, 7] 
// console.log(quickSort(arr)) 

歸并排序

將兩個(gè)有序數(shù)列合并成一個(gè)有序數(shù)列，我們稱之為“歸并”

基本思想與過程：先遞歸的分解數(shù)列，再合并數(shù)列（分治思想的典型應(yīng)用）

「時(shí)間復(fù)雜度: O(nlog(n))」

思路
將一個(gè)數(shù)組拆成A、B兩個(gè)小組，兩個(gè)小組繼續(xù)拆，直到每個(gè)小組只有一個(gè)元素為止。
按照拆分過程逐步合并小組，由于各小組初始只有一個(gè)元素，可以看做小組內(nèi)部是有序的，合并小組可以被看做是合并兩個(gè)有序數(shù)組的過程。
對(duì)左右兩個(gè)小數(shù)列重復(fù)第二步，直至各區(qū)間只有1個(gè)數(shù)。
動(dòng)畫

歸并排序
代碼實(shí)現(xiàn)

const merge = (left, right) => { // 合并數(shù)組 
 
    let result = [] 
    // 使用shift()方法偷個(gè)懶,刪除第一個(gè)元素,并且返回該值 
    while (left.length && right.length) { 
        if (left[0] <= right[0]) { 
            result.push(left.shift()) 
        } else { 
            result.push(right.shift()) 
        } 
    } 
    while (left.length) { 
        result.push(left.shift()) 
    } 
 
    while (right.length) { 
        result.push(right.shift()) 
    } 
    return result 
} 
 
let mergeSort = function (arr) { 
    if (arr.length <= 1) 
        return arr 
    let mid = Math.floor(arr.length / 2) 
    // 拆分?jǐn)?shù)組 
    let left = arr.slice(0, mid), 
        right = arr.slice(mid); 
    let mergeLeftArray = mergeSort(left), 
        mergeRightArray = mergeSort(right) 
    return merge(mergeLeftArray, mergeRightArray) 
} 
 
let arr = [2, 9, 6, 7, 4, 3, 1, 7, 0, -1, -2] 
console.log(mergeSort(arr)) 

插入排序
顧名思義：通過構(gòu)建有序序列，對(duì)于未排序數(shù)據(jù)，在已排序序列中從后向前掃描，找到相應(yīng)位置并插入。

「時(shí)間復(fù)雜度: O(n*n)」

思路
從第一個(gè)元素開始，該元素可以認(rèn)為已經(jīng)被排序；
取出下一個(gè)元素，在已經(jīng)排序的元素序列中從后向前掃描；
如果該元素（已排序）大于新元素，將該元素移到下一位置；
重復(fù)步驟3，直到找到已排序的元素小于或者等于新元素的位置；
重復(fù)步驟2~5。

代碼實(shí)現(xiàn)

let insertionSort = function (arr) { 
    let len = arr.length 
 
    for (let i = 0; i < len; i++) { 
        let preIndex = i - 1, 
            cur = arr[i]; 
        while (preIndex >= 0 && arr[preIndex] > cur) { 
            arr[preIndex + 1] = arr[preIndex] 
            preIndex--; 
        } 
        arr[preIndex + 1] = cur 
    } 
    return arr 
} 
 
 
let arr = [2, 9, 6, 7, 4, 3, 1, 7, 0, -1, -2] 
console.log(insertionSort(arr)) 

選擇排序
思路：每一次從待排序的數(shù)組元素中選擇最大(最小)的一個(gè)元素作為首元素,直到排完為止

「時(shí)間復(fù)雜度O(n*n)」

思路
1.有n個(gè)數(shù),需要排序n-1次
2.第一次選擇最小值,放在第一位
3.第二次選擇最小值,放在第二位
4.…..重復(fù)該過程
5.第n-1次選擇最小值,放在第n-1位
代碼實(shí)現(xiàn)

let selectSort = function (arr, flag = 0) { 
    let len = arr.length, 
        temp = 0; 
 
    // 一共需要排序len-1次 
    for (let i = 0; i < len - 1; i++) { 
        temp = i; 
        for (let j = i + 1; j < len; j++) { 
            if (arr[j] < arr[temp]) 
                temp = j; 
        } 
        // 每一趟保證第i位為最小值 
        if (temp !== i) { 
            [arr[i], arr[temp]] = [arr[temp], arr[i]] 
        } 
    } 
 
    return flag ? arr.reverse() : arr 
} 
 
 
 
let arr = [2, 9, 6, 7, 4, 3, 1, 7, 0, -1, -2] 
console.log(selectSort(arr, 1))