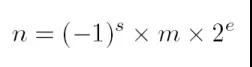[[345691]]

 

 

 

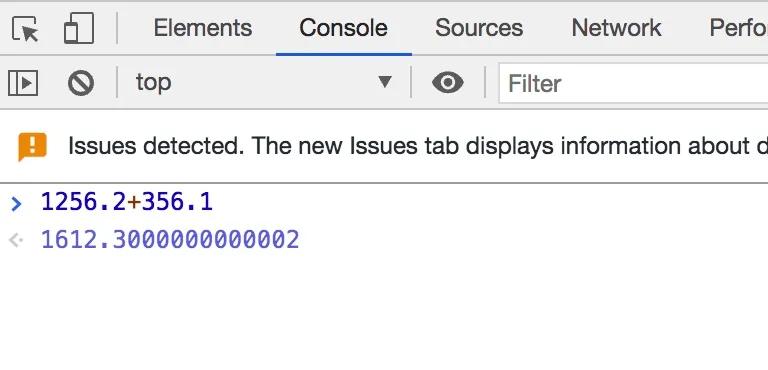
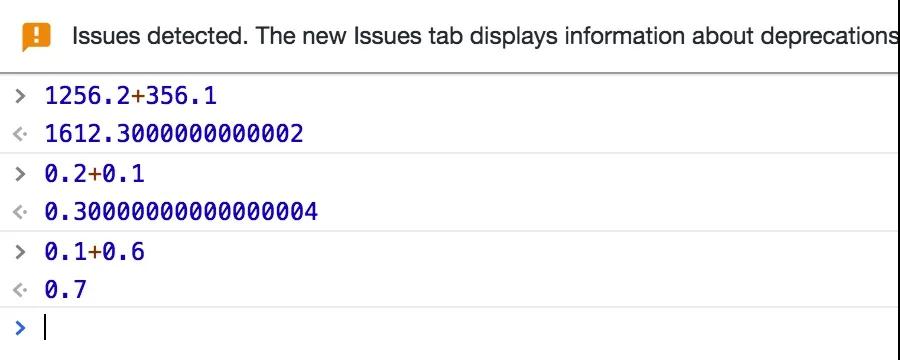
為什么當我們使用電腦瀏覽器計算0.2+0.1的時候，解決卻是0.30000000000000004，而0.1+0.6的結果卻是0.7呢?

這個問題其實一直是一個經典的問題，甚至有一個網站的域名就是https://0.30000000000000004.com/ ，主要就是解釋這個問題的。

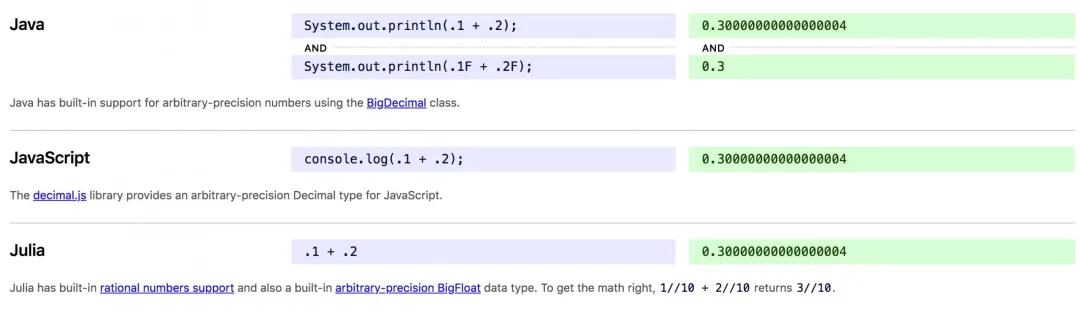
在這個網站中，列舉了各種編程語言中計算0.2+0.1的結果，摘選幾個如下：

 

 

 

 

可以看到，在各種語言中，計算0.2+0.1的結果都出奇的一致，那就是這個神奇的0.30000000000000004。

其實，當我們使用瀏覽器的控制臺(F12)進行計算的時候，用到的就是JavaScript語言進行計算的，所以，前面的現象，歸根結底其實和具體的編程語言無關。

主要問題還是計算機中到底是如何表示小數以及如何進行小數運算的。

 

我們知道，計算機只認識0和1 [為什么計算機只認識0和1]，現實世界中的內容想要通過計算機存儲、計算或者展示，都需要轉換2進制。在現實世界中，數字主要有整數和小數兩種。

在之前的[為什么計算機用補碼存儲數據]這篇文章中，我們介紹過，計算機中表示整數的方式有很多，如原碼、反碼以及補碼等。

整數包括正整數、負整數以及零。在計算機中存儲的整數則分為有符號數和無符號數。

對于無符號數，采用哪種編碼方式都無所謂，對于有符號數的編碼方式，常用的是補碼。

那么，一個十進制數字想要獲得其二進制的補碼，需要先通過一定的算法得到他對應的原碼。

 

十進制轉二進制

首先我們看一下，如何把十進制整數轉換成二進制整數?

十進制整數轉換為二進制整數采用"除2取余，逆序排列"法。

具體做法是：

用2整除十進制整數，可以得到一個商和余數;

再用2去除商，又會得到一個商和余數，如此進行，直到商為小于1時為止

然后把先得到的余數作為二進制數的低位有效位，后得到的余數作為二進制數的高位有效位，依次排列起來。

如，我們想要把127轉換成二進制，做法如下：

 

 

 

那么，十進制小數轉換成二進制小數，又該如何計算呢?

十進制小數轉換成二進制小數采用"乘2取整，順序排列"法。

具體做法是：* 用2乘十進制小數，可以得到積 * 將積的整數部分取出，再用2乘余下的小數部分，又得到一個積 * 再將積的整數部分取出，如此進行，直到積中的小數部分為零，此時0或1為二進制的最后一位。或者達到所要求的精度為止。

 

所以，十進制的0.625對應的二進制就是0.101。

 

不是所有數都能用二進制表示

我們知道了如何將一個十進制小數轉換成二進制，那么是不是計算就可以直接用二進制表示小數了呢?

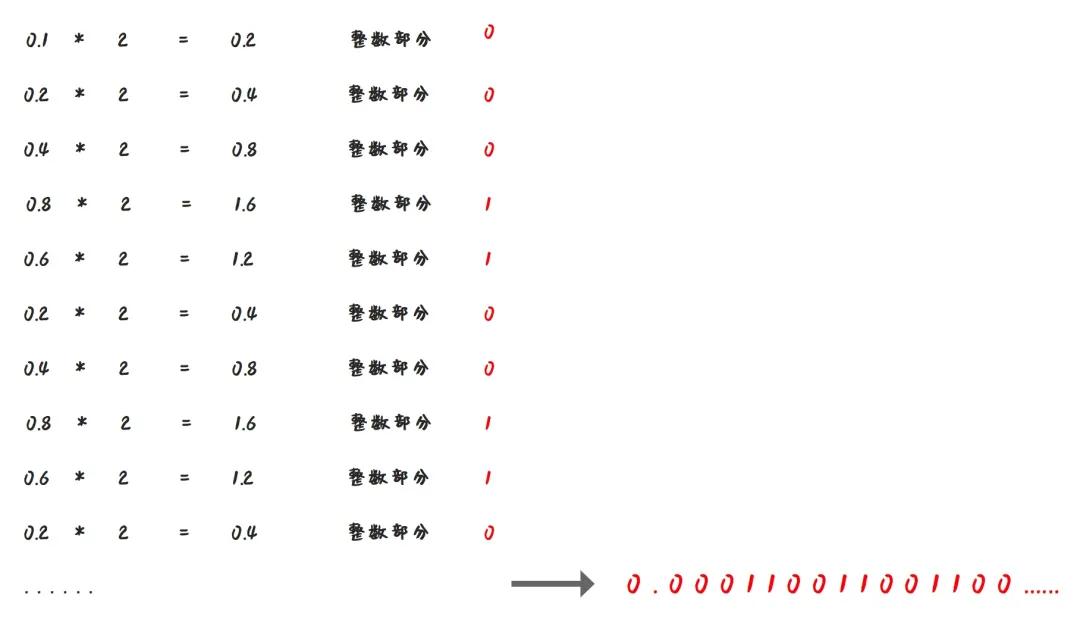
前面我們的例子中0.625是一個特列，那么還是用同樣的算法，請計算下0.1對應的二進制是多少?

 

我們發現，0.1的二進制表示中出現了無限循環的情況，也就是(0.1)10 = (0.000110011001100…)2

這種情況，計算機就沒辦法用二進制精確的表示0.1了。

也就是說，對于像0.1這種數字，我們是沒辦法將他轉換成一個確定的二進制數的。

 

IEEE 754

為了解決部分小數無法使用二進制精確表示的問題，于是就有了IEEE 754規范。

IEEE二進制浮點數算術標準(IEEE 754)是20世紀80年代以來最廣泛使用的浮點數運算標準，為許多CPU與浮點運算器所采用。

浮點數和小數并不是完全一樣的，計算機中小數的表示法，其實有定點和浮點兩種。因為在位數相同的情況下，定點數的表示范圍要比浮點數小。所以在計算機科學中，使用浮點數來表示實數的近似值。

IEEE 754規定了四種表示浮點數值的方式：單精確度(32位)、雙精確度(64位)、延伸單精確度(43比特以上，很少使用)與延伸雙精確度(79比特以上，通常以80位實現)。

其中最常用的就是32位單精度浮點數和64位雙精度浮點數。

IEEE并沒有解決小數無法精確表示的問題，只是提出了一種使用近似值表示小數的方式，并且引入了精度的概念。

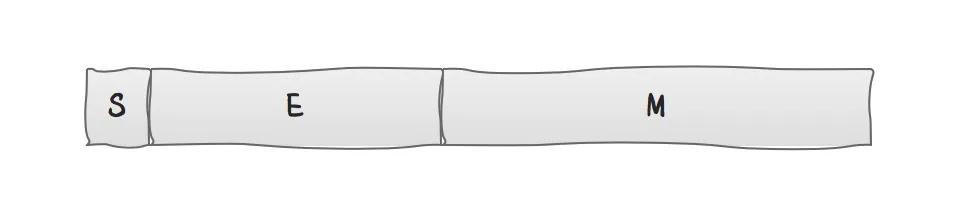
浮點數是一串0和1構成的位序列(bit sequence)，從邏輯上用三元組{S,E,M}表示一個數N,如下圖所示：

 

S(sign)表示N的符號位。對應值s滿足：n>0時，s=0; n≤0時，s=1。

E(exponent)表示N的指數位，位于S和M之間的若干位。對應值e值也可正可負。

M(mantissa)表示N的尾數位，恰好，它位于N末尾。M也叫有效數字位(significand)、系數位(coefficient), 甚至被稱作"小數"。

則浮點數N的實際值n由下方的式子表示：

 

上面這個公式看起來很復雜，其中符號位和尾數位還比較容易理解，但是這個指數位就不是那么容易理解了。

其實，大家也不用太過于糾結這個公式，大家只需要知道對于單精度浮點數，最多只能用32位字符表示一個數字，雙精度浮點數最多只能用64位來表示一個數字。

而對于那些無限循環的二進制數來說，計算機采用浮點數的方式保留了一定的有效數字，那么這個值只能是近似值，不可能是真實值。

至于一個數對應的IEEE 754浮點數應該如何計算，不是本文的重點，這里就不再贅述了，過程還是比較復雜的，需要進行對階、尾數求和、規格化、舍入以及溢出判斷等。

但是這些其實不需要了解的太詳細，我們只需要知道，小數在計算機中的表示是近似數，并不是真實值。根據精度不同，近似程度也有所不同。

如0.1這個小數，他對應的在雙精度浮點數的二進制為：0.00011001100110011001100110011001100110011001100110011001 。

0.2這個小數0.00110011001100110011001100110011001100110011001100110011 。

所以兩者相加：

 

轉換成10進制之后得到：0.30000000000000004!

 

避免精度丟失

在Java中，使用float表示單精度浮點數，double表示雙精度浮點數，表示的都是近似值。

所以，在Java代碼中，千萬不要使用float或者double來進行高精度運算，尤其是金額運算，否則就很容易產生資損問題。

為了解決這樣的精度問題，Java中提供了BigDecimal來進行精確運算。

 

參考資料：

https://0.30000000000000004.com/

https://zh.wikipedia.org/zh-hans/IEEE_754

https://www.h-schmidt.net/FloatConverter/IEEE754.html

關于作者：漫話編程，是一個通過漫畫+音頻的形式講解枯燥的編程知識的公眾號。致力于讓編程變得更有樂趣。

本文轉載自微信公眾號「漫話編程」，可以通過以下二維碼關注。轉載本文請聯系漫話編程公眾號。