本文經(jīng)AI新媒體量子位（公眾號ID:QbitAI）授權轉載，轉載請聯(lián)系出處。

數(shù)學和計算機的關系，一直是你中有我、我中有你。

計算機程序離不開數(shù)學，同時也給數(shù)學計算帶來便利。

國外知名科普網(wǎng)站Quanta Magazine，對2020年計算機、數(shù)學這兩門學科的幾項重大突破，進行了盤點。

這里面，有困擾了數(shù)學家50余年的謎題破解，也有AI與數(shù)學結合的身影。

當然，兩名數(shù)學家疫情隔離期間，破解陶哲軒挑戰(zhàn)失敗的百年數(shù)學問題，也榜上有名。

一起來看看。

TOP1：“量子糾纏”重大突破

今年，計算機領域最重要的突破，是MIP*=RE的證明。

它的證明，意味著利用量子邏輯來計算的量子計算機（而非利用0和1進行計算的經(jīng)典計算機），可以從理論上驗證大量問題的答案。

來自悉尼科技大學、加州理工學院、德克薩斯大學奧斯汀分校、和多倫多大學的五位計算機科學家，將研究成果聯(lián)名發(fā)表在了一篇叫做《MIP * = RE》的論文上。

這篇論文證明，由經(jīng)典驗證與多個量子理論驗證相互作用而確定的語言類別MIP，等同于遞歸可枚舉語言類RE。

也就是說，MIP*=RE多方交互式證明、加上量子糾纏的計算能力，給圖靈停機問題提供了一個思路。

對于這篇論文的結論，物理學家在里面看到Tsirelson的物理問題的答案，數(shù)學家在里面得到了Connes嵌入猜想的答案。

作者之一的Henry Yuen說道：“如同盲人摸象一樣，不同科學領域的人，領略到不同部分，雖然都是正確的，但是都還沒搞清楚大象的原貌。”

80年代，計算機科學家發(fā)明了交互證明理論和概率可驗證明(PCP)，MIP* = RE則是經(jīng)典的PCP定理，能夠在量子糾纏的幫助下遞歸到無窮。

論文得出結論說，兩臺機器相互糾纏、相互驗證，可以用于解決圖靈停機問題。同時，還證明了Connes嵌入猜想是錯誤的。

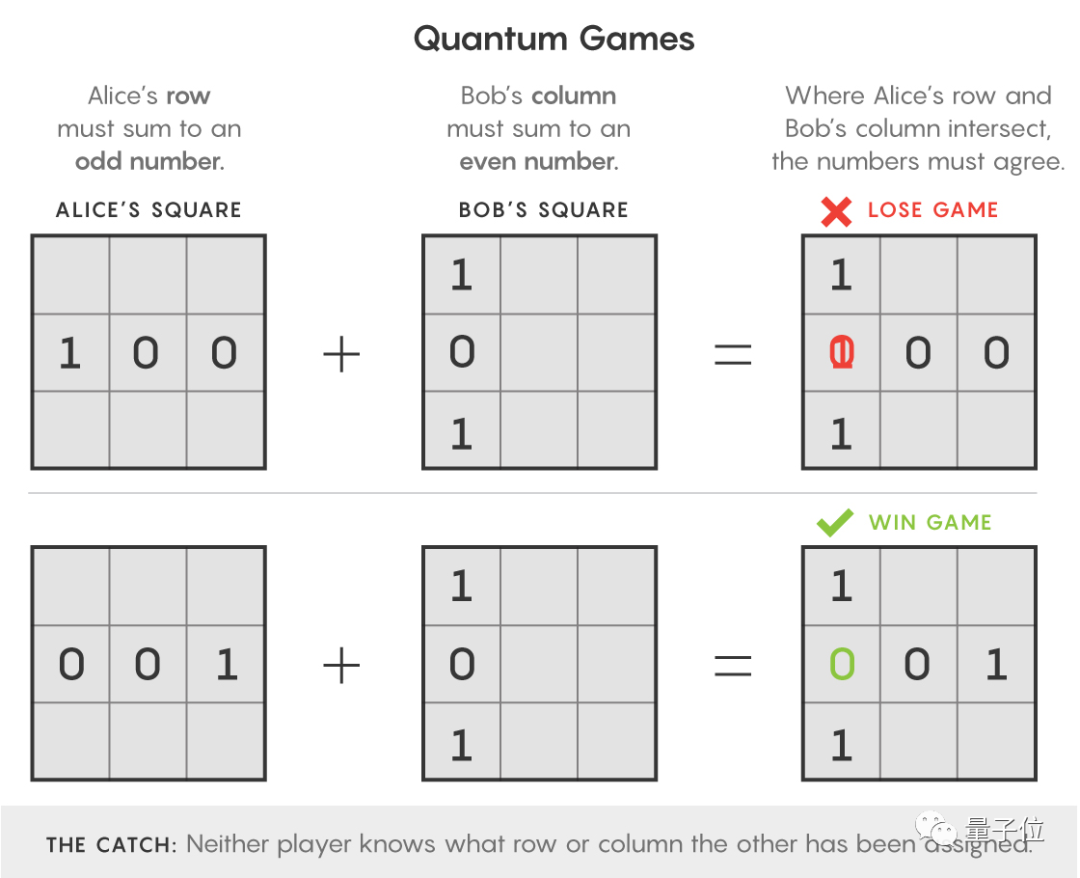
他們還引用了經(jīng)典的兩個博弈互證游戲Bell / CHSH，兩者無窮無盡的糾纏驗證，會提高游戲的勝率。所以最終問題，還是怎么讓這個糾纏驗證的過程停止的問題。

此外，這篇論文的一作，是悉尼科技大學量子軟件與信息中心季錚鋒教授。

季錚鋒曾于2007年，獲得清華大學計算機科學與技術的博士學位。

論文地址：
https://arxiv.org/abs/2001.04383

TOP2：破解“康威扭結”

今年6月，英國著名數(shù)學家約翰·康威（John Conway）因患新冠肺炎逝世，留下一個困擾數(shù)學界50年的難題“康威扭結”（Conway Knot）。

在他逝世一個月之后，德州大學奧斯汀分校的一位博士小姐姐Lisa Piccirillo，花了一周的時間將其解決了。

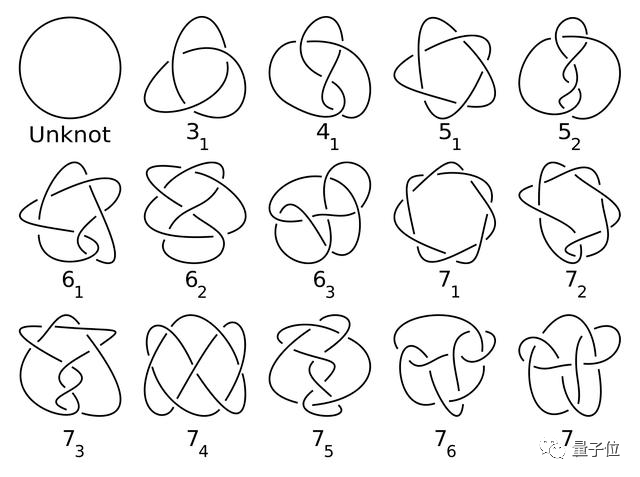
多年來，數(shù)學家們發(fā)現(xiàn)了形形色色的扭結，這些結在拓撲學上可切，但并不是平滑可切。然而，這些扭結的交叉都大于12。

而在交叉點數(shù)小于12的扭結中，只有康威結的切片狀態(tài)一直無法找到。

康威扭結是否平滑可切為何如此重要？

因為平滑可切的扭結，為數(shù)學家提供了一條探索四維空間奇特屬性的途徑。

所以，康威扭結是否為平滑可切，成為了扭結理論重大突破的硬性標準。

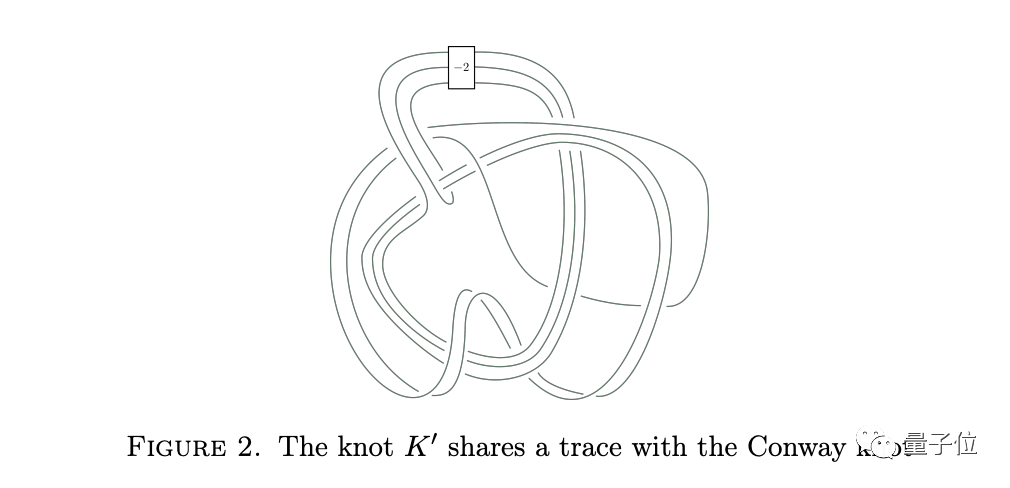
Lisa認為，如果可以為康威扭結構造一個相同跡的扭結，那么也許可以更好地與可切不變性配合使用。

于是，她設法構造了一個復雜的扭結，它的跡與康威扭結相同。Lisa使用了一種叫做拉斯穆森S不變量（Rasmussen’s s-invariant）的工具。

結果顯示她構造出來的扭結不是平滑可切的，因此推斷出，康威扭結也不是平滑可切的。

“這是一個非常美麗的證明。”數(shù)學家們紛紛贊嘆說。

閱讀延伸：
https://mp.weixin.qq.com/s/4wGmSxKGFVEqW_wdWWVtog

TOP3：參加IMO的AI

數(shù)學已經(jīng)有了數(shù)千年的發(fā)展歷史，而人類的記憶力有限，即使是一流的數(shù)學家，也記不住全部的數(shù)學公式和定理。

于是很多數(shù)學科學家轉向了“數(shù)學數(shù)字化”，將數(shù)千年累積的數(shù)學成果，建成一個數(shù)字圖書館。

在微軟的一個名為Lean的軟件程序上，數(shù)學家們建立了一個叫做Mathlib的數(shù)學基礎數(shù)據(jù)庫，這個數(shù)據(jù)庫錄入了數(shù)學專業(yè)大二學生應學到的所有知識。

他們將數(shù)學知識匯編成計算機語言，在龐大的數(shù)學公式定理庫基礎上，解決數(shù)學難題。

Lean做題的方法跟象棋、圍棋AI的算法相同，都是遵循決策樹，直到算法找到最優(yōu)解。

目前，Lean正在籌劃參加下一屆的IMO（國際奧數(shù)競賽），比賽結果尚未可知，也有不少人持悲觀結果態(tài)度。

但是AI做復雜的數(shù)學題，是有特別成功案例的。

來自斯坦福大學、卡內基梅隆大學、羅徹斯特理工學院的幾位計算機研究者，通過AI的方式，僅用40臺電腦、30分鐘就解決了困擾數(shù)學家90年之久的凱勒猜想。

閱讀延伸：
https://mp.weixin.qq.com/s/bDD6-KAwLWPFAdV8khfIRw

那么，這一年在數(shù)學和計算領域還有什么新的突破呢？

幾何學進展

內接方形問題

疫情期間，兩位被封閉在家的科學家Andrew Lobb和Joshua Greene覺得百無聊賴。

于是他們動了動手指，解決了一個困擾百年的數(shù)學問題，這個數(shù)學難題，連陶哲軒都挑戰(zhàn)失敗了。

這個問題是：任何簡單閉合環(huán)路，是否總能在其上找到四個點形成一個任意長寬比矩形？

這個問題也叫做內接方形問題，源自1911年。德國數(shù)學家Otto Toeplitz預測稱，任何簡單閉合曲線，都包含四個可以連接形成正方形的點。

這句話聽起來很簡單，但從古至今，多少數(shù)學家費盡腦汁都沒有證明出來。

1977年，數(shù)學家Herbert Vaughan使用莫比烏斯帶解這個內接矩形問題，取得了突破性的進展。

他證明，在三維空間的任何閉合環(huán)路中，都至少存在這樣四個點，能夠構成一個矩形。

天才數(shù)學家陶哲軒，使用積分方法，解決了特定情況下的內接方形問題。

他用積分方法證明，在曲線由兩個常數(shù)小于 1 的 Lipschitz 圖形組成的這種特殊情況下，該曲線一定存在四個能組成正方形的點。

但是兩者都未證明：是否任意長寬比的矩形（包括正方形）都能存在。

在Andrew Lobb和Joshua Greene的方法中，他們將莫比烏斯帶嵌入四維辛空間中，證明了莫比烏斯帶可以嵌入到四維辛空間中而不相交。

這意味著每一個封閉的光滑曲線必須包含四個點的集合，這四個點可以連接在一起形成所有長寬比的矩形。

延伸閱讀：
https://mp.weixin.qq.com/s/E-I_3C-3m0KTI1XjYaKWcA

十二面體的新發(fā)現(xiàn)

數(shù)學家花了2000多年的時間，來研究正四、六、八、十二、二十面體，這些特殊形狀也叫做柏拉圖多面體。多年來，數(shù)學家仍對對它們知之甚少。

關于柏拉圖多面體一直有個思考，假設從柏拉圖立體的一個角出發(fā)，是否存在一條直線路徑，不用經(jīng)過其他角，就可以回到原來的角？

對于等邊三角形或者正方形組成的四面體、立方體、八面體、二十面體，科學家得出的具體結論是：不存在。必須經(jīng)過其他角，否則永遠回不到出發(fā)點。

然而正十二面體是由五邊形組成，是否也符合這個定理？

Jayadev Athreya，David Aulicino和Patrick Hooper在《實驗數(shù)學》雜志上發(fā)表了關于十二面體的研究。

他們認為，由于正十二面體由五邊形組成，五邊形和正十二面體又有幾何上的聯(lián)系，前者的高度對稱性可以用于闡明后者的結構。

因此，研究者能夠識別十二面體回到出發(fā)點所有直線路徑，并根據(jù)十二面體的隱藏對稱性對這些路徑進行分類。

正十二面體存在無數(shù)條這樣的直線路徑，這些路徑還可以劃分為31個自然族。

論文地址：
https://www.tandfonline.com/doi/abs/10.1080/10586458.2020.1712564

數(shù)學思想的升華

升級Langlands數(shù)學橋

17世紀法國數(shù)學家提出了“費馬最后的定理”。斷言，當整數(shù)n>2時，關于x，y，z的方程x2+y2=z2沒有正整數(shù)解。

1995年，它被英國數(shù)學家安德魯·威爾斯（Andrew Wiles）證明，經(jīng)歷了300多年。

威爾斯同時提出了數(shù)學橋的概念。意思是，這個等式就是兩個數(shù)學領域之間的橋梁，連接好這座橋，就解開了這個不定式。

然而這只是Langlands項目的一小部分。Langlands項目由加拿大數(shù)學家羅伯特·蘭蘭茲（Robert Langlands）提出，旨在研究數(shù)論與幾何之間聯(lián)系的網(wǎng)絡猜想，被看作是現(xiàn)代數(shù)學研究的最大項目。

△加拿大數(shù)學家Robert Langlands

數(shù)學家們將這個方法擴展到有理數(shù)系數(shù)和橢圓曲線之間的聯(lián)系。最近，還覆蓋到了簡單的無理數(shù)系數(shù)。但是涉及到了虛數(shù)，或者更高的指數(shù)，例如4或5，他們方法也不奏效了。

于是，芝加哥大學的Frank Calegari和Facebook的科學家David Geraghty為了克服上述障礙，在網(wǎng)上發(fā)布論文，是關于怎么建立一個更加通用的不定式的橋梁，并提出了三個猜想。

為了證實這三個猜想，數(shù)學家們迅速舉辦了一個秘密的研討會，整理成了有10個人署名的論文。

雖然這篇論文的研究成果在數(shù)學領域的Langlands項目中取得了巨大的突破，但是對于指數(shù)大于6，或者2個變量以上的不定式，仍舊沒有解決辦法。

所以，Langlands項目還有拓展空間。

數(shù)學論文地址：
https://arxiv.org/abs/1812.09999

多項式與冪級數(shù)

物理學中的排斥力，在數(shù)學中也存在。

多倫多大學的 Vesselin Dimitrov，就證明了它們的存在，并且獲得了實驗結果。

一般情況下，多項式的根數(shù)與其次數(shù)值一樣多。所以X2 - 4具有兩個根，而X 5 - 7 X 3 + 2 X 2 - 4 X - 9有五個根。

數(shù)學家很想知道多項式的根與根之間有什么聯(lián)系。

這里引入一個分圓多項式，所謂的分圓多項式就是不可約的多項式，數(shù)學家發(fā)現(xiàn)其根遵循特定的幾何方式，根都分布在一個圓內，取名叫做“團結之根”。

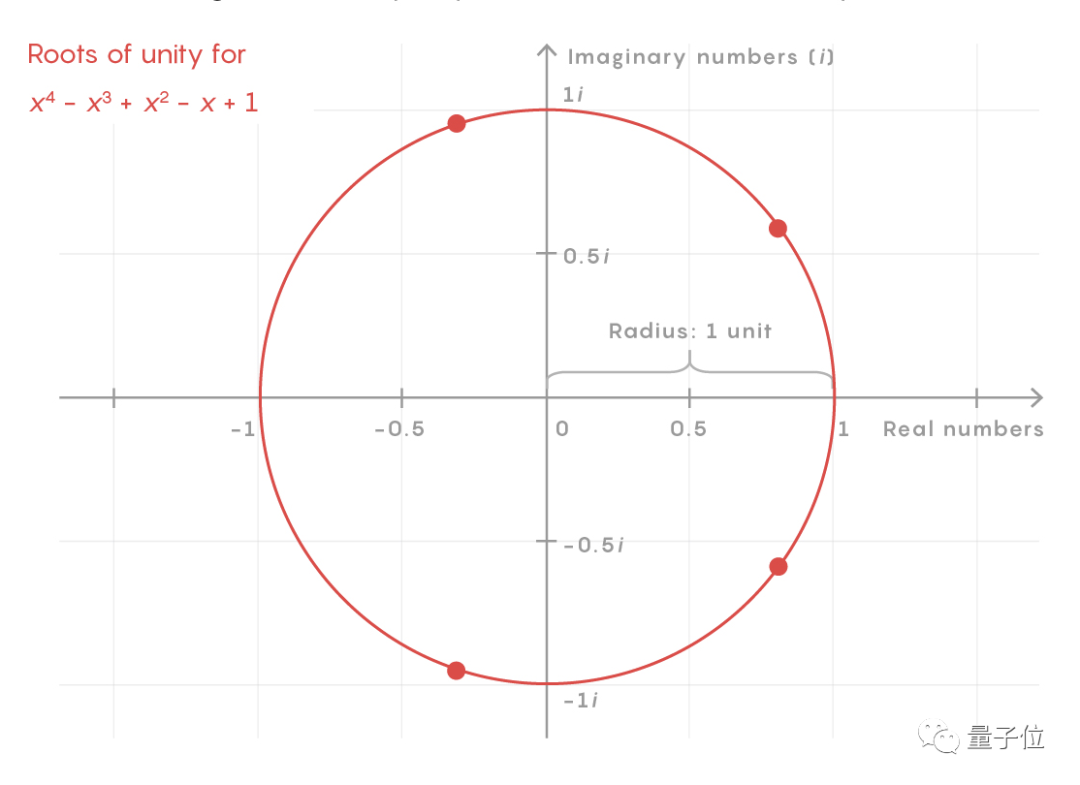
但是實際上，大多數(shù)都是非分圓多項式。

數(shù)學家預測，每個非分圓多項式必定有一個根在圓外。

他們猜想這個是由于“排斥力”，就像物理中的電子一樣，它們最小的根落在圓內，像磁鐵一樣擁有排斥力，將其他根排斥到圓外。

但是長期以來，數(shù)學家們沒能證明這個理論。

Dimitrov做到了，他將多項式的根的大小的問題轉換成冪級數(shù)。冪級數(shù)就像多項式，有無限個解。

他從一個非分圓多項式入手，找到它的根，并把這些根取不同的冪，再將它們相乘，然后取這個積的平方根。最后，根據(jù)這個平方根，構建出一個具有多項式本質屬性的冪級數(shù)。

Dimitrov證明了冪級數(shù)的系數(shù)必然是整數(shù)，如果它的Hankel determinants也很大，那么，非分圓多項式的一個初始根必然也很大。于是，就證明了多項式的根與冪級數(shù)之間的聯(lián)系。

其他數(shù)學家評論說：“他的方法很精妙，間接證明了關于排斥力的猜想。”

參考鏈接：
https://www.quantamagazine.org/new-math-measures-the-repulsive-force-within-polynomials-20200514/

Duffin-Schaeffer猜想被證

來自牛津大學的青年數(shù)學家詹姆斯·梅納德（James Maynard）攻下了困擾大家80年的數(shù)學難題——Duffin-Schaeffer猜想。

Duffin-Shaeffer猜想是度量丟番圖逼近中的一個重要猜想，由物理學家Richard Duffin和數(shù)學家Albert Schaeffer在1941年提出。

眾所周知，大部分的實數(shù)都是π、√2這樣的無理數(shù)，它們是無法用分數(shù)來表示的。

這個猜想假設 f：N→R≥0是具有正值的實值函數(shù)，只有當級數(shù)：

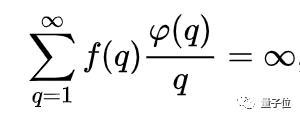
是發(fā)散的（q>0，φ(q)為歐拉函數(shù)，表示比q小且與q互質的正整數(shù)的個數(shù)），對于無理數(shù) α 而言，就存在無窮多個有理數(shù)，滿足不等式 | α-(p/q) |< f(q)/q。

這個證明過程困擾數(shù)學家數(shù)年，James Maynard和蒙特利爾大學的Dimitris Koukoulopoulos將它攻破了。

在他們的證明中，他們用分母創(chuàng)建了一個圖：把分母繪制成圖上的點，如果兩個點有許多共同的質因數(shù)，就用線將兩點連接起來。

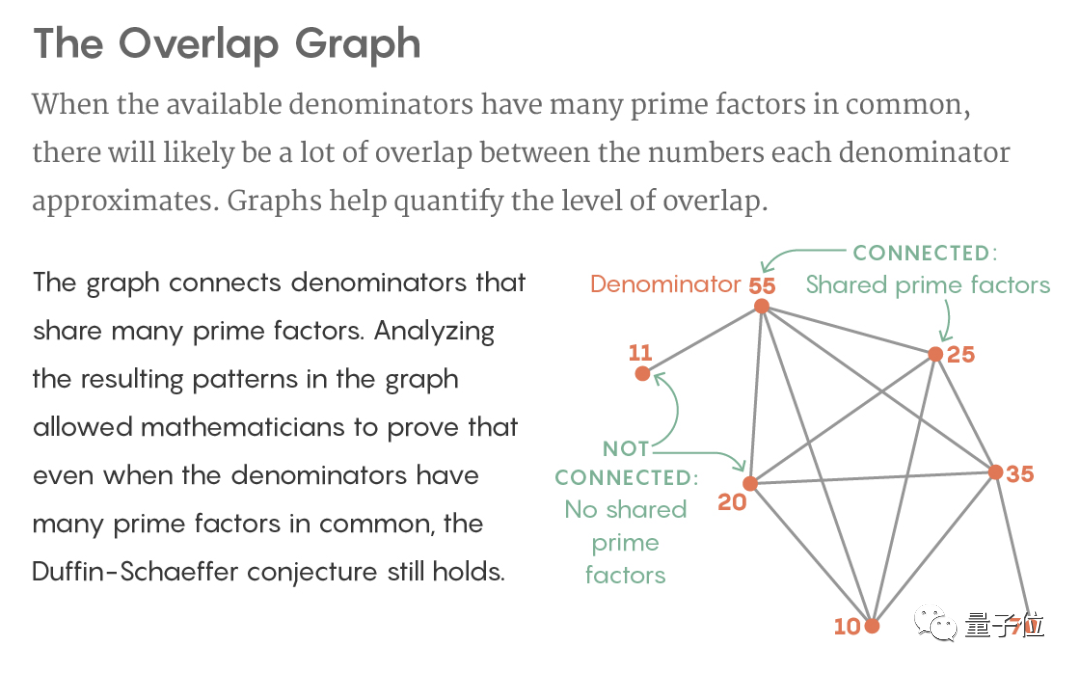
這樣一來，圖的結構就編碼了每個分母所近似的無理數(shù)之間的重疊。原本這種重合度是難以直接測定的。

由此，他們證明了Duffin-Schaeffer猜想的正確性。

閱讀延伸：
https://mp.weixin.qq.com/s/vsjFvYZBfYdGf7NM4TgRqg

以上就是Quanta Magazine評選出來的，今年計算機-數(shù)學領域最重要的幾項研究進展。

你認為這里面，哪些研究更有學術價值？

又或者說，是否還有沒上榜單的，但同樣是今年重大的研究突破？