[[418456]]

本文來自 李宏毅機器學習筆記 （LeeML-Notes） 組隊學習， 詳細介紹了使用深度學習技術的三大主要步驟。

教程地址：https://github.com/datawhalechina/leeml-notes

深度學習的三個步驟：

Step1：神經網絡（Neural network）

Step2：模型評估（Goodness of function）

Step3：選擇最優函數（Pick best function）

Step1：神經網絡

神經網絡是由很多單元連接而成，這些單元稱為神經元。

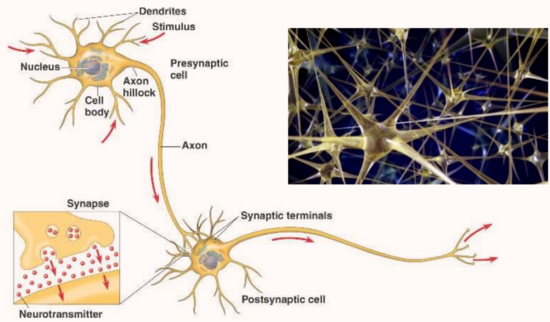
神經網絡類似于人類的神經細胞，電信號在神經元上傳遞，類似于數值在神經網絡中傳遞的過程。

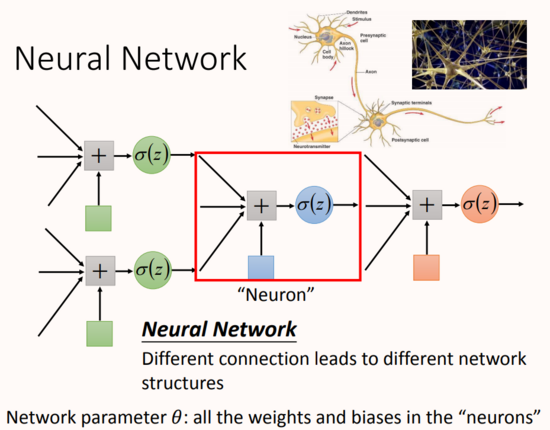
在這個神經網絡里面，一個神經元就相當于一個邏輯回歸函數，所以上圖中有很多邏輯回歸函數，其中每個邏輯回歸都有自己的權重和自己的偏差，這些權重和偏差就是參數。

圖中紅框表示的就是神經元，多個神經元以不同的方式進行連接，就會構成不同結構神經網絡。神經元的連接方式是由人工設計的。

• 神經元：神經元的結構，如圖所示

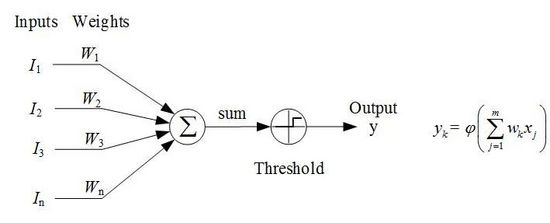
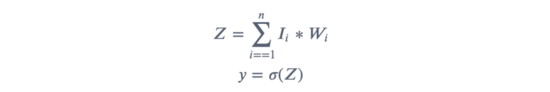
1. 每個 輸入 乘以其對應的 權重 ，將結果 求和 ，得到 ；

2. 將和代入 激活函數 ，得到結果 。

全連接前饋神經網絡

全連接：每一個神經元的輸出都連接到下一層神經元的每一個神經元，每一個神經元的輸入都來自上一層的每一個神經元。

前饋：前饋（feedforward）也可以稱為前向，從信號流向來理解就是輸入信號進入網絡后，信號流動是單向的，即信號從前一層流向后一層，一直到輸出層，其中任意兩層之間的連接并沒有反饋（feedback），亦即信號沒有從后一層又返回到前一層。

• 全連接前饋神經網絡示例：

如圖所示，這是一個4層的全連接神經網絡，每一層有兩個神經元，每個神經元的激活函數都是sigmoid。

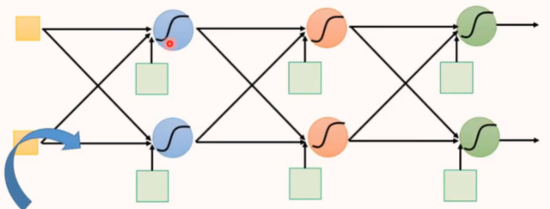
• 網絡輸入為(1, -1)，激活函數為sigmoid：

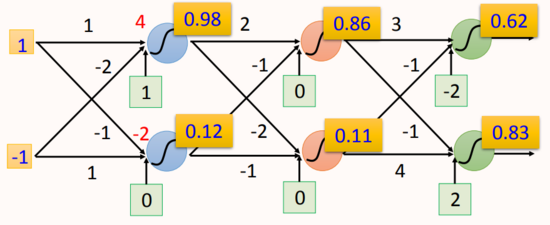
• 網絡輸入為(0, 0)，激活函數為sigmoid：

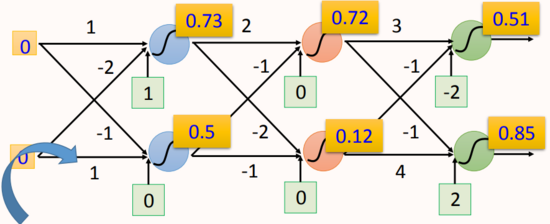
神經網絡結構：

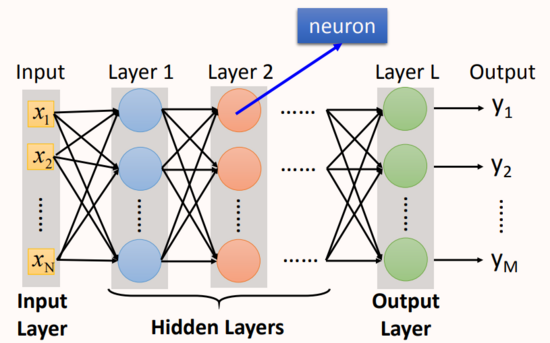
Input Layer：網絡的輸入層，Layer的size和真實輸入大小匹配。

Hidden Layers：處于輸入層和輸出層之間的網絡層。

• 為什么叫「 全連接 」？

  因為網絡中相鄰的兩層神經元，前一層的每一個神經元和后一層的每一個神經元都有連接，所以叫做全連接；

• 為什么叫「前饋」？

  因為值在網絡中傳遞的方向是由前往后傳（輸入層傳向輸出層），所以叫做Feedforward。

• Deep Learning，“Deep”體現在哪里？

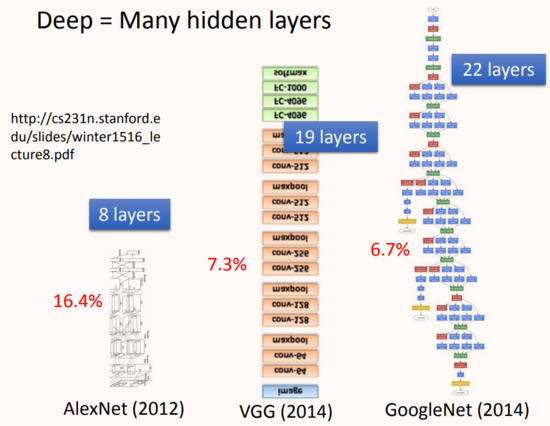
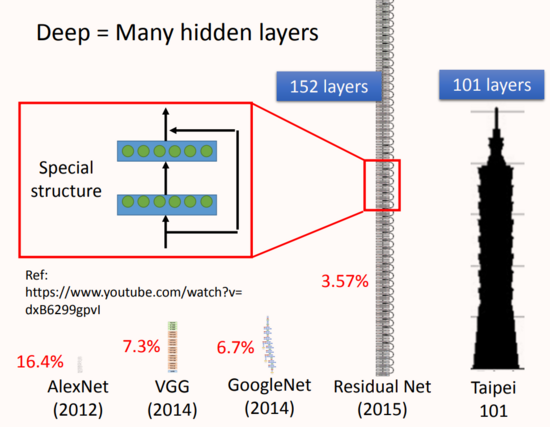
神經網絡的連接方式由人工設計，所以可以堆疊很多層神經元構成很“深”網絡，如上圖所示2015年提出的ResNet就達到了152層的深度。

深度神經需要特殊的訓練技巧

隨著層數變多，網絡參數增多，隨之運算量增大，通常都是超過億萬級的計算。對于這樣復雜的結構，我們一定不會一個一個的計算，對于億萬級的計算，使用loop循環效率很低。

網絡的運算過程如圖所示：

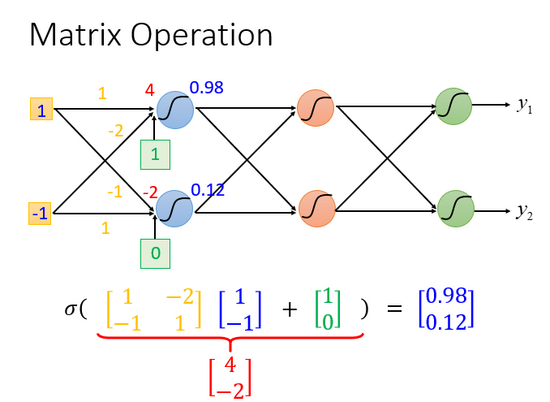
上圖中，網絡的運算過程可看作是矩陣的運算。

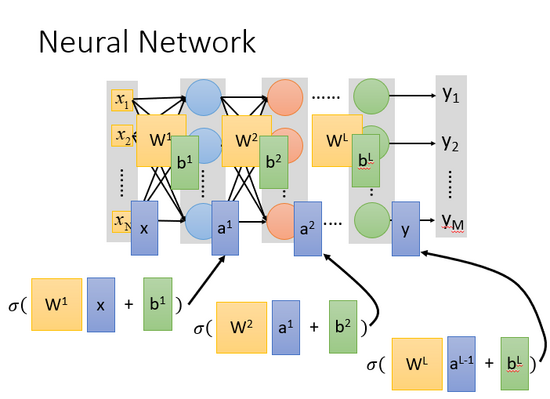
網絡的計算方法就像是嵌套，所以整個神經網絡運算就相當于一連串的矩陣運算。

從結構上看每一層的計算都是一樣的，也就是用計算機進行并行矩陣運算。這樣寫成矩陣運算的好處是，你可以使用GPU加速，GPU核心多，可以并行做大量的矩陣運算。

神經網絡的本質：通過隱藏層進行特征轉換

隱藏層可以看作是對網絡輸入層輸入特征進行特征處理，在最后一層隱藏層進行輸出，這時的輸出可以看作一組全新的特征，將其輸出給輸出層，輸出層對這組全新的特征進行分類。

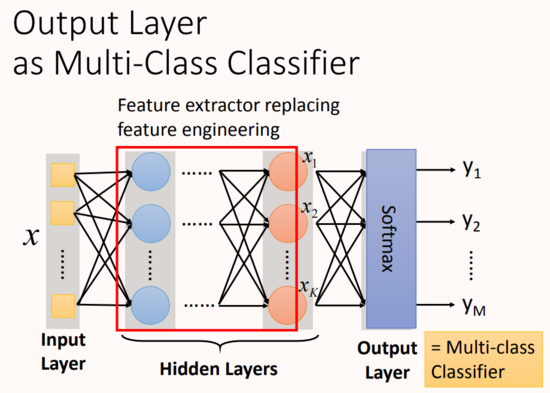
舉例：手寫數字識別

舉一個手寫數字體識別的例子：

輸入：一個16*16=256維的向量，每個pixel對應一個dimension，有顏色用（ink）用1表示，沒有顏色（no ink）用0表示，將圖片展平為一個256維的向量作為網絡輸入。

輸出：10個維度，每個維度代表一個數字的置信度（可理解為是該數字的概率有多大）

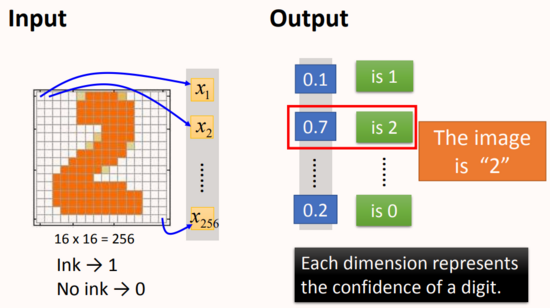
從輸出結果來看，每一個維度對應輸出一個數字，代表模型輸出為當前分類數字的概率。說明這張圖片是2的可能性就是最大的。

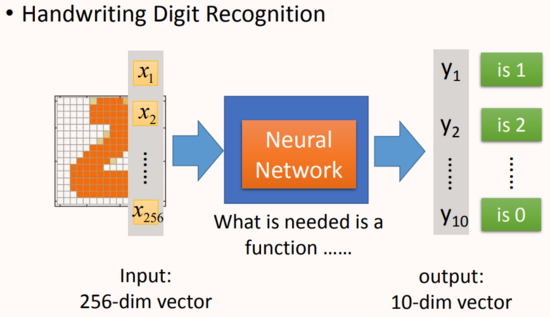
在這個問題中，唯一確定的就是，輸入是256維的向量，輸出是10維的向量，我們所需要找的函數就是輸入和輸出之間的神經網絡這個函數。

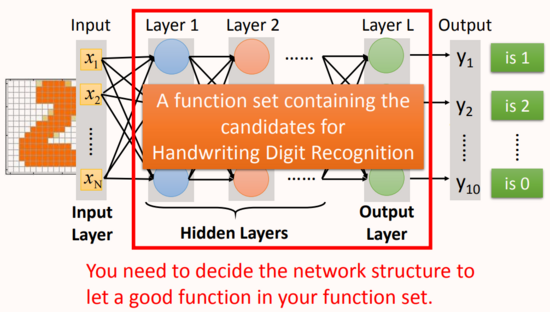
從上圖看神經網絡的結構決定了函數集（function set），通常來講函數集中的函數越多越復雜，網絡的表達空間就越大，越能handle復雜的模式，所以說網絡結構（network structured）很關鍵。

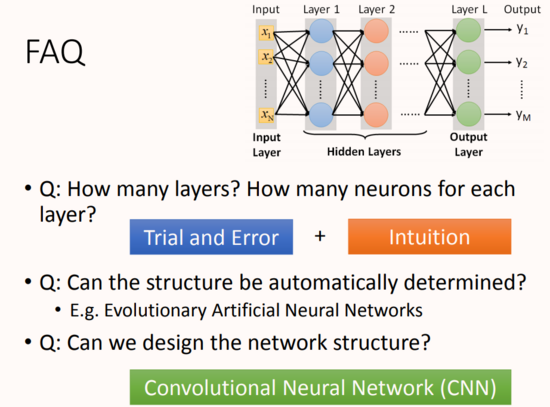
接下來有幾個問題：

• 多少層？每層有多少神經元？這個問我們需要用嘗試加上直覺的方法來進行調試。對于有些機器學習相關的問題，我們一般用特征工程來提取特征，但是對于深度學習，我們只需要設計神經網絡模型來進行就可以了。對于語音識別和影像識別，深度學習是個好的方法，因為特征工程提取特征并不容易。

• 結構可以自動確定嗎？有很多設計方法可以讓機器自動找到神經網絡的結構的，比如進化人工神經網絡（Evolutionary Artificial Neural Networks）但是這些方法并不是很普及 。

• 我們可以設計網絡結構嗎？可以的，比如 CNN卷積神經網絡（Convolutional Neural Network ）

Step2：模型評估

損失示例

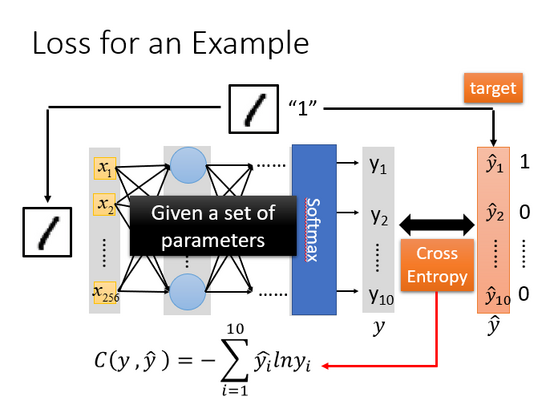
對于模型的評估，我們一般采用損失函數來反應模型的優劣，所以對于神經網絡來說，我們可以采用交叉熵（cross entropy）函數來對  和 ̂ 的損失進行計算，接下來我們就通過調整參數，讓交叉熵越小越好。

總體損失

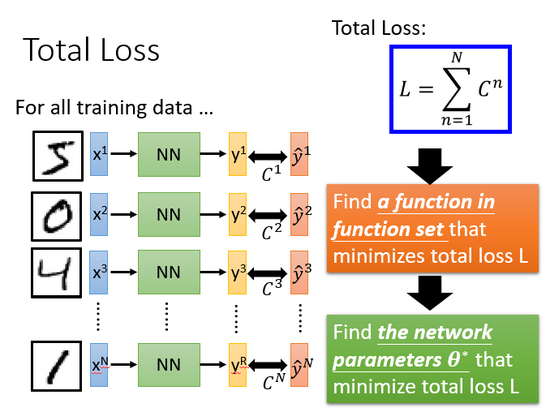
對于損失，我們不單單要計算一筆數據的，而是要計算整體所有訓練數據的損失，然后把所有的訓練數據的損失都加起來，得到一個總體損失 。接下來就是在functon set里面找到一組函數能最小化這個總體損失 ，或者是找一組神經網絡的參數 ，來最小化總體損失 。

Step3：選擇最優函數

如何找到最優的函數和最好的一組參數?

——使用梯度下降。

具體流程： 是一組包含權重和偏差的參數集合，隨機找一個初始值，接下來計算一下每個參數對應的偏微分，得到的一個偏微分的集合∇ 就是梯度，有了這些偏微分，我們就可以更新梯度得到新的參數，這樣不斷反復進行，就能得到一組參數使得損失函數的值最小。

反向傳播

在神經網絡訓練中，我們需要將計算得到的損失向前傳遞，以計算各個神經元連接的權重對損失的影響大小，這里用到的方法就是反向傳播。我們可以用很多框架來進行計算損失，比如說TensorFlow，Pytorch，theano等。

思考題

為什么要用深度學習，深層架構帶來哪些好處？那是不是隱藏層越多越好？

隱藏層越多越好？

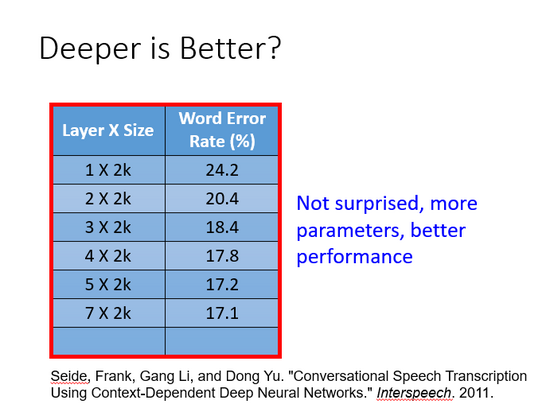
從圖中展示的結果看，毫無疑問，理論上網絡的層次越深效果越好，但現實中是這樣嗎？

普遍性定理

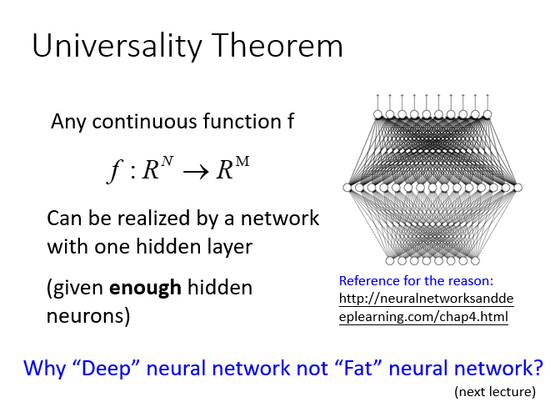
參數更多的模型擬合數據效果更好是很正常的。

有一個通用的理論：對于任何一個連續的函數，都可以用足夠多的神經元來表示。那為什么我們還需要深度(Deep)神經網絡結構呢，是不是直接用一層包含很多神經元的網絡(Fat)來表示就可以了？