1996年的8月19日至23日，芬蘭的瓦薩舉行了由芬蘭人工智能協會和瓦薩大學組織的芬蘭人工智能會議。

會議上發表的一篇論文證明：圖靈機就是一個循環神經網絡。

沒錯，這是在26年前！

讓我們來看一看，這篇發表于1996年的論文。

1 前言

1.1 神經網絡分類

神經網絡可用于分類任務，判斷輸入模式是否屬于特定的類別。

長期以來，人們都知道單層前饋網絡只能用于對線性可分的模式進行分類，即連續層越多，類的分布就越復雜。

當在網絡結構中引入反饋時，感知器輸出值被循環利用，連續層的數量原則上變為無限大。

算力有沒有質的提升？答案是肯定的。

例如，可以構造一個分類器來判斷輸入整數是否為素數。

事實證明，用于此目的的網絡大小可以是有限的，即使輸入整數大小不受限制，可以正確分類的素數數量也是無限的。

在本文中，「由相同計算元素組成的循環網絡結構」可用于完成任何（算法上的）可計算功能。

1.2 關于可計算性

根據可計算性理論的基本公理，可以使用圖靈機實現可計算函數，有多種方法可以實現圖靈機。

定義程序語言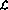。該語言有四種基本操作：

這里，V代表任何具有正整數值的變量，j代表任何行號。

可以證明，如果一個函數是圖靈可計算的，則可以使用這種簡單的語言對其進行編碼（有關詳細信息，請參見[1]）。

2 圖靈網絡

2.1 遞歸神經網絡結構

本文研究的神經網絡由感知器組成，它們都具有相同的結構，感知器數q的運算可以定義為

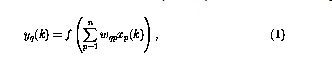
其中，當前時刻的感知器輸出（用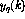表示）是使用n輸入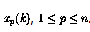計算的。

非線性函數f現在可定義為

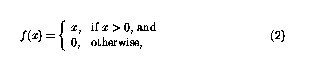
這樣函數就可以簡單地「切斷」負值，感知器網絡中的循環意味著感知器可以以復雜的方式組合。

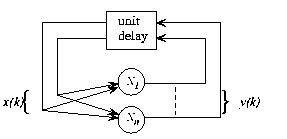
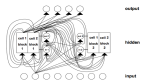
圖1 遞歸神經網絡的整體框架，結構自主無外部輸入，網絡行為完全由初始狀態決定

在圖1中，遞歸結構顯示在一個通用框架中：現在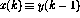和n是感知器的數量，從感知器p到感知器q的連接由（1）中的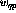標量權重表示。

即給定初始狀態，網絡狀態會迭代到不再發生變化，結果可以在該穩定狀態或網絡的「固定點」下讀取。

2.2 神經網絡建構

接下來闡述該程序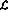如何在感知器網絡中實現。該網絡由以下節點（或感知器）組成：

• 對于程序中的每個變量V，都有一個變量節點。
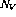• 對于每個程序行i，都有一個指令節點。
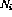• 對于第i行上的每個條件分支指令，另外還有兩個轉移節點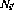和。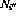

語言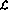程序的實現包括感知器網絡的以下變化：

• 對于程序中的每個變V，使用以下鏈接擴充網絡：

• 如果程序代碼的第i行沒有操作(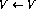)，則使用以下鏈接擴充網絡（假設該節點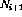存在：

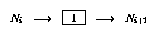
• 如果第i行有增量操作(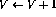)，則按如下方式擴充網絡：

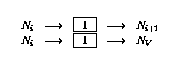
• 如果第i行有遞減操作(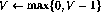)，則按如下方式擴充網絡：

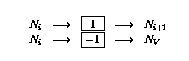
• 如果第i行有條件分支(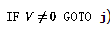)，則按如下方式擴充網絡：

2.3 等效性證明

現在需要證明的是，「網絡的內部狀態或網絡節點的內容」，可以用程序狀態來標識，同時網絡狀態的連續性與程序流對應。

定義網絡的「合法狀態」如下：

• 至所有轉換節點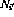和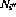（如2.2中所定義）的輸出為零()；
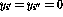• 至多一個指令節點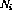有單位輸出(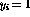)，所有其他指令節點有零輸出，并且
• 變量節點具有非負整數輸出值。

如果所有指令節點的輸出均為零，則狀態最終狀態。一個合法的網絡狀態可以直接解釋為一個程序「快照」——如果?，程序計數器在第i行，相應的變量值存儲在變量節點中。

網絡狀態的變化是由非零節點激活的。

首先，關注變量節點，事實證明它們表現為積分器，節點的先前內容被循環回同一節點。

從變量節點到其他節點的唯一連接具有負權重——這就是為什么包含零的節點不會改變，因為非線性的原因（2）。

接下來，詳細說明指令節點。假設唯一的非零指令節點?在時間k---這對應于程序計數器在程序代碼中第i行。

若程序中第i行是?，則網絡向前一步的行為可表示為（只顯示受影響的節點）

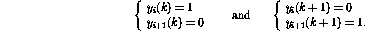
事實證明，新的網絡狀態再次合法。與程序代碼相比，這對應于程序計數器被轉移到第i+1行。

另一方面，如果程序中的第i行是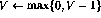，則向前一步的行為是

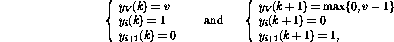
這樣，除了將程序計數器轉移到下一行之外，變量V的值也會遞減。如果第i行是

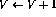，網絡的操作將是相同的，除了變量V的值增加。

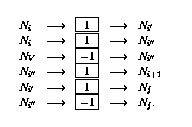
第i行的條件分支操作（IF 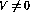 GOTO j）激活更復雜的操作序列：

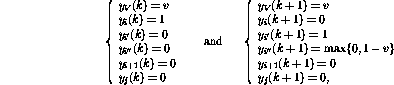
最后，

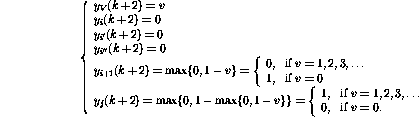
事實證明，在這些步驟之后，網絡狀態可以再次被解釋為另一個程序快照。

變量值已更改，token已轉移到新位置，就像執行了相應的程序行一樣。

如果token消失，網絡狀態不再改變——這只有在程序計數器「超出」程序代碼時才會發生，這意味著程序終止。

網絡的運行也類似對應程序的運行，證明完成。

3 修改

3.1 擴展

定義額外的流線型指令很容易，這些指令可以使編程更容易，并且生成的程序更具可讀性和執行速度。例如，

• 第i行的無條件分支（GOTO j）可以實現為
  ?
• 將常量c添加到第i行的變量（?）可以實現為
  ?
• 行i上的另一種條件分支（IF V=0 GOTO j ）可以實現為
  ?
• 此外，可以同時評估各種遞增/遞減指令。假設要執行以下操作：?。只需要一個節點?：
  ?

上述方式絕不是實現圖靈機的唯一途徑。

這是一個簡單的實現，在應用程序中不一定是最佳的。

3.2 矩陣制定

上述構造也可以以矩陣的形式實現。

基本思想是將變量值和「程序計數器」存儲在進程狀態s中，并讓狀態轉換矩陣A代表節點之間的鏈接。

矩陣結構的運算可以定義為一個離散時間的動態過程

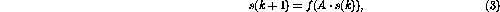
其中非線性向量值函數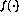現在按元素定義，如（2）中所示。

狀態轉移矩陣A的內容很容易從網絡公式中解碼出來——矩陣元素是節點之間的權重。

該矩陣公式類似于[3]中提出的「概念矩陣」框架。

4 例子

假設要實現一個簡單的函數y=x，也就是說，輸入變量x的值應該傳遞給輸出變量y。使用語言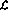可以將其編碼為（讓「入口點」現在不是第一行而是第三行）：

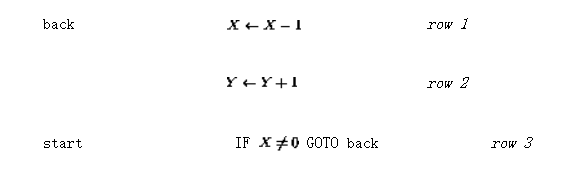
生成的感知器網絡如圖2所示。

實線代表正連接（權重為1），虛線代表負連接（權重-1）。與圖1相比，重新繪制了網絡結構，并通過在節點中集成延遲元件來簡化網絡結構。

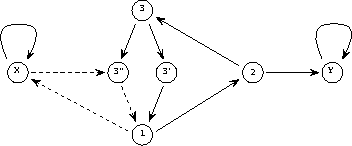
圖2 簡單程序的網絡實現

在矩陣形式中，上面的程序看起來像

矩陣A中的前兩行/列對應于連接到代表兩個變量Y和X的節點的鏈接，接下來的三行代表三個程序行（1、2和3），最后兩個代表分支指令所需的附加節點（3'和3''）。

然后是初始（迭代前）和最終（迭代后，找到固定點時）的狀態

如果變量節點的值將嚴格保在0和1之間，則動態系統（3）的操作將是線性的，該函數?根本沒有影響。

原則上，然后可以在分析中使用線性系統理論。

例如，在圖3中，示出了狀態轉移矩陣A的特征值。

即使在上面的例子中單位圓外有特征值，非線性使得迭代總是穩定的。

事實證明，迭代總是在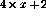步驟之后收斂，其中。

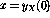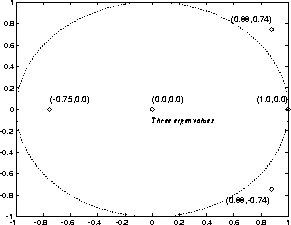
圖3 簡單程序的「特征值」

5 討論

5.1 理論方面

結果表明，圖靈機可以編碼為感知器網絡。

根據定義，所有可計算函數都是圖靈可計算的——在可計算性理論的框架內，不存在更強大的計算系統。

這就是為什么，可以得出結論——

循環感知器網絡（如上所示）是圖靈機的（又一種）形式。

這種等價的好處是可計算性理論的結果很容易獲得——例如，給定一個網絡和一個初始狀態，就不可能判斷這個過程最終是否會停止。

上述理論等價性并沒有說明計算效率的任何信息。

與傳統的圖靈機實現（實際上是今天的計算機）相比，網絡中發生的不同機制可以使一些功能在這個框架中更好地實現。

 至少在某些情況下，例如，一個算法的網絡實現可以通過允許snapshot向量中的多個「程序計數器」來被并行化。

網絡的運行是嚴格本地的，而不是全局的。

一個有趣的問題出現了，例如，是否可以在網絡環境中更有效地攻擊NP完全問題！

與語言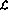相比，網絡實現具有以下「擴展」：

• 變量可以是連續的，而不僅僅是整數值。實際上，呈現實數的（理論）能力使網絡實現比語言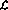更強大，所有以語言呈現的數字都是有理數。
• 可以同時存在各種「程序計數器」，并且控制的轉移可能是「模糊的」，這意味著指令節點提供的程序計數器值可能是非整數。
• 一個較小的擴展是可自由定義的程序入口點。這可能有助于簡化程序——例如，變量的復制在上面的三個程序行中完成，而名義解決方案（參見[1]）需要七行和一個額外的局部變量。

與原始程序代碼相比，矩陣公式顯然是比程序代碼更「連續」的信息表示形式——可以（經常）修改參數，而迭代結果不會突然改變。

這種「冗余」也許可以在某些應用中使用。

例如，當使用遺傳算法（GA）進行結構優化時，可以使遺傳算法中使用的隨機搜索策略更加高效：在系統結構發生變化后，可以搜索連續成本函數的局部最小值使用一些傳統技術（參見[4]）。

通過示例學習有限狀態機結構，如[5]中所述，可以知道：在這種更復雜的情況下也采用迭代增強網絡結構的方法。

不僅神經網絡理論可能受益于上述結果——僅看動態系統公式（3），很明顯，在可計算性理論領域發現的所有現象也都以簡單的形式存在——尋找非線性動態過程。

例如，停機問題的不可判定性是系統論領域的一個有趣貢獻：對于任何表示為圖靈機的決策過程，都存在形式（3）的動態系統，它違背了這個過程——對于例如，無法構建通用的穩定性分析算法。

5.2 相關工作

所呈現的網絡結構與遞歸來Hopfield神經網絡范式之間存在一些相似之處（例如，參見[2]）。

在這兩種情況下，「輸入」都被編碼為網絡中的初始狀態，「輸出」在迭代后從網絡的最終狀態中讀取。

Hopfield網絡的固定點是預編程的模式模型，輸入是「噪聲」模式——該網絡可用于增強損壞的模式。

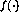中非線性函數的展望（2）使得上述「圖靈網絡」中可能的狀態數量是無限的。

與單元輸出始終為-1或1的Hopfield網絡相比，可以看出，理論上，這些網絡結構有很大不同。

例如，雖然Hopfield網絡中的穩定點集是有限的，但以圖靈網絡為代表的程序通常具有無限數量的可能結果。

Hopfield網絡的計算能力在[6]中進行了討論。

Petri網是基于事件和并發系統建模的強大工具[7]。

Petri網由位和轉移以及連接它們的弧組成。每個地方可能包含任意數量的token，token的分布稱為Petri網的標記。

如果轉換的所有輸入位置都被標記占用，則轉換可能會觸發，從每個輸入位置刪除一個標記，并向其每個輸出位置添加一個標記。

可以證明，具有附加抑制弧的擴展Petri網也具有圖靈機的能力（參見[7]）。

上述圖靈網與Petri網的主要區別在于Petri網的框架更為復雜，具有專門定制的結構，不能用簡單的一般形式（3）來表達。

參考

1 Davis, M. and Weyuker, E.: Computability, Complexity, and Languages---Fundamentals of Theoretical Computer Science. Academic Press, New York, 1983.

2 Haykin, S.: Neural Networks. A Comprehensive Foundation. Macmillan College Publishing, New York, 1994.

3 Hy?tyniemi, H.: Correlations---Building Blocks of Intelligence? In ?lyn ulottuvuudet ja oppihistoria (History and dimensions of intelligence), Finnish Artificial Intelligence Society, 1995, pp. 199--226.

4 Hy?tyniemi, H. and Koivo, H.: Genes, Codes, and Dynamic Systems. In Proceedings of the Second Nordic Workshop on Genetic Algorithms (NWGA'96), Vaasa, Finland, August 19--23, 1996.

5 Manolios, P. and Fanelli, R.: First-Order Recurrent Neural Networks and Deterministic Finite State Automata. Neural Computation 6, 1994, pp. 1155--1173.

6 Orponen, P.: The Computational Power of Discrete Hopfield Nets with Hidden Units. Neural Computation 8, 1996, pp. 403--415.

7 Peterson, J.L.: Petri Net Theory and the Modeling of Systems. Prentice--Hall, Englewood Cliffs, New Jersey, 1981.

參考資料：

??http://users.ics.aalto.fi/tho/stes/step96/hyotyniemi1/???