機(jī)器學(xué)習(xí)與微分方程的淺析
大家都已經(jīng)使用機(jī)器學(xué)習(xí)了,尤其是基于神經(jīng)網(wǎng)絡(luò)的深度學(xué)習(xí),chatGPT甚囂塵上,還需要深入理解微分方程么?不論答案是啥,都會(huì)涉及到二者的對(duì)比,那么,機(jī)器學(xué)習(xí)與微分方程的區(qū)別又是什么呢?
從愛(ài)情模型的微分方程說(shuō)起
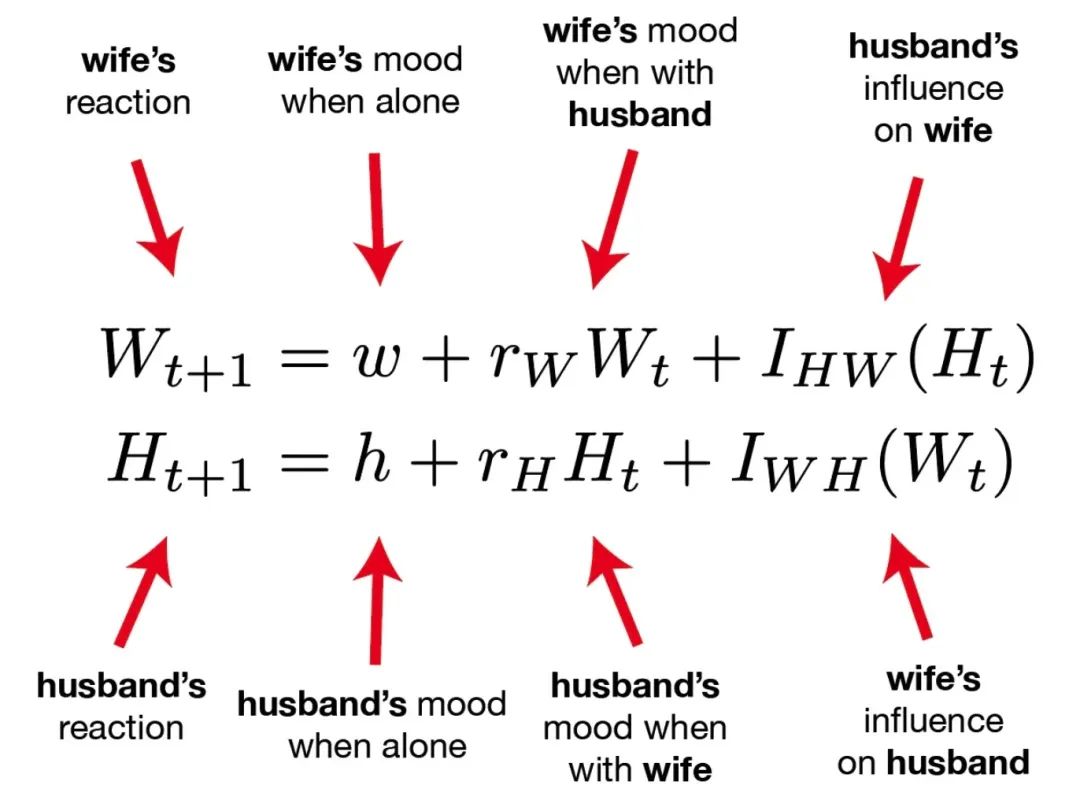
這兩個(gè)方程預(yù)測(cè)了夫妻戀愛(ài)關(guān)系的長(zhǎng)久性,基于心理學(xué)家 John Gottman 的開(kāi)創(chuàng)性工作,該模型預(yù)測(cè)持續(xù)的積極情緒是婚姻成功的有力因素。關(guān)于模型的更多解讀,可以參考《幸福的婚姻》一書(shū),作者還給出了維護(hù)婚姻幸福的7個(gè)法則:
- 完善你的愛(ài)情地圖
- 培養(yǎng)你對(duì)配偶的喜愛(ài)和贊美
- 彼此靠近而不是遠(yuǎn)離
- 讓配偶影響你的決定
- 以溫和開(kāi)場(chǎng),用妥協(xié)收?qǐng)?/li>
- 學(xué)會(huì)和問(wèn)題和諧相處
- 創(chuàng)造共同意義
疫情三年,大家親身經(jīng)歷,冷暖自知。那么,如何用微分方程描述患者與傳染者的關(guān)系呢?
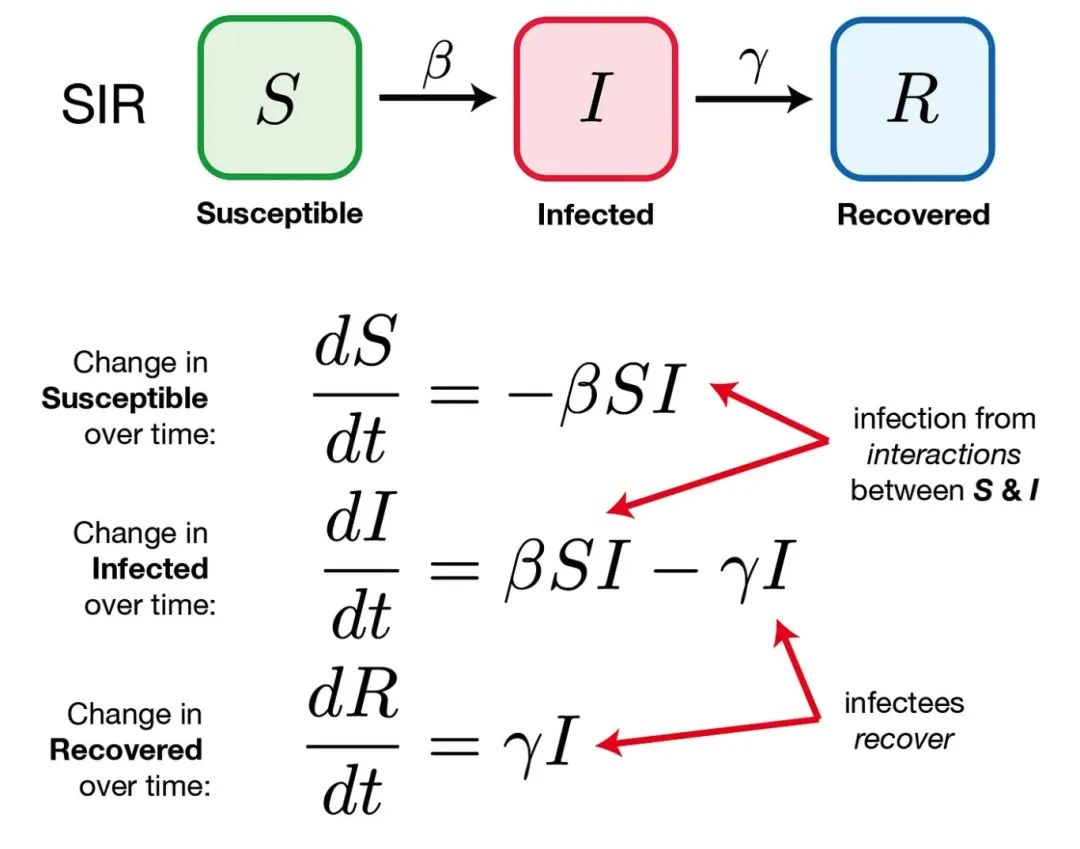
SIR 模型假設(shè)病毒是通過(guò)感染者和未感染者之間的直接接觸傳播的,患病者自動(dòng)以某種固定的速率恢復(fù)。
這些微分方程都包含了一些未知函數(shù)的導(dǎo)數(shù)(即變化率),這些未知函數(shù),例如 SIR 模型中的 S (t) ,I (t)和 R (t) ,稱(chēng)為該微分方程的解。基于這些方程的機(jī)制,我們可以得到模型的設(shè)計(jì)方式,而數(shù)據(jù)稍后將用于驗(yàn)證我們的假設(shè)。
數(shù)學(xué)模型的分類(lèi)
類(lèi)似微分方程這樣的數(shù)學(xué)模型是預(yù)先對(duì)系統(tǒng)的基本機(jī)制進(jìn)行假設(shè),建模始于物理學(xué),實(shí)際上,整個(gè)數(shù)學(xué)建模領(lǐng)域都始于17世紀(jì)對(duì)解開(kāi)行星運(yùn)動(dòng)背后的基本動(dòng)力學(xué)的探索。從那時(shí)起,基于數(shù)學(xué)的機(jī)制模型開(kāi)啟了許多現(xiàn)象的關(guān)鍵見(jiàn)解,從生物學(xué)和工程學(xué)到經(jīng)濟(jì)學(xué)以及社會(huì)科學(xué)。這樣的機(jī)制模型可以分為基于方程的模型 ,如微分方程,或基于Agent的模型。
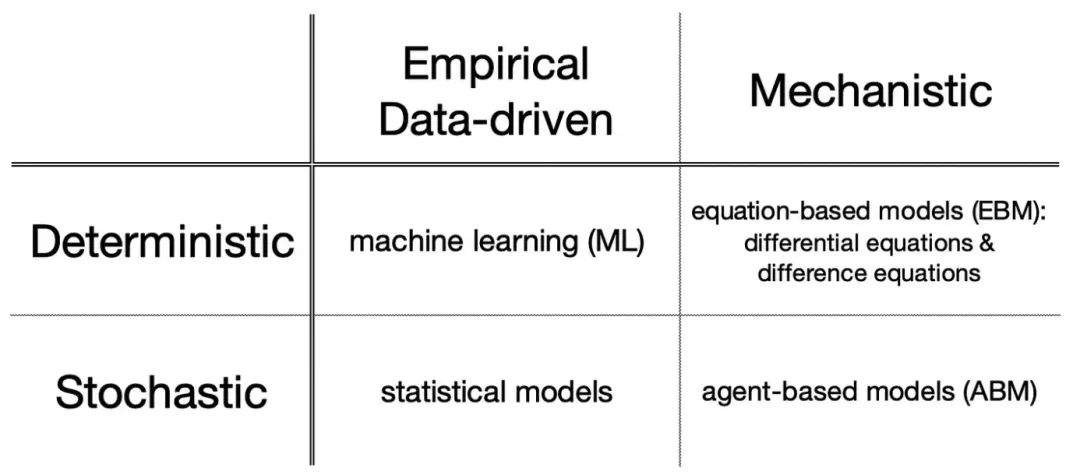
基于經(jīng)驗(yàn)或數(shù)據(jù)驅(qū)動(dòng)的建模,例如機(jī)器學(xué)習(xí),是通過(guò)豐富的數(shù)據(jù)來(lái)了解系統(tǒng)的結(jié)構(gòu)。機(jī)器學(xué)習(xí)對(duì)于復(fù)雜的系統(tǒng)特別有用,因?yàn)槲覀冋娴牟恢廊绾螐脑肼曋蟹蛛x出信號(hào),這時(shí)候,只要訓(xùn)練一個(gè)聰明的算法就可以幫助解決難題。
機(jī)器學(xué)習(xí)任務(wù)可大致分為以下幾類(lèi):
- 監(jiān)督式學(xué)習(xí)(例如,回歸和分類(lèi)) ;
- 非監(jiān)督式學(xué)習(xí)(例如,聚類(lèi)及降維) ;
- 強(qiáng)化學(xué)習(xí)
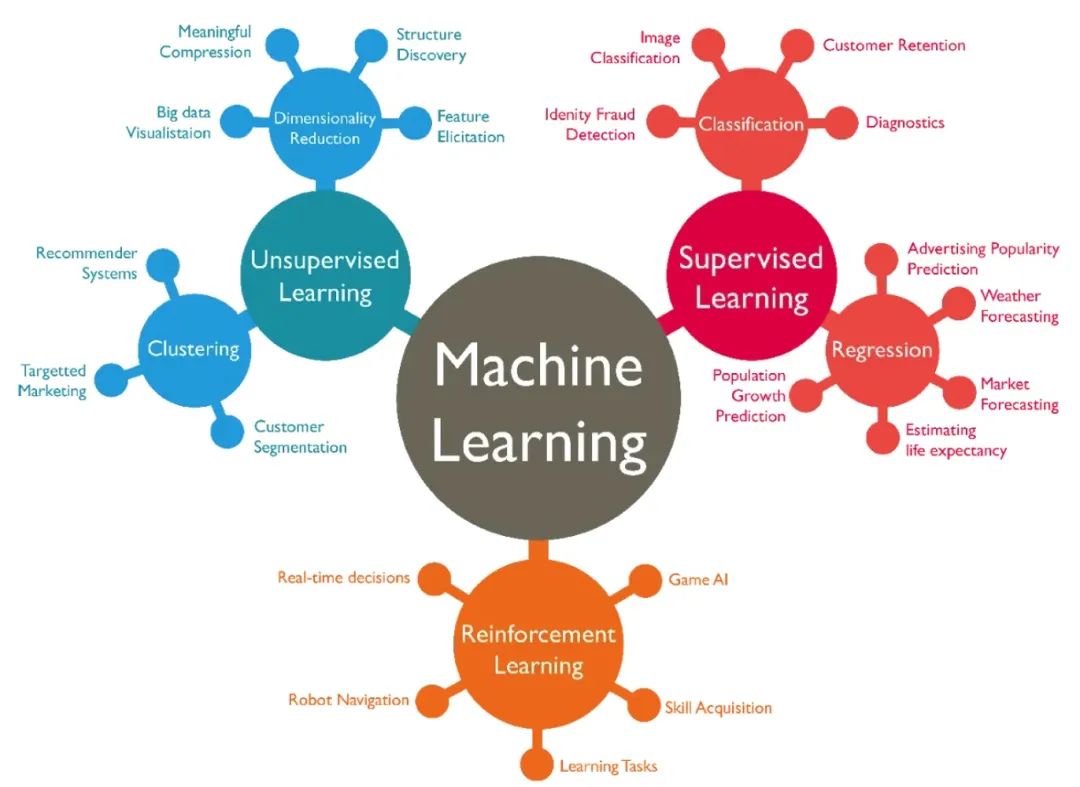
先進(jìn)的機(jī)器學(xué)習(xí)和人工智能系統(tǒng)如今在我們的日常生活中無(wú)處不在,從基于智能音箱的會(huì)話(huà)助手(例如 小度)到 各種推薦引擎,再到人臉識(shí)別技術(shù),甚至特斯拉(Tesla)的自動(dòng)駕駛汽車(chē)。所有這些都是由嵌入在堆積如山的代碼下的數(shù)學(xué)和統(tǒng)計(jì)建模驅(qū)動(dòng)的。
進(jìn)一步,可以將這些模型分為“確定性”(預(yù)測(cè)是固定的)或“隨機(jī)性”(預(yù)測(cè)包括隨機(jī)性)的。
確定性模型忽略隨機(jī)變量,在相同的起始條件下總是預(yù)測(cè)相同的結(jié)果。一般的,機(jī)器學(xué)習(xí)和基于方程的模型都是確定性的,輸出總是可預(yù)測(cè)的。換句話(huà)說(shuō),輸出完全由輸入決定。
隨機(jī)模型通過(guò)在模型中引入概率來(lái)考慮總體的隨機(jī)變化。捕捉這些變化的一種方法是讓每個(gè)實(shí)體成為模型中一個(gè)單獨(dú)的Agent,并為這些Agent定義允許的行為和機(jī)制,這些行為和機(jī)制具有一定的概率。這些是基于Agent的模型。
然而,對(duì)個(gè)體行為者進(jìn)行建模的可實(shí)現(xiàn)性是有代價(jià)的,而基于代理的模型則更為現(xiàn)實(shí)。由于計(jì)算代價(jià)的高昂以模型的可解釋性,這激發(fā)了數(shù)學(xué)建模中的一個(gè)關(guān)鍵概念: 模型復(fù)雜度。
模型復(fù)雜度
模型復(fù)雜度的困境是所有建模者都要面對(duì)的現(xiàn)實(shí),我們的目標(biāo)是構(gòu)建并優(yōu)化既不太簡(jiǎn)單也不太復(fù)雜的模型。簡(jiǎn)單的模型容易分析,但往往缺乏預(yù)測(cè)能力。復(fù)雜的模型可能是超現(xiàn)實(shí)的,但有可能試圖了解復(fù)雜問(wèn)題的背后真相。
我們需要在簡(jiǎn)單性和易于分析性之間進(jìn)行權(quán)衡。復(fù)雜的機(jī)器學(xué)習(xí)模型在努力學(xué)習(xí)信號(hào)(即系統(tǒng)的真實(shí)結(jié)構(gòu))的同時(shí)排除噪音(即干擾)。這導(dǎo)致模型在新數(shù)據(jù)上表現(xiàn)不佳。換句話(huà)說(shuō),機(jī)器學(xué)習(xí)模型的普遍性較差。
平衡模型復(fù)雜度的微妙行為是一種“藝術(shù)”,試圖尋找一個(gè)既不太簡(jiǎn)單也不太復(fù)雜的最佳位置。這個(gè)理想的模型可以沖刷掉噪音,捕捉到正在發(fā)生的事情的潛在動(dòng)態(tài),并且是可以合理解釋的。
需要注意的是,這意味著一個(gè)好的數(shù)學(xué)模型并不總是正確的。不過(guò)沒(méi)關(guān)系。可推廣性是目標(biāo),可以向受眾解釋模型為什么這么做,無(wú)論他們是學(xué)者、工程師還是商業(yè)領(lǐng)袖。
所有的模型都是錯(cuò)誤的,但有些是有用的。——喬治?博克斯(George Box),1976
在機(jī)器學(xué)習(xí)和統(tǒng)計(jì)學(xué)中,模型復(fù)雜度稱(chēng)為偏差-方差的折衷。高偏差模型過(guò)于簡(jiǎn)單,導(dǎo)致擬合不足,而高方差模型記憶噪聲而不是信號(hào),導(dǎo)致過(guò)度擬合。數(shù)據(jù)科學(xué)家努力通過(guò)精心選擇訓(xùn)練算法和調(diào)整相關(guān)的超參數(shù)來(lái)達(dá)到這種微妙的平衡。
微分方程與機(jī)器學(xué)習(xí)的對(duì)比
在機(jī)制建模中,我們?cè)趯?duì)系統(tǒng)的潛在機(jī)制做出假設(shè)之前,會(huì)仔細(xì)地觀(guān)察和審查一種現(xiàn)象,然后用數(shù)據(jù)驗(yàn)證模型。我們的假設(shè)正確嗎?如果是這樣,既然是親自挑選的機(jī)制,完全可以向任何人解釋是什么模型的這種行為。如果假設(shè)是錯(cuò)誤的,那也沒(méi)關(guān)系,只是浪費(fèi)了一些時(shí)間,沒(méi)什么大不了的。建模畢竟是反復(fù)試驗(yàn)。修補(bǔ)這些假設(shè),甚至從頭開(kāi)始。機(jī)制模型,通常是微分方程等形式的方程,甚至是基于主體的模型。
在數(shù)據(jù)驅(qū)動(dòng)建模中,我們是先讓數(shù)據(jù)開(kāi)始工作,為我們構(gòu)建系統(tǒng)的全景。我們要做的就是滿(mǎn)足那臺(tái)機(jī)器的數(shù)據(jù)質(zhì)量,希望有足夠的數(shù)據(jù)。這便是機(jī)器學(xué)習(xí)。如果普通人很難搞清楚一個(gè)現(xiàn)象,可以調(diào)整一臺(tái)機(jī)器來(lái)篩選噪音,為我們學(xué)習(xí)那難以捉摸的信號(hào)。標(biāo)準(zhǔn)的機(jī)器學(xué)習(xí)任務(wù)包括回歸和分類(lèi),它們使用一系列度量標(biāo)準(zhǔn)進(jìn)行評(píng)估。神經(jīng)網(wǎng)絡(luò)和強(qiáng)化學(xué)習(xí)也已經(jīng)流行了起來(lái),它們能夠創(chuàng)建模型并學(xué)習(xí)令人驚嘆的復(fù)雜信號(hào)。
盡管機(jī)器學(xué)習(xí)從20世紀(jì)50年代就已經(jīng)存在,但隨著計(jì)算機(jī)變得越來(lái)越強(qiáng)大,數(shù)據(jù)在爆炸式增長(zhǎng),使得人們?nèi)绾卫萌斯ぶ悄塬@得競(jìng)爭(zhēng)優(yōu)勢(shì)、提高洞察力和增長(zhǎng)利潤(rùn)展開(kāi)了廣泛的實(shí)踐。對(duì)于不同的應(yīng)用場(chǎng)景,機(jī)器學(xué)習(xí)與微分方程都有著廣泛的場(chǎng)景。?