有網(wǎng)友評(píng)論，我也發(fā)明了一種排序算法，時(shí)間復(fù)制度為O(1)，稱為OD排序，基本思想如下：

• step 1 : 將待排序數(shù)據(jù)打包發(fā)給OD
• step 2 : IF  OD排序時(shí)間復(fù)雜度 > O(1), GOTO step 3。ELSE  GOTO step 4.
• step 3 : 先來(lái)一記寒冰掌，然后優(yōu)化
• step 4: 遙遙領(lǐng)先，官宣自主研發(fā)O(1)排序算法

今天我們就開(kāi)始學(xué)習(xí)如何分析、統(tǒng)計(jì)算法的執(zhí)行效率和資源消耗呢？請(qǐng)看本文一一道來(lái)。

數(shù)據(jù)結(jié)構(gòu)和算法本生解決的就是「快」和「省」的問(wèn)題，那就是如何讓代碼跑得快，還能節(jié)省存儲(chǔ)空間。

打造一臺(tái)法拉利，不僅跑得快還省油，擁有好的算法與數(shù)據(jù)結(jié)構(gòu)，程序跑得快，還省內(nèi)存并且長(zhǎng)時(shí)間運(yùn)行也不會(huì)出故障，就像跑車(chē)長(zhǎng)時(shí)間運(yùn)行車(chē)子也不會(huì)出現(xiàn)異常「車(chē)震」，同時(shí)還快。

所以趕緊上車(chē)，一起學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)與算法，趕緊上車(chē)「穩(wěn)穩(wěn)」的學(xué)會(huì)如何檢測(cè)跑車(chē)到底快不快，省油不省油。

這里就要用到我們今天要講的內(nèi)容：時(shí)間、空間復(fù)雜度分析。只要講到數(shù)據(jù)結(jié)構(gòu)與算法，就一定離不開(kāi)時(shí)間、空間復(fù)雜度分析。

復(fù)雜度分析是整個(gè)算法學(xué)習(xí)的精髓，只要掌握了它，數(shù)據(jù)結(jié)構(gòu)和算法的內(nèi)容基本上就掌握了一半。這就就像內(nèi)功心法，上乘武功還需搭配牛逼心法。

只有學(xué)會(huì)了檢測(cè)標(biāo)準(zhǔn)才能在設(shè)計(jì)的時(shí)候心中按照標(biāo)準(zhǔn)來(lái)編寫(xiě)打造我們的「法拉利」代碼。

為何需要復(fù)雜度分析

可能會(huì)有些疑惑，我把代碼跑一遍，通過(guò)統(tǒng)計(jì)、監(jiān)控，就能得到算法執(zhí)行的時(shí)間和占用的內(nèi)存大小。為什么還要做時(shí)間、空間復(fù)雜度分析呢？這種分析方法能比我實(shí)實(shí)在在跑一遍得到的數(shù)據(jù)更準(zhǔn)確嗎？

這種屬于非要自己去嘗試，沒(méi)有根據(jù)合理方法預(yù)測(cè)我們要的就是像算命大師一樣預(yù)先知道。很多數(shù)據(jù)結(jié)構(gòu)和算法書(shū)籍還給這種方法起了一個(gè)名字，叫事后統(tǒng)計(jì)法。但是，這種統(tǒng)計(jì)方法有非常大的局限性。

1. 測(cè)試結(jié)果非常依賴測(cè)試環(huán)境

測(cè)試環(huán)境中硬件的不同會(huì)對(duì)測(cè)試結(jié)果有很大的影響。比如，我們拿同樣一段代碼，分別用 Intel Core i7 處理器和 Intel Core i3 處理器來(lái)運(yùn)行，不用說(shuō)，i7 處理器要比 i3 處理器執(zhí)行的速度快很多。

就好像同一輛車(chē)放在深圳北環(huán)大道與我家農(nóng)村小山溝跑是不一樣的。

2.測(cè)試結(jié)果受數(shù)據(jù)規(guī)模的影響很大

后面我們會(huì)講排序算法，我們先拿它舉個(gè)例子。對(duì)同一個(gè)排序算法，待排序數(shù)據(jù)的有序度不一樣，排序的執(zhí)行時(shí)間就會(huì)有很大的差別。

極端情況下，如果數(shù)據(jù)已經(jīng)是有序的，那排序算法不需要做任何操作，執(zhí)行時(shí)間就會(huì)非常短。除此之外，如果測(cè)試數(shù)據(jù)規(guī)模太小，測(cè)試結(jié)果可能無(wú)法真實(shí)地反應(yīng)算法的性能。

比如，對(duì)于小規(guī)模的數(shù)據(jù)排序，插入排序可能反倒會(huì)比快速排序要快！

所以，我們需要一個(gè)不用具體的測(cè)試數(shù)據(jù)來(lái)測(cè)試，就可以粗略地估計(jì)算法的執(zhí)行效率的方法。這就是我們今天要講的時(shí)間、空間復(fù)雜度分析方法。

大 O 復(fù)雜度表示法

算法的執(zhí)行效率，粗略地講，就是算法代碼執(zhí)行的時(shí)間。但是，如何在不運(yùn)行代碼的情況下，用“肉眼”得到一段代碼的執(zhí)行時(shí)間呢？就像檢測(cè)車(chē)子馬力與油耗似的。

求 1,2,3…n 的累加和。現(xiàn)在，一起估算一下這段代碼的執(zhí)行時(shí)間。

int cal(int n) {
   int sum = 0;
   int i = 1;
   for (; i <= n; ++i) {
     sum = sum + i;
   }
   return sum;
 }

從 CPU 的角度來(lái)看，這段代碼的每一行都執(zhí)行著類似的操作：讀數(shù)據(jù)-運(yùn)算-寫(xiě)數(shù)據(jù)。盡管每行代碼對(duì)應(yīng)的 CPU 執(zhí)行的個(gè)數(shù)、執(zhí)行的時(shí)間都不一樣，但是，我們這里只是粗略估計(jì)，所以可以假設(shè)每行代碼執(zhí)行的時(shí)間都一樣，為 unit_time單位時(shí)間。

在這個(gè)假設(shè)的基礎(chǔ)之上，這段代碼的總執(zhí)行時(shí)間是多少呢？

第 2、3 行代碼分別需要 1 個(gè) unit_time 的執(zhí)行時(shí)間，第 4、5 行都運(yùn)行了 n 遍，所以需要 2n*unit_time 的執(zhí)行時(shí)間，所以這段代碼總的執(zhí)行時(shí)間就是 (2n+2)*unit_time。可以看出來(lái)，所有代碼的執(zhí)行時(shí)間 T(n) 與每行代碼的執(zhí)行次數(shù)成正比。

我們繼續(xù)分析下面這段代碼：

int cal(int n) {
   int sum = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1;
     for (; j <= n; ++j) {
       sum = sum +  i * j;
     }
   }
 }

我們依舊假設(shè)每個(gè)語(yǔ)句的執(zhí)行時(shí)間是 unit_time。那這段代碼的總執(zhí)行時(shí)間 T(n) 是多少呢？

第 2、3、4 行代碼，每行都需要 1 個(gè) unit_time 的執(zhí)行時(shí)間，第 5、6 行代碼循環(huán)執(zhí)行了 n 遍，需要 2n * unit_time 的執(zhí)行時(shí)間，第 7、8 行代碼循環(huán)執(zhí)行了 n^2^遍，所以需要 2n^2^ * unit_time 的執(zhí)行時(shí)間。所以，整段代碼總的執(zhí)行時(shí)間 T(n) = (2n^2^+ 2n + 3)*unit_time。

盡管我們不知道 unit_time 的具體值，但是通過(guò)這兩段代碼執(zhí)行時(shí)間的推導(dǎo)過(guò)程，我們可以得到一個(gè)非常重要的規(guī)律，那就是，==所有代碼的執(zhí)行時(shí)間 T(n) 與每行代碼的執(zhí)行次數(shù) n 成正比==。

我們可以把這個(gè)規(guī)律總結(jié)成一個(gè)公式。注意，大 O 就要登場(chǎng)了！

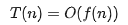
其中

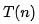
，我們已經(jīng)講過(guò)了，它表示代碼執(zhí)行的時(shí)間；n 表示數(shù)據(jù)規(guī)模的大小；

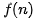
表示每行代碼執(zhí)行的次數(shù)總和。因?yàn)檫@是一個(gè)公式，所以用

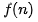
  來(lái)表示。公式中的 O，表示代碼的執(zhí)行時(shí)間 T(n) 與 f(n) 表達(dá)式成正比。

所以，第一個(gè)例子中的

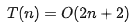
 ，第二個(gè)例子中的 T(n) = O(2n^2^+2n+3)。這就是大 O 時(shí)間復(fù)雜度表示法。

大 O 時(shí)間復(fù)雜度實(shí)際上并不具體表示代碼真正的執(zhí)行時(shí)間，而是表示代碼執(zhí)行時(shí)間隨數(shù)據(jù)規(guī)模增長(zhǎng)的變化趨勢(shì)，所以，也叫作漸進(jìn)時(shí)間復(fù)雜度（asymptotic time complexity），簡(jiǎn)稱時(shí)間復(fù)雜度。敲黑板了，表達(dá)的是變化趨勢(shì)，并不是真正的執(zhí)行時(shí)間。

當(dāng) n 很大時(shí)，你可以把它想象成 100000、1000000。而公式中的==低階、常量、系數(shù)==三部分并不左右增長(zhǎng)趨勢(shì)，所以都可以忽略。我們只需要記錄一個(gè)最大量級(jí)就可以了，如果用大 O 表示法表示剛講的那兩段代碼的時(shí)間復(fù)雜度，就可以記為：

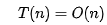
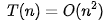
時(shí)間復(fù)雜度分析

前面介紹了大 O 時(shí)間復(fù)雜度的由來(lái)和表示方法。現(xiàn)在我們來(lái)看下，如何分析一段代碼的時(shí)間復(fù)雜度？有三個(gè)比較實(shí)用的方法可以分享。

1. 只關(guān)注循環(huán)執(zhí)行次數(shù)最多的一段代碼

大 O 這種復(fù)雜度表示方法只是表示一種變化趨勢(shì)。我們通常會(huì)忽略掉公式中的常量、低階、系數(shù)，只需要記錄一個(gè)最大階的量級(jí)就可以了。所以，我們?cè)诜治鲆粋€(gè)算法、一段代碼的時(shí)間復(fù)雜度的時(shí)候，也只關(guān)注循環(huán)執(zhí)行次數(shù)最多的那一段代碼就可以了。擒賊先擒王就是這么回事。

這段核心代碼執(zhí)行次數(shù)的 n 的量級(jí)，就是整段要分析代碼的時(shí)間復(fù)雜度。

int cal(int n) {
   int sum = 0;
   int i = 1;
   for (; i <= n; ++i) {
     sum = sum + i;
   }
   return sum;
 }

其中第 2、3 行代碼都是常量級(jí)的執(zhí)行時(shí)間，與 n 的大小無(wú)關(guān)，所以對(duì)于復(fù)雜度并沒(méi)有影響。

循環(huán)執(zhí)行次數(shù)最多的是第 4、5 行代碼，所以這塊代碼要重點(diǎn)分析。前面我們也講過(guò)，這兩行代碼被執(zhí)行了 n 次，所以總的時(shí)間復(fù)雜度就是 O(n)。

2. 加法法則：總復(fù)雜度等于量級(jí)最大的那段代碼的復(fù)雜度

看如下代碼可以先試著分析一下，然后再往下看跟我的分析思路是否一樣。

int cal(int n) {
   int sum_1 = 0;
   int p = 1;
   for (; p < 100; ++p) {
     sum_1 = sum_1 + p;
   }

   int sum_2 = 0;
   int q = 1;
   for (; q < n; ++q) {
     sum_2 = sum_2 + q;
   }

   int sum_3 = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1;
     for (; j <= n; ++j) {
       sum_3 = sum_3 +  i * j;
     }
   }

   return sum_1 + sum_2 + sum_3;
 }

這個(gè)代碼分為三部分，分別是求 sum_1、sum_2、sum_3。我們可以分別分析每一部分的時(shí)間復(fù)雜度，然后把它們放到一塊兒，再取一個(gè)量級(jí)最大的作為整段代碼的復(fù)雜度。

• 第一段的時(shí)間復(fù)雜度是多少呢？這段代碼循環(huán)執(zhí)行了 100 次，所以是一個(gè)常量的執(zhí)行時(shí)間，跟 n 的規(guī)模無(wú)關(guān)。
• 這里我要再?gòu)?qiáng)調(diào)一下，即便這段代碼循環(huán) 10000 次、100000 次，只要是一個(gè)已知的數(shù)，跟 n 無(wú)關(guān)，照樣也是常量級(jí)的執(zhí)行時(shí)間。當(dāng) n 無(wú)限大的時(shí)候，就可以忽略。盡管對(duì)代碼的執(zhí)行時(shí)間會(huì)有很大影響，但是回到時(shí)間復(fù)雜度的概念來(lái)說(shuō)，它表示的是一個(gè)算法執(zhí)行效率與數(shù)據(jù)規(guī)模增長(zhǎng)的變化趨勢(shì)，所以不管常量的執(zhí)行時(shí)間多大，我們都可以忽略掉。因?yàn)樗旧韺?duì)增長(zhǎng)趨勢(shì)并沒(méi)有影響。
• 那第二段代碼和第三段代碼的時(shí)間復(fù)雜度是多少呢？答案是 O(n) 和 O(n^2^)，你應(yīng)該能容易就分析出來(lái)，我就不啰嗦了。

綜合這三段代碼的時(shí)間復(fù)雜度，我們?nèi)∑渲凶畲蟮牧考?jí)。所以，整段代碼的時(shí)間復(fù)雜度就為 O(n^2^)。也就是說(shuō)：總的時(shí)間復(fù)雜度就等于量級(jí)最大的那段代碼的時(shí)間復(fù)雜度。那我們將這個(gè)規(guī)律抽象成公式就是：

如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))

3. 乘法法則：嵌套代碼的復(fù)雜度等于嵌套內(nèi)外代碼復(fù)雜度的乘積

剛剛說(shuō)了一個(gè)加法原則，這里說(shuō)的乘法原則，以此類推，你也應(yīng)該能「猜到」公式。這個(gè)是效率最差的

如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))。

也就是說(shuō)，假設(shè) T1(n) = O(n)，T2(n) = O(n2)，則

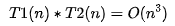
。落實(shí)到具體的代碼上，我們可以把乘法法則看成是嵌套循環(huán)。

int cal(int n) {
   int ret = 0;
   int i = 1;
   for(x=1; i <= n; x++){
       for(i = 1; i <= n; i++) {
           j = i;
           j++;
        }
 }
 }

我們單獨(dú)看 cal() 函數(shù)。假設(shè) 5-8 行的 只是一個(gè)普通的操作，那第 4 行的時(shí)間復(fù)雜度就是，T1(n) = O(n)。但 5-8 函數(shù)本身不是一個(gè)簡(jiǎn)單的操作，它的時(shí)間復(fù)雜度是 T2(n) = O(n)，所以，整個(gè) cal() 函數(shù)的時(shí)間復(fù)雜度就是，

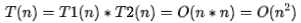
幾種常見(jiàn)時(shí)間復(fù)雜度實(shí)例

雖然代碼千差萬(wàn)別，但是常見(jiàn)的復(fù)雜度量級(jí)并不多。老弟稍微總結(jié)了一下，這些復(fù)雜度量級(jí)幾乎涵蓋了今后可以接觸的所有代碼的復(fù)雜度量級(jí)。

劃重點(diǎn)了同學(xué)們。

對(duì)于剛羅列的復(fù)雜度量級(jí)，我們可以粗略地分為兩類，多項(xiàng)式量級(jí)和非多項(xiàng)式量級(jí)。其中，非多項(xiàng)式量級(jí)只有兩個(gè)：

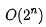
和 O(n!)。

當(dāng)數(shù)據(jù)規(guī)模 n 越來(lái)越大時(shí)，非多項(xiàng)式量級(jí)算法的執(zhí)行時(shí)間會(huì)急劇增加，求解問(wèn)題的執(zhí)行時(shí)間會(huì)無(wú)限增長(zhǎng)。所以，非多項(xiàng)式時(shí)間復(fù)雜度的算法其實(shí)是非常低效的算法。因此，關(guān)于 NP 時(shí)間復(fù)雜度我就不展開(kāi)講了。

我們主要來(lái)看幾種常見(jiàn)的多項(xiàng)式時(shí)間復(fù)雜度。

1. O(1) 之一擊必殺

首先我們必須明確一個(gè)概念，O(1) 只是常量級(jí)時(shí)間復(fù)雜度的一種表示方法，并不是指只執(zhí)行了一行代碼。比如這段代碼，即便有 3 行，它的時(shí)間復(fù)雜度也是 O(1），而不是 O(3)。

int a = 1;
int b = 2;
int c = 3;

我們的 HashMap get()、put() 其實(shí)就是 O(1) 時(shí)間復(fù)雜度。

只要代碼的執(zhí)行時(shí)間不隨 n 的增大而增長(zhǎng)，這樣代碼的時(shí)間復(fù)雜度我們都記作 O(1)。或者說(shuō)，**一般情況下，只要算法中不存在循環(huán)語(yǔ)句、遞歸語(yǔ)句，即使有成千上萬(wàn)行的代碼，其時(shí)間復(fù)雜度也是 Ο(1)**。

2. O(logn)、O(nlogn)

對(duì)數(shù)階時(shí)間復(fù)雜度非常常見(jiàn)，同時(shí)也是最難分析的一種時(shí)間復(fù)雜度。

i=1;
 while (i <= n)  {
   i = i * 2;
 }

根據(jù)我們前面講的復(fù)雜度分析方法，第三行代碼是循環(huán)執(zhí)行次數(shù)最多的。所以，我們只要能計(jì)算出這行代碼被執(zhí)行了多少次，就能知道整段代碼的時(shí)間復(fù)雜度。

從代碼中可以看出，變量 i 的值從 1 開(kāi)始取，每循環(huán)一次就乘以 2。當(dāng)大于 n 時(shí)，循環(huán)結(jié)束。還記得我們高中學(xué)過(guò)的等比數(shù)列嗎？實(shí)際上，變量 i 的取值就是一個(gè)等比數(shù)列。如果我把它一個(gè)一個(gè)列出來(lái)，就應(yīng)該是這個(gè)樣子的：

所以，我們只要知道 x 值是多少，就知道這行代碼執(zhí)行的次數(shù)了。通過(guò) 2^x^=n 求解 x 這個(gè)問(wèn)題我們想高中應(yīng)該就學(xué)過(guò)了，我就不多說(shuō)了。x=log~2~n，所以，這段代碼的時(shí)間復(fù)雜度就是 O(log~2~n)。

我把代碼稍微改下，這段代碼的時(shí)間復(fù)雜度是多少？

i=1;
 while (i <= n)  {
   i = i * 3;
 }

很簡(jiǎn)單就能看出來(lái)，這段代碼的時(shí)間復(fù)雜度為 O(log~3~n)。

實(shí)際上，不管是以 2 為底、以 3 為底，還是以 10 為底，我們可以把所有對(duì)數(shù)階的時(shí)間復(fù)雜度都記為 O(logn)。

為什么呢？

我們知道，對(duì)數(shù)之間是可以互相轉(zhuǎn)換的，log3n 就等于 log~3~2 _ log~2~n，所以 O(log~3~n) = O(C _ log~2~n)，其中 C=log~3~2 是一個(gè)常量。

基于我們前面的一個(gè)理論：**在采用大 O 標(biāo)記復(fù)雜度的時(shí)候，可以忽略系數(shù)，即 O(Cf(n)) = O(f(n))**。

所以，O(log~2~n) 就等于 O(log~3~n)。因此，在對(duì)數(shù)階時(shí)間復(fù)雜度的表示方法里，我們忽略對(duì)數(shù)的“底”，統(tǒng)一表示為 O(logn)。

如果你理解了我前面講的 O(logn)，那 O(nlogn) 就很容易理解了。

還記得我們剛講的乘法法則嗎？如果一段代碼的時(shí)間復(fù)雜度是 O(logn)，我們循環(huán)執(zhí)行 n 遍，時(shí)間復(fù)雜度就是 O(nlogn) 了。

而且，O(nlogn) 也是一種非常常見(jiàn)的算法時(shí)間復(fù)雜度。比如，歸并排序、快速排序的時(shí)間復(fù)雜度都是 O(nlogn)。

如下所示就是

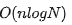
  , 內(nèi)部 while 循環(huán)是 O(logn) ,被外層 for 循環(huán)包起來(lái)。所以 就是 O(nlogn)

for(m = 1; m < n; m++) {
    i = 1;
    while(i < n) {
        i = i * 2;
    }
}

3. O(m+n)、O(m*n)

我們?cè)賮?lái)講一種跟前面都不一樣的時(shí)間復(fù)雜度，代碼的復(fù)雜度由兩個(gè)數(shù)據(jù)的規(guī)模來(lái)決定。

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

從代碼中可以看出，m 和 n 是表示兩個(gè)數(shù)據(jù)規(guī)模。我們無(wú)法事先評(píng)估 m 和 n 誰(shuí)的量級(jí)大，所以我們?cè)诒硎緩?fù)雜度的時(shí)候，就不能簡(jiǎn)單地利用加法法則，省略掉其中一個(gè)。所以，上面代碼的時(shí)間復(fù)雜度就是 O(m+n)。

針對(duì)這種情況，原來(lái)的加法法則就不正確了，我們需要將加法規(guī)則改為：T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法則繼續(xù)有效：T1(m)_T2(n) = O(f(m) _ f(n))。

**4.線性階 O(n) **

看這段代碼會(huì)執(zhí)行多少次呢？

for(i=1; i<=n; i++) {
   j = i;
   j++;
}

第 1 行會(huì)執(zhí)行 n 次，第 2 行和第 3 行會(huì)分別執(zhí)行 n 次，總的執(zhí)行時(shí)間也就是 3n + 1 次，那它的時(shí)間復(fù)雜度表示是 O(3n + 1) 嗎？No !

還是那句話：“大 O 符號(hào)表示法并不是用于來(lái)真實(shí)代表算法的執(zhí)行時(shí)間的，它是用來(lái)表示代碼執(zhí)行時(shí)間的增長(zhǎng)變化趨勢(shì)的”。

所以它的時(shí)間復(fù)雜度其實(shí)是 O(n);

平方階 O(n2)

for(x=1; i <= n; x++){
   for(i = 1; i <= n; i++) {
       j = i;
       j++;
    }
}

把 O(n) 的代碼再嵌套循環(huán)一遍，它的時(shí)間復(fù)雜度就是 O(n2) 了。

立方階 O(n3)、K 次方階 O(n^k^)

參考上面的 O(n2) 去理解就好了，O(n3)相當(dāng)于三層 n 循環(huán)，其它的類似。

空復(fù)雜度分析

理解了前面講的內(nèi)容，空間復(fù)雜度分析方法學(xué)起來(lái)就非常簡(jiǎn)單了。

時(shí)間復(fù)雜度的全稱是漸進(jìn)時(shí)間復(fù)雜度，表示算法的執(zhí)行時(shí)間與數(shù)據(jù)規(guī)模之間的增長(zhǎng)關(guān)系。類比一下，空間復(fù)雜度全稱就是漸進(jìn)空間復(fù)雜度，表示算法的存儲(chǔ)空間與數(shù)據(jù)規(guī)模之間的增長(zhǎng)關(guān)系。

void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }
}

跟時(shí)間復(fù)雜度分析一樣，我們可以看到，第 2 行代碼中，我們申請(qǐng)了一個(gè)空間存儲(chǔ)變量 i，但是它是常量階的，跟數(shù)據(jù)規(guī)模 n 沒(méi)有關(guān)系，所以我們可以忽略。

第 3 行申請(qǐng)了一個(gè)大小為 n 的 int 類型數(shù)組，除此之外，剩下的代碼都沒(méi)有占用更多的空間，所以整段代碼的空間復(fù)雜度就是 O(n)。

打個(gè)不恰當(dāng)?shù)谋扔鳎拖裎覀兊氖謾C(jī)現(xiàn)在工藝越來(lái)越好，手機(jī)也越來(lái)越薄。占用體積越來(lái)越小。也就是用更好的模具設(shè)計(jì)放置零件，而模具就像是空間復(fù)雜度更小的體積容納更多的原件。

我們常見(jiàn)的空間復(fù)雜度就是 O(1)、O(n)、O(n2 )，像 O(logn)、O(nlogn) 這樣的對(duì)數(shù)階復(fù)雜度平時(shí)都用不到。而且，空間復(fù)雜度分析比時(shí)間復(fù)雜度分析要簡(jiǎn)單很多。所以，對(duì)于空間復(fù)雜度，掌握剛我說(shuō)的這些內(nèi)容已經(jīng)足夠了。

空間復(fù)雜度 O(1)

如果算法執(zhí)行所需要的臨時(shí)空間不隨著某個(gè)變量 n 的大小而變化，即此算法空間復(fù)雜度為一個(gè)常量，可表示為 O(1)。

int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

代碼中的 i、j、m 所分配的空間都不隨著處理數(shù)據(jù)量變化，因此它的空間復(fù)雜度 S(n) = O(1)。

空間復(fù)雜度 O(n)

int[] m = new int[n]
for(i=1; i <= n; ++i) {
   j = i;
   j++;
}

這段代碼中，第一行 new 了一個(gè)數(shù)組出來(lái)，這個(gè)數(shù)據(jù)占用的大小為 n，后面雖然有循環(huán)，但沒(méi)有再分配新的空間，因此，這段代碼的空間復(fù)雜度主要看第一行即可，即 S(n) = O(n)。

總結(jié)

基礎(chǔ)復(fù)雜度分析的知識(shí)到此就講完了，我們來(lái)總結(jié)一下。

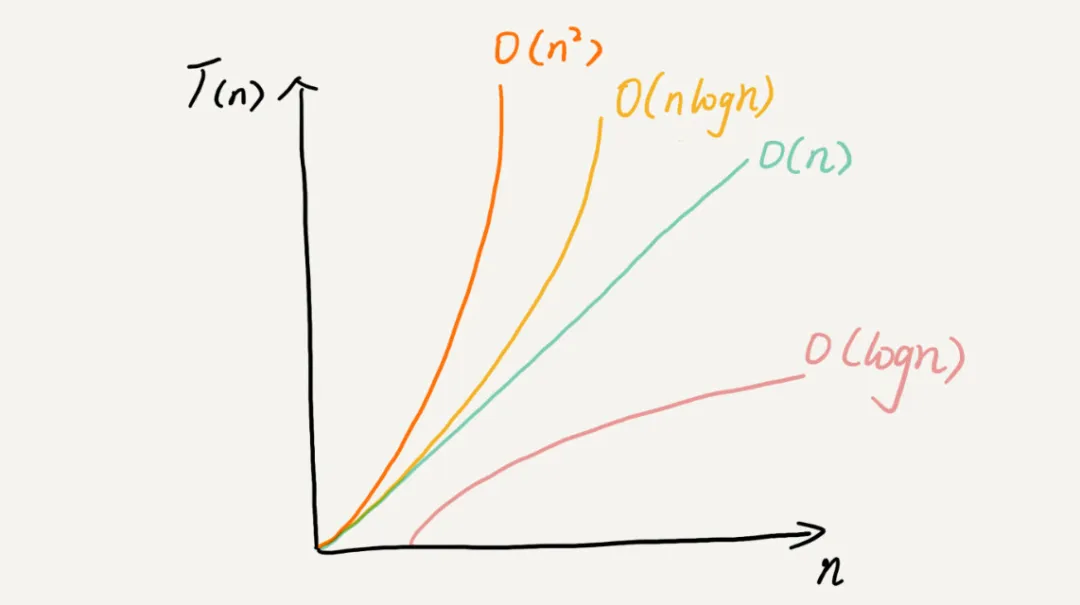
復(fù)雜度也叫漸進(jìn)復(fù)雜度，包括時(shí)間復(fù)雜度和空間復(fù)雜度，用來(lái)分析算法執(zhí)行效率與數(shù)據(jù)規(guī)模之間的增長(zhǎng)關(guān)系，可以粗略地表示，越高階復(fù)雜度的算法，執(zhí)行效率越低。

常見(jiàn)的復(fù)雜度并不多，從低階到高階有：O(1)、O(logn)、O(n)、O(nlogn)、O(n^2^ )。等學(xué)完整個(gè)專欄之后，就會(huì)發(fā)現(xiàn)幾乎所有的數(shù)據(jù)結(jié)構(gòu)和算法的復(fù)雜度都跑不出這幾個(gè)。

有人說(shuō)，我們項(xiàng)目之前都會(huì)進(jìn)行性能測(cè)試，再做代碼的時(shí)間復(fù)雜度、空間復(fù)雜度分析，是不是多此一舉呢？而且，每段代碼都分析一下時(shí)間復(fù)雜度、空間復(fù)雜度，是不是很浪費(fèi)時(shí)間呢？你怎么看待這個(gè)問(wèn)題呢？