KAN干翻MLP,開創(chuàng)神經(jīng)網(wǎng)絡新范式!一個數(shù)十年前數(shù)學定理,竟被MIT華人學者復活了
KAN的橫空出世,徹底改變了神經(jīng)網(wǎng)絡研究范式!
神經(jīng)網(wǎng)絡是目前AI領域最強大的工具。當我們將其擴展到更大的數(shù)據(jù)集時,沒有什么能夠與之競爭。
圓周理論物理研究所研究員Sebastian Wetzel,對神經(jīng)網(wǎng)絡給予了高度的評價。

然而,萬事萬物并非「絕對存在」,神經(jīng)網(wǎng)絡一直有一個劣勢。
其中一個基本組件——多層感知器(MLP),盡管立了大功,但這些建立在MLP之上的神經(jīng)網(wǎng)絡,卻成為了「黑盒」。
因為,人們根本無法解釋,其中運作的原理。

為此,AI界的研究人員們一直在想,是否存在不同類型的神經(jīng)網(wǎng)絡,能夠以更透明的方式,同樣輸出可靠的結(jié)果?
是的,的確存在。
2024年4月,MIT、加州理工等機構研究人員聯(lián)手提出,新一代神經(jīng)網(wǎng)絡架構——Kolmogorov-Arnold network(KAN)。
它的出現(xiàn),解決了以上的「黑盒」問題。

論文地址:https://arxiv.org/pdf/2404.19756
比起MLP,KAN架構更加透明,而且?guī)缀蹩梢酝瓿善胀ㄉ窠?jīng)網(wǎng)絡,在處理某類問題時的所有工作。
值得一提的是,它的誕生源于上個世紀中期一個數(shù)學思想。

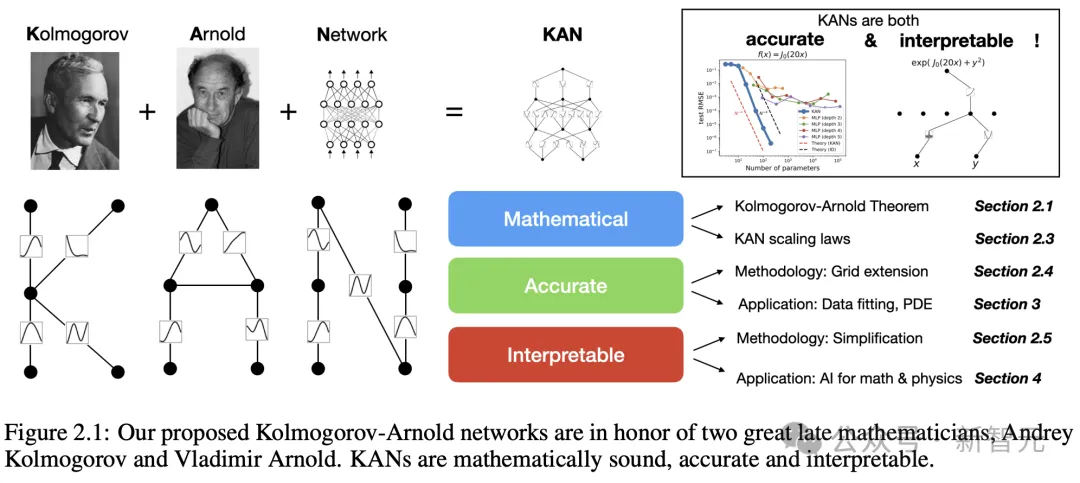
數(shù)學家Andrey Kolmogorov和Vladimir Arnold
這個已經(jīng)埋了30多年的數(shù)學原理,如今在DL時代被這位華人科學家和團隊重新發(fā)現(xiàn),再次發(fā)光發(fā)亮。

雖然,這項創(chuàng)新僅僅誕生了5個月的時間,但KAN已經(jīng)在研究和編碼社區(qū),掀起了巨浪。
約翰霍普金斯大學計算機教授Alan Yuille贊揚道,KAN更易于解釋,可以從數(shù)據(jù)中提取科學規(guī)則,因此在科學領域中有著極大的應用」。
讓不可能,成為可能
典型的神經(jīng)網(wǎng)絡工作原理是這樣的:
一層層人工神經(jīng)元/節(jié)點,通過人工突觸/邊,進行連接。信息經(jīng)過每一層,經(jīng)過處理后再傳輸?shù)较乱粚樱钡阶罱K將其輸出。
對邊進行加權,權重較大的邊,比其他邊有更大的影響。
在所謂的訓練期間,這些權重會不斷調(diào)整,最終使得神經(jīng)網(wǎng)絡輸出越來越接近正確答案。
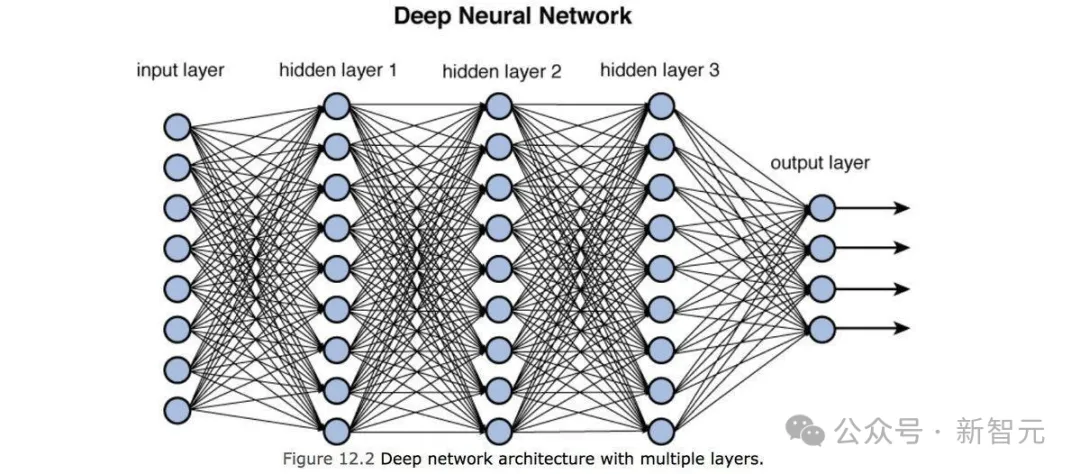
神經(jīng)網(wǎng)絡的一個常見的目標是,找到一種數(shù)學函數(shù)、曲線,以便最好地連接某些數(shù)據(jù)點。
它們越接近這個函數(shù),預測的結(jié)果就越準確。
假設神經(jīng)網(wǎng)絡模擬了物理過程,理想情況下,輸出函數(shù)將代表描述該物理過程的方程,相當于物理定律。
對于MLP來說,會有一個數(shù)學定理,告訴你神經(jīng)網(wǎng)絡能多接近最佳可能函數(shù)。
這個定理表明,MLP無法完美地表示這個函數(shù)。
不過,在恰當?shù)那闆r下,KAN卻可以做到。
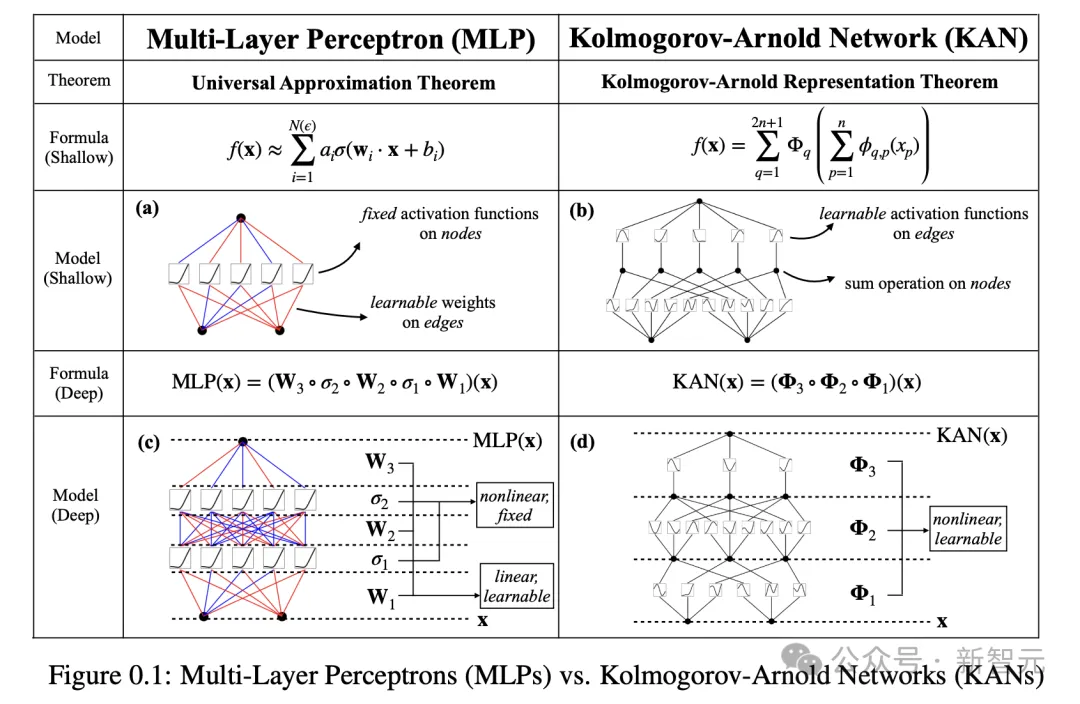
KAN以一種不同于MLP的方式,進行函數(shù)擬合,將神經(jīng)網(wǎng)絡輸出的點連接起來。
它不依賴于帶有數(shù)值權重的邊,而是使用函數(shù)。
同時,KAN的邊函數(shù)是非線性和可學習的,這使得它們比MLP更靈活、敏感。
然而,在過去的35年里,KAN被認為在實際應用中,切不可行。
1989年,由MIT物理學家轉(zhuǎn)計算機神經(jīng)科學家Tomaso Poggio,共同撰寫的一篇論文中明確指出:
KAN核心的數(shù)學思想,在學習神經(jīng)網(wǎng)絡的背景下是無關緊要的。
Poggio的一個擔憂,可以追溯到KAN核心的數(shù)學概念。

論文地址:http://cbcl.mit.edu/people/poggio/journals/girosi-poggio-NeuralComputation-1989.pdf
1957年,數(shù)學家Andrey Kolmogorov和Vladimir Arnold在各自但相互補充的論文中證明——如果你有一個使用多個變量的單一數(shù)學函數(shù),你可以把它轉(zhuǎn)換成多個函數(shù)的組合,每個函數(shù)都有一個變量。

然而,這里有個一個重要的問題。
這個定理產(chǎn)生的單個變量函數(shù),可能是「不平滑的」,意味著它們可能產(chǎn)生尖銳的邊緣,就像V字的頂點。
這對于任何試圖使用這個定理,重建多變量函數(shù)的神經(jīng)網(wǎng)絡來說,都是一個問題所在。
因為這些更簡單的單變量部分,需要是平滑的,這樣它們才能在訓練過程中,學會正確地調(diào)增匹配目標值。
因此,KAN的前景一直以來黯淡無光。
MIT華人科學家,重新發(fā)現(xiàn)KAN
直到去年1月,MIT物理學研究生Ziming Liu,決定重新探討這個話題。
他和導師Max Tegmark,一直致力于讓神經(jīng)網(wǎng)絡在科學應用中,更加容易被人理解,能夠讓人們窺探到黑匣子的內(nèi)部。
然而,這件事一直遲遲未取得進展。

可以說,在這種「走投無路」的情況下,Liu決定在KAN上孤勇一試。
導師卻在這時,潑了一盆冷水,因為他對Poggio論文觀點太過熟悉,并堅持認為這一努力會是一個死胡同。
不過,Ziming Liu卻沒有被嚇到,他不想在沒有先試一下的情況下,放棄這個想法。
隨后,Tegmark也慢慢改變了自己的想法。
他們突然認識到,即使由該定理產(chǎn)生的單值函數(shù),是不平滑的,但神經(jīng)網(wǎng)絡仍可以用平滑的函數(shù)逼近數(shù)值。
Liu似乎有一種直覺,認定了KAN便是那個拯救者。
因為自Poggio發(fā)表論文,已經(jīng)過了35年,當下的軟件和硬件取得了巨大的進步。
在2024年,就計算來講,讓許多事情成為可能。
大約肝了一周左右的時間,Liu深入研究了這一想法。在此期間,他開發(fā)了一些原型KAN系統(tǒng),所有系統(tǒng)都有兩層。
因為Kolmogorov-Arnold定理本質(zhì)上為這種結(jié)構提供了藍圖。這一定理,明確地將多變量函數(shù)分解為,不同的內(nèi)部函數(shù)和外部函數(shù)集。
這樣的排列,使其本身就具備內(nèi)層和外層神經(jīng)元的兩層架構。
但令Liu沮喪的是,所設計的原型KAN并沒有在科學相關任務上,表現(xiàn)地更好。
導師Tegmark隨后提出了一個關鍵的建議:為什么不嘗試兩層以上的KAN架構,或許能夠處理更加復雜的任務?
一語點醒夢中人。
這個開創(chuàng)性的想法,便成為他們突破的關鍵點。
這個羽翼未豐的原型架構,為他們帶來了希望。很快,他們便聯(lián)系了MIT、加州理工、東北大學的同事,希望團隊能有數(shù)學家,并計劃讓KAN分析的領域的專家。
實踐證明,在4月份論文中,小組團證明了三層KAN,確實是可行的。
他們給出了一個示例,三層KAN可以準確地表示一個函數(shù),而兩層KAN卻不能。
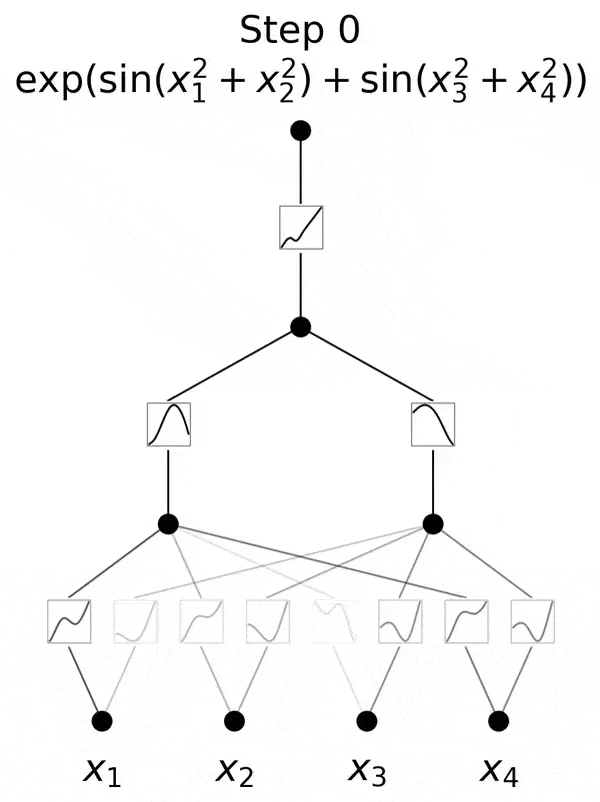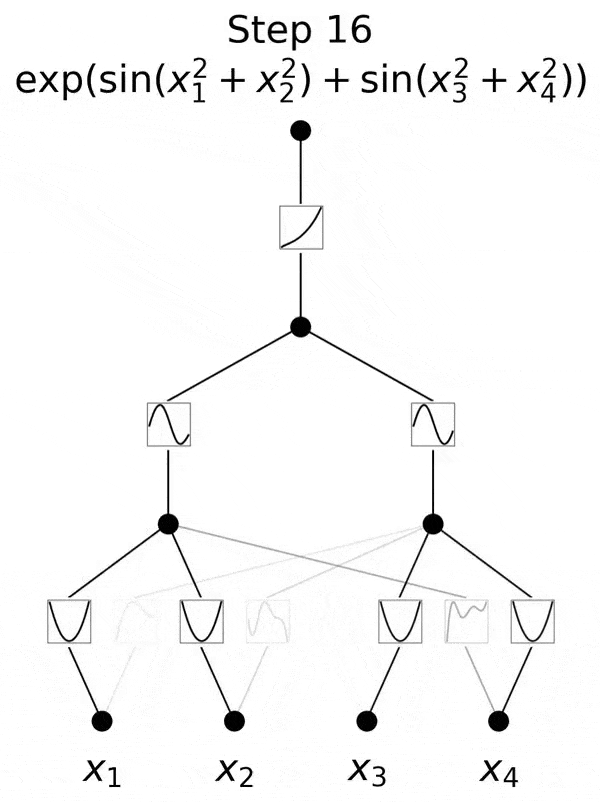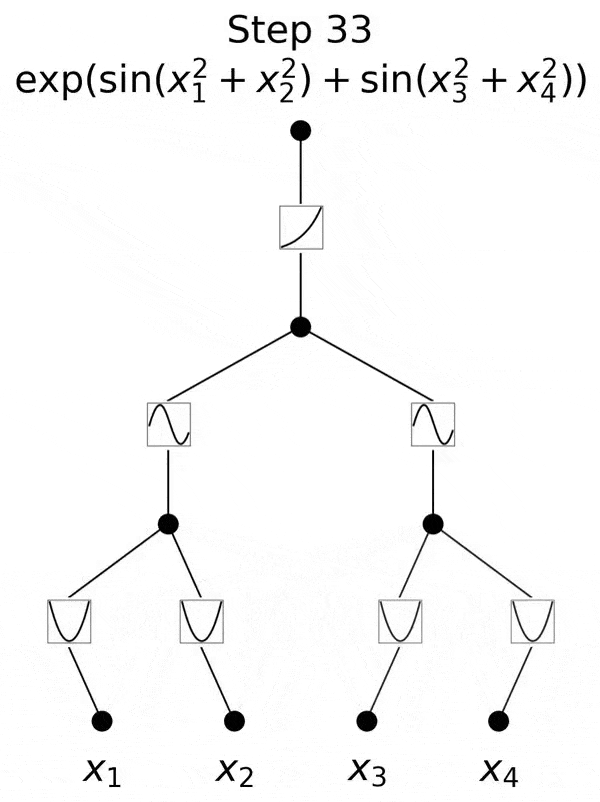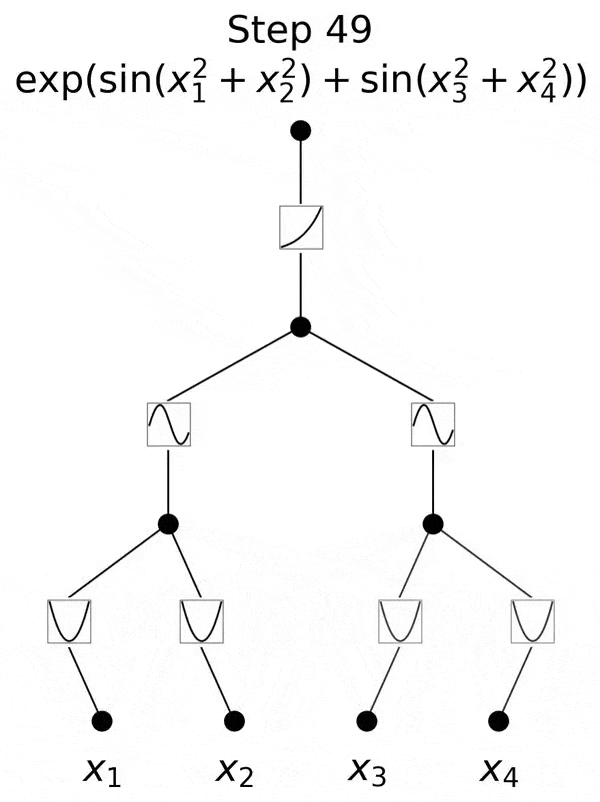
不過,研究團隊并沒有止步于此。自那以后,他們在多達六層的KAN上進行了實驗,每一層,神經(jīng)網(wǎng)絡都能與更復雜的輸出函數(shù),實現(xiàn)對準。
論文合著作者之一 Yixuan Wang表示,「我們發(fā)現(xiàn),本質(zhì)上,可以隨心所欲堆疊任意多的層」。
發(fā)現(xiàn)數(shù)學定理碾壓DeepMind
更令人震驚的是,研究者在兩個現(xiàn)實的世界問題中,對KAN完成了驗證。
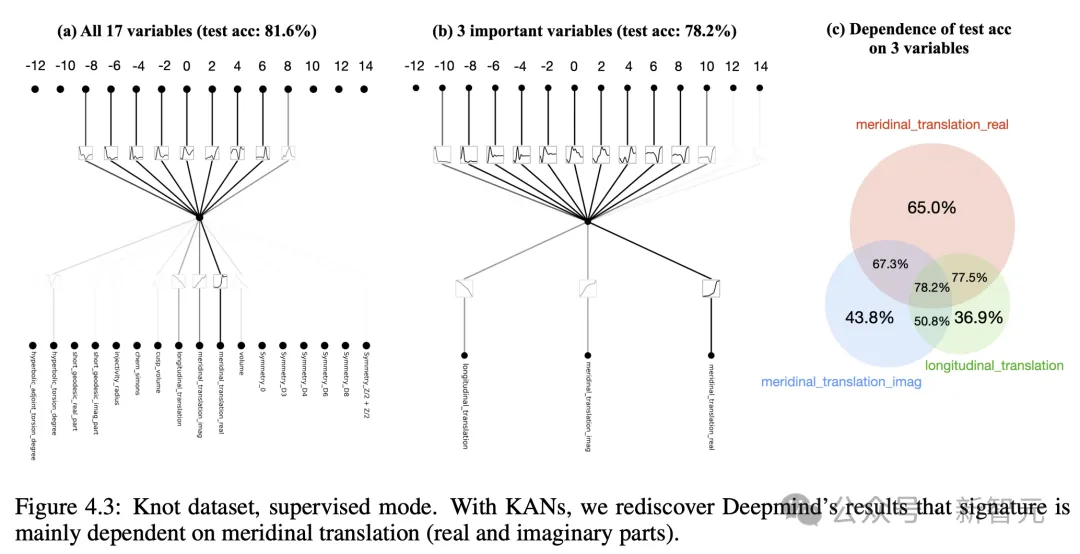
第一個,是數(shù)學一個分支中的「紐結(jié)理論」。
2021年,DeepMind團隊曾宣布,他們已經(jīng)搭建了一個MLP,再獲得足夠紐結(jié)的其他屬性后,可以預測出給定紐結(jié)的特定拓撲屬性。
三年后,全新的KAN再次實現(xiàn)了這一壯舉。
而且,它更進一步地呈現(xiàn)了,預測的屬性如何與其他屬性相關聯(lián)。
論文一作Liu說,「這是MLP根本做不到的」。
第二個問題是,設計凝聚態(tài)物理中的一種現(xiàn)象,稱為Anderson局域化。
其目的是,預測特定相變將發(fā)生的邊界,然后確定描述該過程的數(shù)學公式。同樣,也只有KAN做到了在這一點。
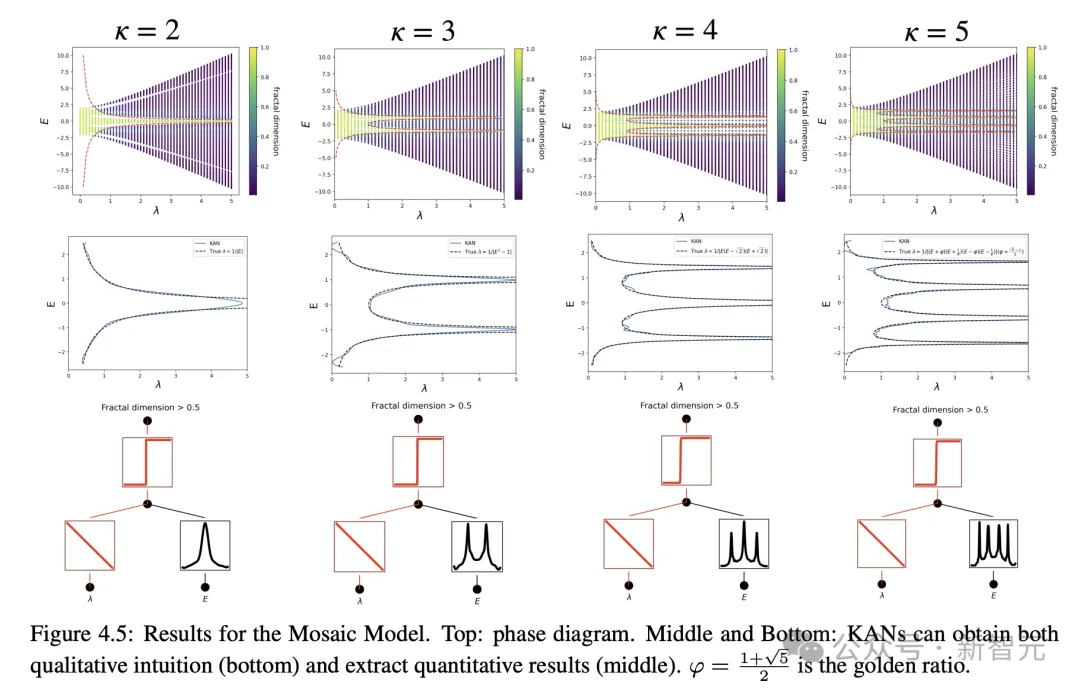
Tegmark表示,「但與其他形式的神經(jīng)網(wǎng)絡相比,KAN的最大優(yōu)勢在于其可解釋性,這也是KAN近期發(fā)展的主要動力」。
在以上的兩個例子中,KAN不僅給出了答案,還提供了解釋。
他還問道,可解釋性意味著什么?
「如果你給我一些數(shù)據(jù),我會給你一個可以寫在T恤上的公式」。
終極方程式?
KAN這篇論文的出世,在整個AI圈引起了轟動。
AI大佬們紛紛給予了高度的評價,有人甚至直呼,機器學習的新紀元開始了!

目前,這篇論文在短短三個月的時間里,被引次數(shù)近100次。
很快,其他研究人員親自入局,開始研究自己的KAN。
6月,清華大學等團隊的研究人員發(fā)表了一篇論文稱,他們的 Kolmogorov-Arnold-informed neural network(KINN),在求解偏微方程(PDE)方面,明顯優(yōu)于MLP。
對于研究人員來說,這可不是一件小事,因為PED在科學中的應用無處不在。
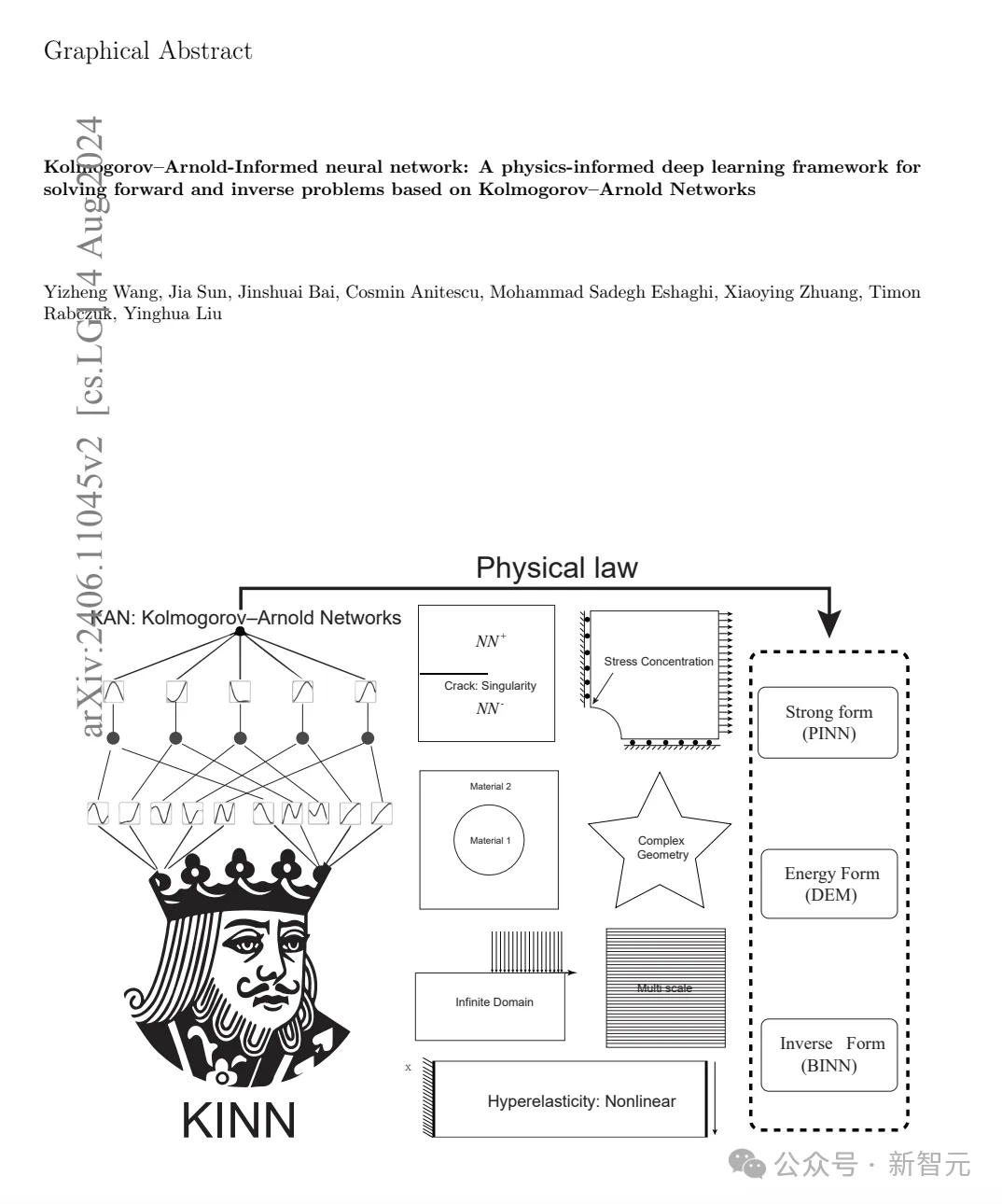
論文地址:https://arxiv.org/pdf/2406.11045
緊接著,7月,來自新加坡國立大學的研究人員們,對KAN和MLP架構做了一個全面的分析。
他們得出結(jié)論,在可解釋性的相關任務中,KAN的表現(xiàn)優(yōu)于MLP,同時,他們還發(fā)現(xiàn)MLP在計算機視覺和音頻處理方面做的更好。
而且,這兩個網(wǎng)絡架構在NLP,以及其他ML任務上,性能大致相當。
這一結(jié)果在人意料之中,因為KAN團隊的重點一直是——科學相關的任務,而且,在這些任務中,可解釋性是首要的。

論文地址:https://arxiv.org/pdf/2407.16674
與此同時,為了讓KAN更加實用、更容易使用。

8月,KAN原班人馬團隊再次迭代了架構,發(fā)表了一篇名為「KAN 2.0」新論文。

論文地址:https://arxiv.org/pdf/2408.10205
他們將其描述為,它更像是一本用戶手冊,而非一篇傳統(tǒng)的論文。
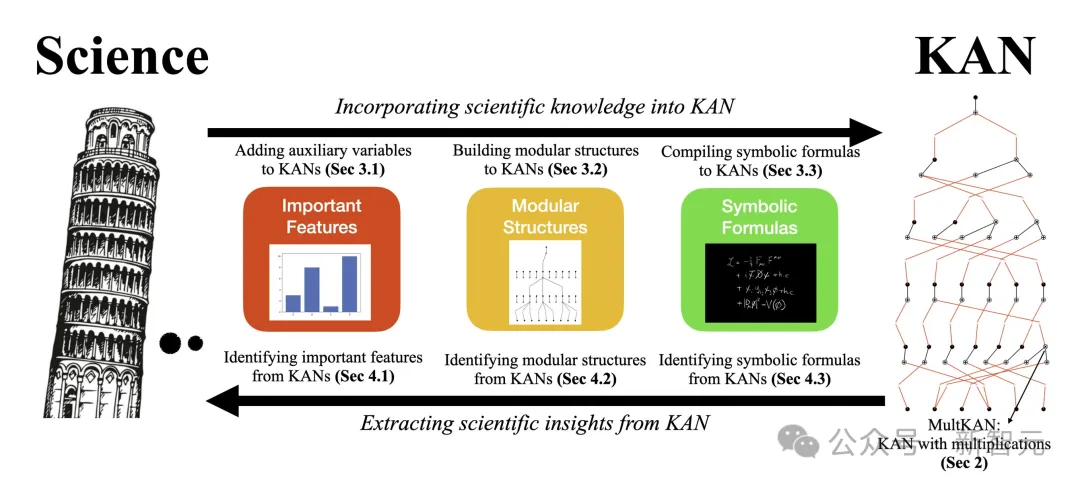
論文合著者認為,KAN不僅僅是一種達到目的的手段,更是一種全新的科學研究方法。
長期以來,「應用驅(qū)動的科學」在機器學習領域占據(jù)主導地位,KAN的誕生促進了所謂的「好奇心驅(qū)動的科學」的發(fā)展。
比如,在觀察天體運動時,應用驅(qū)動型研究人員,專注于預測它們的未來狀態(tài),而好奇心驅(qū)動型研究人員,則希望揭示運行背后的物理原理。

Liu希望,通過KAN,研究人員可以從中獲得更多,而不僅僅是在其他令人生畏的計算問題上尋求幫助。
相反,他們可能會把重點放在,僅僅是為了理解,而獲得理解之上。