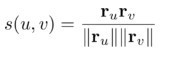推薦系統(tǒng)中的 Scaling Law : 看特征維度如何影響推薦系統(tǒng)準確性
譯文譯者 | 汪昊
審校 | 重樓
推薦系統(tǒng)在互聯(lián)網(wǎng)行業(yè)應用廣泛。根據(jù)亞馬遜和Netflix 等公司的經(jīng)驗,推薦系統(tǒng)可以給公司帶來大幅度的流量提升,從而起到開源節(jié)流的作用。試想如果不借助于推薦系統(tǒng),而是借助于搜索引擎關鍵詞進行引流,那么營銷的花費將增加數(shù)倍乃至數(shù)百倍都有可能。因此,大型互聯(lián)網(wǎng)公司對于推薦系統(tǒng)不管怎么重視都不為過。

業(yè)界對于推薦系統(tǒng)的研究,主要集中在如何提升推薦系統(tǒng)的準確率方面。隨著近年來大模型的火熱,在信息檢索頂會上,曾經(jīng)出現(xiàn)研究大模型 Scaling Law 的文章獲得最佳論文獎的情況。而推薦系統(tǒng)領域在 2023 年也出現(xiàn)了一篇類似的文章,講的是推薦系統(tǒng)矩陣分解模型中特征向量的維度的大小對于準確率的影響。這篇論文題目是 Curse of Low Dimensionality in Recommender System,發(fā)表在信息檢索領域頂會SIGIR 2023 上。下面我們來一探這篇論文的究竟。
作者首先給出了推薦系統(tǒng)點乘模型的一般公式:
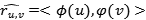
其中
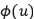
是用戶側的嵌入式向量,而
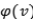
是物品側的嵌入式向量。推薦系統(tǒng)點乘模型的一個典型例子是 Alternating Least Squares (ALS)。這個算法被集成在了 Apache Spark 的 MLLib 算法庫里。作者在本文中將在 MovieLens 20M,Million Song Dataset 和 Epinions 數(shù)據(jù)集上測試 ALS 算法,以考察嵌入式向量的維度對于推薦系統(tǒng)準確率的影響。
作者通過對比實驗檢驗流行度偏差,得到了下圖:
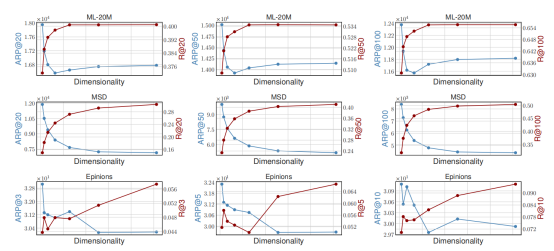
隨后,作者檢驗了算法的召回率,得到了下圖:
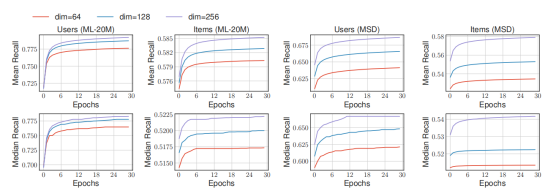
作者通過實驗觀察得到結論,高維度的嵌入式表達可以得到更高的準確度和更低的流行度偏差。
作者隨后對于嵌入式表達進行了理論建模,得到了以下定理:
定理 4.1 以下結論成立:
- 上界:對于每一組在空間的 n 個物品向量來說,能利用這些向量表示的長度為 K 的排序列表數(shù)量至多數(shù) 。
- 下界: 存在一組在空間的物品向量,這組向量的數(shù)量是 n,能利用這組向量來表示的長度為 d 的排序列表數(shù) 。
以上定理表明增加嵌入式向量維度,會指數(shù)級別的增強點乘模型的表達能力。
為了研究流行度偏差背后的機理,作者隨后又提出了如下定理:
定理 4.2 假定存在兩個物品集合 P 和 L,查詢向量 q 在點乘模型中總是將 P 集合中的物品排名優(yōu)于所有的L 集合中的物品。那么,如果一個向量 s 被包括在一個凸錐中,而這個凸錐又包含了 P 的凸包,那么 s 比 L 中的每一個物品排名都高。另外,這個凸錐會隨著更多物品的加入而變得更大。
這個定理告訴我們因為存在一小撮流形和長尾的物品,它們使得比較流形的物品排名優(yōu)于長尾物品,降低了可表達的排序列表的數(shù)量,因此我們無法完全避免流行度偏差。
在本文中,作者根據(jù)實驗和后續(xù)的理論分析指出低維嵌入式向量會導致關于流行度偏差的過擬合,并會進一步加深流行度偏差的問題。這一現(xiàn)象,被稱為低維度詛咒。作者的研究工作條理分明,除了大量的實驗對比工作,還進行了嚴謹?shù)睦碚摲治觯虼酥档猛扑]系統(tǒng)行業(yè)的從業(yè)者認真學習。
譯者簡介
汪昊,前達評奇智董事長兼創(chuàng)始人。前 FunPlus 人工智能實驗室負責人。在 ThoughtWorks, 百度,聯(lián)想,網(wǎng)易和 FunPlus 等科技公司有超過 13 年的技術和技術管理經(jīng)驗。精通推薦系統(tǒng)、金融風控、爬蟲和聊天機器人等領域。在國際學術會議和期刊發(fā)表論文 44 篇。5 次獲得國際學術會議最佳論文獎和最佳論文報告獎。2006 年 ACM/ICPC 北美落基山區(qū)域賽金牌。2004 年全國大學生英語能力競賽口語總決賽銅牌。本科(2008年)和碩士(2010年)畢業(yè)于美國猶他大學。對外經(jīng)貿(mào)大學(2016 年)在職 MBA 學位。