在過去幾年里，大語言模型（LLM）與深度學習的浪潮席卷了幾乎所有計算領域。從醫(yī)學診斷到金融建模，從化學分子設計到物理模擬，這些模型在推理任務上的表現(xiàn)一次次刷新了人們的認知。

它們不僅能處理復雜的自然語言，還能跨越模態(tài)邊界，將圖像、語音、代碼等信息融會貫通，展現(xiàn)出驚人的“多才多藝”。

然而在這股熱潮背后，一個更為基礎的問題卻始終懸而未決——我們究竟能否量化并刻畫人工智能推理能力的極限？

當前的理論體系對這一問題的回答并不充分。雖然我們知道神經(jīng)網(wǎng)絡在足夠的訓練和數(shù)據(jù)條件下具有極強的表達能力，但這種“能力”究竟能延伸到哪些推理類型、能否覆蓋所有可計算的算法、在復雜度上又有何代價，這些問題依然缺乏系統(tǒng)的數(shù)學刻畫。

換句話說，我們對“AI推理的邊界”缺乏一個可驗證、可量化的理論框架。

近日，arXiv 熱文《Quantifying The Limits of AI Reasoning:Systematic Neural Network Representations of Algorithms》直面了一個核心問題：在理想化的訓練條件下（無限完美數(shù)據(jù)與完美優(yōu)化），神經(jīng)網(wǎng)絡究竟能執(zhí)行哪些類型的推理任務？

現(xiàn)有的通用逼近定理雖然證明了神經(jīng)網(wǎng)絡可以逼近任意連續(xù)函數(shù)，但它們往往將函數(shù)視為“黑箱”映射，忽略了函數(shù)背后的算法結(jié)構(gòu)與推理鏈條。這種忽視意味著，我們無法從逼近理論中直接推導出網(wǎng)絡在執(zhí)行具體推理任務時的復雜度與可行性。

研究目標是通過引入電路復雜度的視角，將推理任務視為電路計算過程，并建立一種系統(tǒng)化的方法，將任意電路精確映射為ReLU前饋神經(jīng)網(wǎng)絡。

這不僅能量化網(wǎng)絡的推理能力，還能揭示網(wǎng)絡規(guī)模與算法運行時間之間的關系，從而為“AI推理極限”提供一個可計算的度量標準。

研究團隊來自加拿大麥克馬斯特大學數(shù)學與統(tǒng)計系，并與向量人工智能研究院（Vector Institute）緊密合作。團隊成員在數(shù)學邏輯、計算復雜度、神經(jīng)網(wǎng)絡理論等領域都有深厚積累，既具備嚴謹?shù)睦碚摴Φ祝质煜I前沿應用的需求。

這種跨學科背景，使他們能夠在抽象的數(shù)學框架與具體的AI推理任務之間架起橋梁。

1.相關研究與理論基礎

要理解這項工作的意義，必須先回顧通用逼近定理的歷史與局限。上世紀80年代末，Hornik、Cybenko、Funahashi等人的經(jīng)典結(jié)果證明，具有足夠隱藏單元的前饋神經(jīng)網(wǎng)絡可以在任意精度下逼近任意連續(xù)函數(shù)。

這一發(fā)現(xiàn)奠定了神經(jīng)網(wǎng)絡表達能力的理論基礎，也為深度學習的興起提供了信心。然而，這類定理關注的是“函數(shù)映射”層面的能力——它們并不關心函數(shù)是如何被計算出來的，更不涉及計算過程的結(jié)構(gòu)與復雜度。

圖1：比較：經(jīng)典近似理論與我們的復雜性理論改進。

相比之下，電路復雜度理論則從另一個角度刻畫計算能力。它將算法視為由基本運算單元（門）組成的電路，研究在給定門集下實現(xiàn)某個函數(shù)所需的最小電路規(guī)模與深度。

不同類型的電路——布爾電路（處理邏輯運算）、算術電路（處理加法與乘法）、熱帶電路（處理最小值與加法）——對應著不同類別的推理任務。

在形式化表示上，這些電路的計算過程可以抽象為有向無環(huán)圖（DAG）。DAG的節(jié)點代表計算步驟，邊表示數(shù)據(jù)流動。輸入節(jié)點接收原始數(shù)據(jù)，計算節(jié)點執(zhí)行基本運算，輸出節(jié)點給出最終結(jié)果。

這種結(jié)構(gòu)化表示不僅揭示了算法的執(zhí)行順序，也為分析推理鏈條提供了天然的工具。

有趣的是，這種“推理鏈”與大語言模型中的Chain-of-Thought（CoT）概念高度契合。

LLM在多步推理時，會生成一系列中間推斷步驟，逐步逼近最終答案；而在電路模型中，這些中間步驟正對應著DAG中的計算節(jié)點。由此，LLM的推理鏈可以被視為一種特殊的電路執(zhí)行過程，這為將AI推理能力映射到電路復雜度框架中提供了理論基礎。

圖片

圖2：主要結(jié)果總結(jié)：給定可計算函數(shù)作為電路的任何（近似）表示，我們用一個基本的ReLU神經(jīng)網(wǎng)絡（從預先指定的字典中選擇）替換每個計算節(jié)點，該網(wǎng)絡模擬相應的計算。

通過將通用逼近理論與電路復雜度結(jié)合，研究團隊為我們提供了一個新的視角：不再僅僅問“神經(jīng)網(wǎng)絡能否逼近某個函數(shù)”，而是問“神經(jīng)網(wǎng)絡能否高效地模擬計算該函數(shù)的算法過程”。這正是量化AI推理極限的關鍵所在。

2.研究方法與核心構(gòu)造

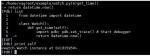
這項研究的核心，是一套研究團隊稱之為“系統(tǒng)化元算法（Meta-Algorithm）”的構(gòu)造方法。它的野心很大——無論你手里拿的是布爾電路、算術電路、熱帶電路，還是混合邏輯與算術的復雜計算圖，這個方法都能將它一步步“翻譯”成一個等價的 ReLU 前饋神經(jīng)網(wǎng)絡，而且是精確模擬，不是近似。

實現(xiàn)的思路很直觀，先把算法抽象成一個有向無環(huán)圖（DAG），每個節(jié)點就是一個“門”（gate），執(zhí)行某種基本運算。然后針對每種門類型，事先準備一個標準化的 ReLU MLP模塊作為“模擬器”。

接下來，通過一種被研究團隊形象地稱為“電路手術（Circuit Surgery）”的操作，把原電路中的節(jié)點逐一替換成對應的 MLP 模塊，并重新接好輸入輸出的連線。這樣，原電路的計算流程就被無縫嵌入到神經(jīng)網(wǎng)絡的計算圖中。

這種“手術”有幾個關鍵要求：替換后的網(wǎng)絡必須保持原有的計算依賴關系（Graph Structure Preservation），也就是說，網(wǎng)絡的拓撲結(jié)構(gòu)要和原電路的 DAG 一一對應。

同時，網(wǎng)絡的規(guī)模——也就是神經(jīng)元和參數(shù)的數(shù)量——要和原電路的復雜度成比例（Complexity Mapping），實現(xiàn)空間復雜度與時間復雜度的直接映射。

為了讓這種映射在真實計算機上成立，研究團隊還引入了數(shù)字計算模型的細節(jié)。現(xiàn)實中的計算不是在連續(xù)實數(shù)域上進行的，而是在有限精度的數(shù)值網(wǎng)格上運算。

技術論文中明確了模運算（modular arithmetic）和舍入機制（rounding scheme）的定義，并提出了“機器精度下的函數(shù)等價性”——如果兩個函數(shù)在給定精度的數(shù)值網(wǎng)格上輸出完全一致，就認為它們是等價的。這為后續(xù)的精確模擬提供了嚴格的判據(jù)。

3.主要理論結(jié)果

Theorem 1：通用推理（Universal Reasoning） 

這是全文的基石性結(jié)論。

它斷言任意由特定門集 GG 構(gòu)成的電路，都可以通過完全無缺陷的“電路手術”轉(zhuǎn)化為一個 ReLU 前饋網(wǎng)絡，并且在數(shù)字計算機上精確復現(xiàn)原電路的功能。

更重要的是，這個網(wǎng)絡的空間復雜度（神經(jīng)元數(shù)量）與原電路的時間復雜度（門數(shù)量）同階，計算圖的形狀也與原電路一致。這意味著，神經(jīng)網(wǎng)絡不僅能“算對”，還能“按原算法的節(jié)奏去算”，真正實現(xiàn)了推理過程的結(jié)構(gòu)化保真。

Theorem 2：有限精度下的通用電路設計 

如果說 Theorem 1 解決了“能不能模擬”的問題，Theorem 2 則進一步回答了“有沒有遺漏”的疑問。

它證明在有限精度的數(shù)值空間上，任何函數(shù)都可以由一個 ReLU MLP 精確實現(xiàn)。

這是一個數(shù)字計算版本的“超位定理”，與Kolmogorov–Arnold 超位定理在思想上相呼應——后者說任何多元連續(xù)函數(shù)都可以由單變量函數(shù)的疊加表示，這里則說任何有限精度函數(shù)都可以由一個通用編碼器網(wǎng)絡加上線性解碼實現(xiàn)。

與經(jīng)典的通用逼近定理相比，這兩個結(jié)果的覆蓋面更廣。通用逼近定理只能保證在無限精度、連續(xù)域上的近似，而這里的構(gòu)造不僅涵蓋了逼近，還涵蓋了推理任務的精確執(zhí)行，包括邏輯運算、動態(tài)規(guī)劃、甚至有限步的圖靈機模擬。

換句話說，它不僅回答了“神經(jīng)網(wǎng)絡能否學會某個函數(shù)”，還回答了“神經(jīng)網(wǎng)絡能否原封不動地執(zhí)行某個算法”。

圖片

圖3：定理2中構(gòu)造的最壞情況近似值的說明。

這種從電路到網(wǎng)絡的系統(tǒng)化映射，讓“AI 推理能力”第一次有了可計算、可驗證的數(shù)學刻畫，也為未來在復雜推理任務中設計高效、可解釋的神經(jīng)網(wǎng)絡架構(gòu)提供了堅實的理論支撐。

4.應用案例分析

在理論框架奠定之后，研究團隊用一系列推論（Corollary）展示了這一方法在不同類型推理任務中的威力。這些案例不僅是數(shù)學上的“存在性證明”，更是對神經(jīng)網(wǎng)絡推理邊界的一次次沖擊。

布爾函數(shù)實現(xiàn)復雜度優(yōu)化（Corollary 1） 

傳統(tǒng)上，某些布爾函數(shù)的神經(jīng)網(wǎng)絡實現(xiàn)復雜度會呈現(xiàn)雙指數(shù)級增長，這幾乎讓直接模擬變得不可行。

研究團隊通過系統(tǒng)化元算法，將這種復雜度壓縮到單指數(shù)級，逼近已知的理論下界。這意味著，在可計算性邊界附近，ReLU 網(wǎng)絡的表達效率被顯著提升，尤其是在需要精確邏輯推理的任務中。

隨機化邏輯電路去隨機化（Corollary 2） 

在經(jīng)典計算理論中，隨機化布爾電路常被用來簡化某些問題的實現(xiàn)。但研究團隊證明，這些電路可以被等價的確定性 ReLU 網(wǎng)絡替代，且不損失功能。

這不僅是一次“去隨機化”的勝利，也為構(gòu)建可驗證、可審計的推理網(wǎng)絡提供了路徑——畢竟，確定性意味著可重復性和可追溯性。

有限時間圖靈機模擬（Corollary 3） 

更具沖擊力的是，研究團隊展示了如何用 ReLU 網(wǎng)絡精確模擬有限步運行的圖靈機，并保留顯式的推理鏈。

這種模擬不是黑箱式的，而是結(jié)構(gòu)上對應原圖靈機的狀態(tài)轉(zhuǎn)移與符號操作，讓網(wǎng)絡的每一步計算都能被解釋為具體的算法步驟。

動態(tài)規(guī)劃與圖計算（Corollary 4） 

在圖計算領域，研究團隊以全點對最短路徑（All-Pairs Shortest Path, ASP）問題為例，構(gòu)造了一個立方復雜度的 ReLU 網(wǎng)絡實現(xiàn)。

這種實現(xiàn)不僅保留了動態(tài)規(guī)劃的遞推結(jié)構(gòu)，還在網(wǎng)絡中顯式編碼了圖的拓撲信息，展示了神經(jīng)網(wǎng)絡在結(jié)構(gòu)化推理任務中的潛力。

圖4：幾何深度學習中圖形的極值示例。

推理能力蘊含通用逼近（Corollary 5） 

最后研究團隊指出，如果一個網(wǎng)絡能夠執(zhí)行上述推理任務，那么它在有限精度下也必然具備通用逼近能力。

換句話說，推理能力本身就涵蓋了函數(shù)逼近的能力——而且是精確的、非近似的。這為“推理優(yōu)于逼近”的觀點提供了堅實的理論支撐。

5.理論意義與創(chuàng)新點

這項工作的意義，不僅在于提出了一個新的構(gòu)造方法，更在于它建立了一個統(tǒng)一的理論框架，將電路復雜度、可計算性理論與神經(jīng)網(wǎng)絡的表達能力緊密連接起來。

過去我們常用“通用逼近定理”來描述網(wǎng)絡的潛力，但那只是函數(shù)映射的視角；現(xiàn)在，我們有了一個能直接刻畫算法過程的工具。

這種方法的另一個亮點是推理可解釋性。由于網(wǎng)絡的計算圖與原算法的步驟一一對應，我們可以直接在網(wǎng)絡結(jié)構(gòu)中“看到”推理鏈條。這對于需要審計、驗證或調(diào)試的高風險應用（如金融合規(guī)、醫(yī)療診斷）尤為重要。

在復雜度可量化方面，研究團隊明確了網(wǎng)絡規(guī)模與算法復雜度之間的關系，使得我們可以在設計階段就預測所需的計算資源。這種可預測性為工程實現(xiàn)和硬件部署提供了堅實的基礎。

最重要的是，這項研究超越了逼近理論的局限。它不再停留在“網(wǎng)絡能否逼近某個函數(shù)”的問題上，而是直接回答“網(wǎng)絡能否精確執(zhí)行某個算法”。這為未來構(gòu)建具備可驗證推理能力的神經(jīng)網(wǎng)絡架構(gòu)打開了新的大門，也為 AI 推理的可計算性研究提供了新的坐標系。

6.未來研究方向

這項研究雖然已經(jīng)為“神經(jīng)網(wǎng)絡能否精確執(zhí)行算法”給出了堅實的理論答案，但研究團隊也清楚，這只是一個起點。未來的探索空間，既有數(shù)學上的深水區(qū)，也有工程落地的廣闊天地。

首先，是擴展到非歐幾里得與無限維輸入輸出的挑戰(zhàn)。當前的構(gòu)造主要針對歐幾里得空間中的有限維向量輸入輸出，而現(xiàn)實中的許多推理任務——比如圖結(jié)構(gòu)分析、流形上的信號處理、甚至函數(shù)空間上的算子求解——都天然處于非歐幾里得或無限維環(huán)境中。

如何在這些空間中定義“電路手術”，并保持計算圖的結(jié)構(gòu)保真，將是下一步的關鍵。這不僅涉及到拓撲與幾何的嵌入問題，還可能引入譜圖理論、核方法等工具，為神經(jīng)網(wǎng)絡的推理能力開辟新的維度。

其次，是將經(jīng)典逼近構(gòu)造（如小波、樣條）轉(zhuǎn)化為電路表示。小波分解、B樣條插值等方法在信號處理和數(shù)值分析中有著成熟的理論與高效的實現(xiàn)，如果能將它們系統(tǒng)化地轉(zhuǎn)化為電路，再映射到 ReLU 網(wǎng)絡，就能把這些“人類設計的高效基”直接注入到神經(jīng)網(wǎng)絡的結(jié)構(gòu)中。

這不僅可能帶來更緊湊的網(wǎng)絡規(guī)模，還能在特定任務上獲得更強的歸納偏置，讓網(wǎng)絡在訓練樣本有限的情況下依然保持高精度推理。

最后是結(jié)合幾何深度學習與算子學習的應用場景，幾何深度學習（Geometric Deep Learning）強調(diào)在圖、流形、群等結(jié)構(gòu)化空間中進行學習，而算子學習（Operator Learning）則關注從函數(shù)到函數(shù)的映射，例如求解偏微分方程或模擬物理系統(tǒng)。

將本研究的“算法到網(wǎng)絡”映射方法與這兩類前沿方向結(jié)合，有望構(gòu)建出既能保留推理鏈條、又能處理復雜結(jié)構(gòu)化數(shù)據(jù)的通用推理網(wǎng)絡。例如，在分子模擬中，網(wǎng)絡可以直接嵌入化學反應的算法流程；在氣候建模中，網(wǎng)絡可以精確執(zhí)行數(shù)值積分與邊界條件處理。

可以預見，這些方向的推進，將讓神經(jīng)網(wǎng)絡的推理能力從“能做”走向“能解釋、能泛化、能遷移”，并最終在科學計算、工程設計、金融建模等高價值領域釋放出更大的潛力。（END）

參考資料：https://arxiv.org/pdf/2508.18526