今天介紹的算法名叫Tarjan，同樣是一個(gè)很奇怪的名字，奇怪就對(duì)了，這也是以人名命名的。和Kosaraju算法比起來(lái)，它除了名字更好記之外，另外一個(gè)優(yōu)點(diǎn)是它只需要一次遞歸，雖然算法的復(fù)雜度是一樣的，但是常數(shù)要小一些。它的知名度也更高，在競(jìng)賽當(dāng)中經(jīng)常出現(xiàn)。

先給大家提個(gè)醒，相比于Kosaraju算法，Tarjan算法更難理解一些。所以如果你看完本文沒(méi)有搞明白的話，建議可以閱讀一下上一篇文章。這兩個(gè)算法的效果和復(fù)雜度都是一樣的，其實(shí)學(xué)會(huì)一個(gè)就可以，沒(méi)必要死磕。

算法框架

我們來(lái)思考一個(gè)問(wèn)題，對(duì)于強(qiáng)連通分量分解的算法來(lái)說(shuō)，它的核心原理是什么?

如果你看過(guò)我們之前的文章，那么這個(gè)問(wèn)題對(duì)你來(lái)說(shuō)應(yīng)該不難回答。既然是強(qiáng)連通分量，意味著分量當(dāng)中每個(gè)點(diǎn)都可以互相連通。所以我們很容易可以想到，我們可以從一個(gè)點(diǎn)出發(fā)，找到一個(gè)回路讓它再回到起點(diǎn)。這樣途中經(jīng)過(guò)的點(diǎn)就都是強(qiáng)連通分量的一部分。

但是這樣會(huì)有一個(gè)問(wèn)題，就是需要保證強(qiáng)連通分量當(dāng)中的每個(gè)點(diǎn)都被遍歷到，不能有遺漏。針對(duì)這個(gè)問(wèn)題我們也可以想到解法，比如可以用搜索算法去搜索它所有能夠達(dá)到的點(diǎn)和所有的路徑。但是這樣一來(lái)，我們又會(huì)遇到另外一個(gè)問(wèn)題。這個(gè)問(wèn)題就是強(qiáng)連通分量之間的連通問(wèn)題。

我們來(lái)看個(gè)例子：

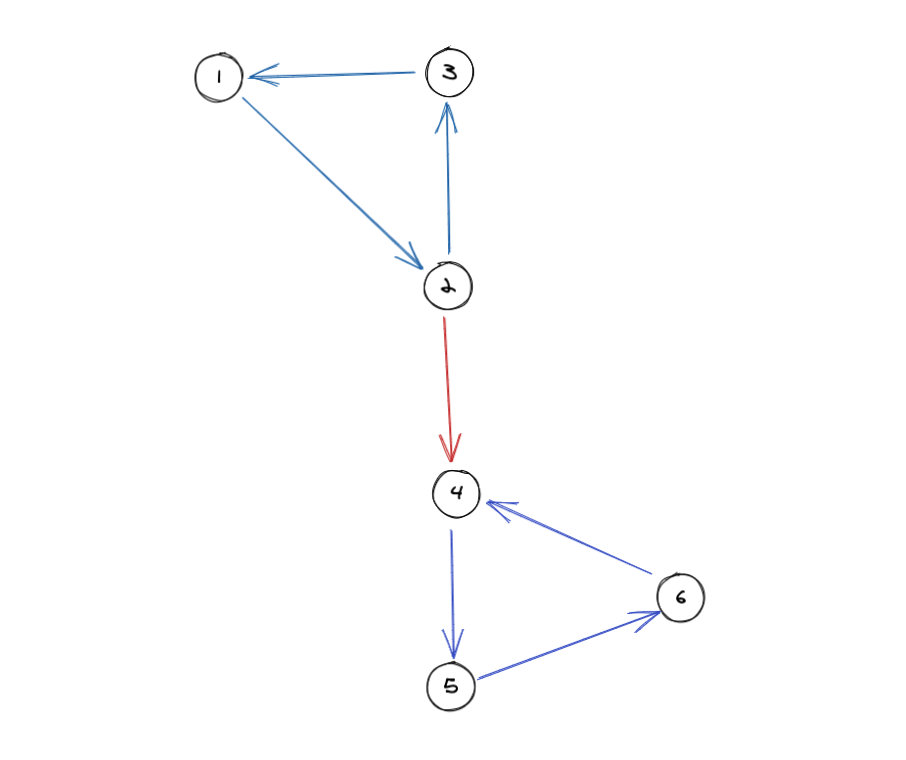
在上面這張圖當(dāng)中如果我們從點(diǎn)1出發(fā)，我們可以達(dá)到圖中的每一個(gè)點(diǎn)。但是我們會(huì)發(fā)現(xiàn)1，2，3是一個(gè)強(qiáng)連通分量，4，5，6是另外一個(gè)。當(dāng)我們尋找1所在的強(qiáng)連通分量的時(shí)候，很有可能會(huì)把4，5，6這三個(gè)點(diǎn)也帶進(jìn)來(lái)。但問(wèn)題是它們是自成分量的，并不應(yīng)該算在1的強(qiáng)連通分量當(dāng)中。

我們整理一下上面的分析和思路可以發(fā)現(xiàn)強(qiáng)連通分量分解這個(gè)算法的核心其實(shí)就是解決這兩個(gè)問(wèn)題，就是完備性問(wèn)題。完備意味著不能遺漏也不能冗余和錯(cuò)誤，我們想明白核心問(wèn)題所在之后就很容易搭建起思維框架，接下來(lái)我們?cè)賮?lái)看算法的描述會(huì)容易理解得多。

算法細(xì)節(jié)

Tarjan算法的第一個(gè)機(jī)制是時(shí)間戳，也就是在遍歷的時(shí)候?qū)γ恳粋€(gè)遍歷到的點(diǎn)打上一個(gè)值。這個(gè)值表示這是第幾個(gè)遍歷的元素。

這個(gè)應(yīng)該很好理解，我們只需要維護(hù)一個(gè)全局的變量，在遍歷的時(shí)候去讓它自增就可以了。我們來(lái)寫下Python代碼給大家演示一下：

stamp = 0 
stamp_dict = {}def dfs(u): 
    stamp_dict[u] = stamp    stamp += 1 
    for v in Graph[u]: 
        dfs(v) 

通過(guò)時(shí)間戳我們可以知道每個(gè)點(diǎn)被訪問(wèn)的順序，這個(gè)順序是正向順序。舉個(gè)例子，比如說(shuō)假設(shè)u和v兩個(gè)點(diǎn)，u的時(shí)間戳比v小。那么它們之間的關(guān)系只有兩種可能，第一種是u能夠連通到v，說(shuō)明從u到v的鏈路可以走通。第二種是u不能連通到v，這種情況不論反向的從v到u能否連通都不具有討論意義，因?yàn)樗鼈円欢ú荒芑ハ噙B通。

所以我們想要找到連通的通路還需要找到反向的路徑，在Kosaraju算法當(dāng)中我們是通過(guò)反向圖來(lái)實(shí)現(xiàn)的。在Tarjan當(dāng)中則采取了另外一種方法。因?yàn)槲覀円呀?jīng)知道各個(gè)點(diǎn)的時(shí)間戳了，我們完全可以通過(guò)時(shí)間戳來(lái)尋找反向的路徑。什么意思呢?其實(shí)很簡(jiǎn)單，當(dāng)我們?cè)诒闅vu的時(shí)候如果遇到了一個(gè)比u時(shí)間戳更小的v，那么說(shuō)明就存在一條反向的路徑從u通向v。如果v這時(shí)候還沒(méi)有出棧，意味著v是u的上游的話，那么也就說(shuō)明存在一條路徑從v通向u。這樣就說(shuō)明了u和v可以互相連通。

既然找到了一對(duì)互相連通的u和v，那么我們需要把它們記錄下來(lái)。但問(wèn)題是我們?cè)趺粗烙涗浀绞裁磿r(shí)候?yàn)橹鼓?這個(gè)邊界在哪里?Tarjan算法設(shè)計(jì)了另外一個(gè)巧妙的機(jī)制解決了這個(gè)問(wèn)題。

這個(gè)機(jī)制就是low機(jī)制，low[u]表示u這個(gè)點(diǎn)能夠連通到的所有的點(diǎn)的時(shí)間戳的最小值。時(shí)間戳越小說(shuō)明在搜索樹當(dāng)中的位置越高，也可以理解成u能夠連通到的處在搜索樹中最高的點(diǎn)。那么很明顯了，這個(gè)點(diǎn)就是u這個(gè)點(diǎn)所在強(qiáng)連通分量所在搜索樹某一棵子樹的樹根。

這里可能有一點(diǎn)點(diǎn)繞，我們?cè)賮?lái)看張圖：

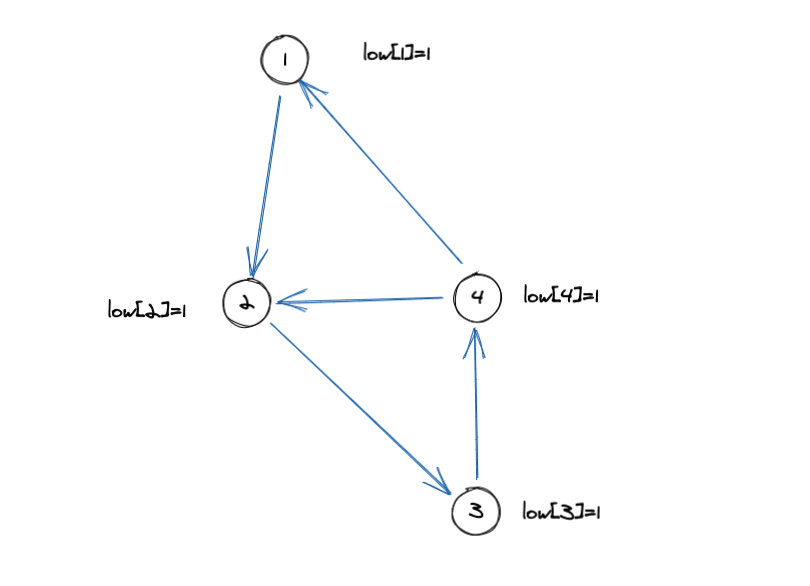
圖中節(jié)點(diǎn)所在的序號(hào)就是遞歸遍歷的時(shí)間戳，我們可以發(fā)現(xiàn)對(duì)于圖上的每個(gè)點(diǎn)來(lái)說(shuō)它們的low值都是1。很明顯1這個(gè)點(diǎn)在搜索樹當(dāng)中是2，3，4這三個(gè)點(diǎn)的祖先。也就是說(shuō)這一個(gè)強(qiáng)連通分量的遍歷是從1這個(gè)點(diǎn)開始的。當(dāng)1這個(gè)點(diǎn)出棧的時(shí)候，意味著以1位樹根的子樹已經(jīng)遍歷完了，所有可能存在的強(qiáng)連通分量也都已經(jīng)找完了。

這就帶來(lái)了另外一個(gè)問(wèn)題，我們假設(shè)當(dāng)前點(diǎn)是u，我們?nèi)绾沃纔這個(gè)點(diǎn)是否是圖中1這樣的樹根呢?有沒(méi)有什么辦法可以標(biāo)記出來(lái)呢?

當(dāng)然是有的，這樣的點(diǎn)有一個(gè)特性就是它們的時(shí)間戳等于它們的low。所以我們可以用一個(gè)數(shù)組維護(hù)找到的強(qiáng)連通分量，當(dāng)這些強(qiáng)連通分量能夠遍歷到的樹根出棧的時(shí)候，把數(shù)組清空。

我們把上面的邏輯整理一下就可以寫出代碼來(lái)了：

scc = [] 
stack = [] 
def tarjan(u):    dfn[u], low[u] = stamp, stamp    stamp += 1 
 stack.append(u) 
        for v in Graph[u]: 
        if not dfn[v]: 
            tarjan(v)            low[u] = min(low[u], low[v])        elif v in stack: 
         low[u] = min(low[u], dfn[v])       if dfn[u] == low[u]: 
        cur = []        # 棧中u之后的元素是一個(gè)完整的強(qiáng)連通分量        while True: 
            cur.append(stack[-1]) 
            stack.pop() 
            if cur[-1] == u: 
                break 
        scc.append(cur) 

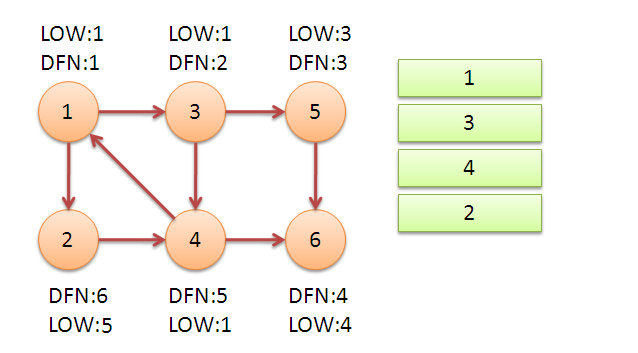
最后，我們來(lái)看一下之前講過(guò)的經(jīng)典例子：

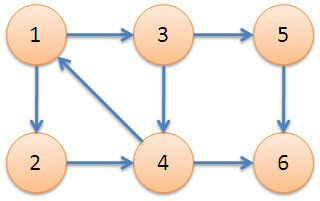
首先我們從1點(diǎn)開始，一直深搜到6結(jié)束，當(dāng)遍歷到6的時(shí)候，DFN[6]=4，low[6]=4，當(dāng)6出棧時(shí)滿足條件，6獨(dú)立稱為一個(gè)強(qiáng)連通分量。

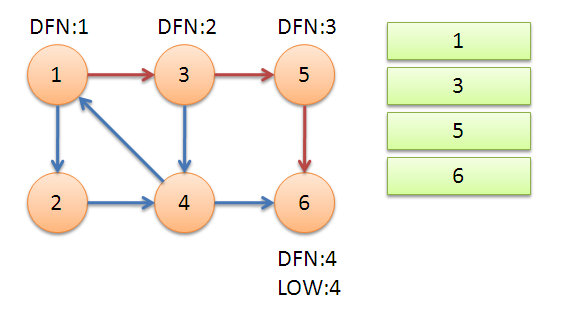
同理，當(dāng)5退出的時(shí)候也同樣滿足條件，我們得到了第二個(gè)強(qiáng)連通分量。

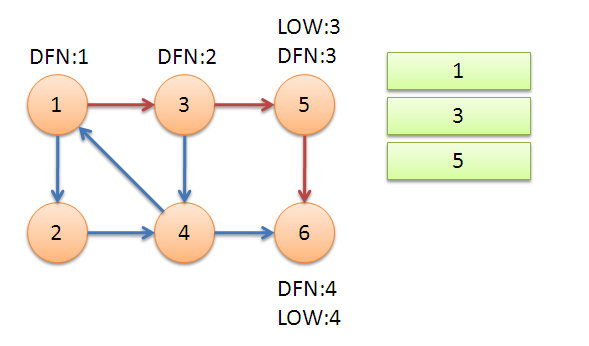
接著我們回溯到節(jié)點(diǎn)3，節(jié)點(diǎn)3還可以遍歷到節(jié)點(diǎn)4，4又可以連向1。由于1點(diǎn)已經(jīng)在棧中，所以不會(huì)繼續(xù)遞歸1點(diǎn)，只會(huì)更新low[4] = 1，同樣當(dāng)4退出的時(shí)候又會(huì)更新3，使得low[3] = 1。

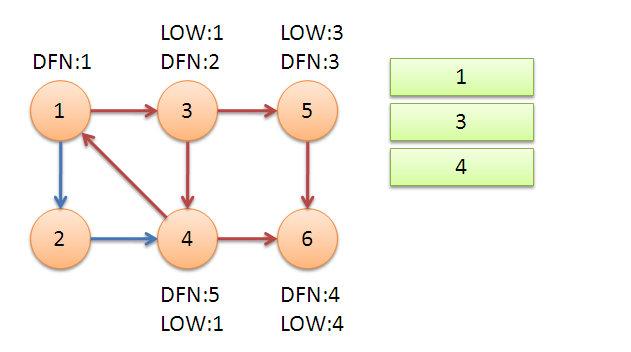
最后我們返回節(jié)點(diǎn)1，通過(guò)節(jié)點(diǎn)1遍歷到節(jié)點(diǎn)2。2能連通的4點(diǎn)已經(jīng)在棧中，并且DFN[4] > DFN[2]，所以并不會(huì)更新2點(diǎn)。再次回到1點(diǎn)之后，1點(diǎn)沒(méi)有其他點(diǎn)可以連通，退出。退出的時(shí)候發(fā)現(xiàn)low[1] = DFN[1]，此時(shí)棧中剩下的4個(gè)元素全部都是強(qiáng)連通分量。

到這里，整個(gè)算法流程的介紹就算是結(jié)束了，希望大家都可以enjoy今天的內(nèi)容。