奧賽冠軍都做不對(duì)的題,卻被拿來考ML模型?GPT-3:我不行
為了衡量機(jī)器學(xué)習(xí)模型的數(shù)學(xué)求解能力,來自 UC 伯克利和芝加哥大學(xué)的研究者提出了一個(gè)包含 12, 500 道數(shù)學(xué)競(jìng)賽難題的新型數(shù)據(jù)集 MATH,以及幫助模型學(xué)習(xí)數(shù)學(xué)基礎(chǔ)知識(shí)的預(yù)訓(xùn)練數(shù)據(jù)集 AMPS。研究發(fā)現(xiàn),即使是大參數(shù)的 Transformer 模型準(zhǔn)確率也很低。
許多學(xué)術(shù)研究探討數(shù)學(xué)問題求解,但對(duì)于計(jì)算機(jī)而言這超出了其能力范疇。那么機(jī)器學(xué)習(xí)模型是否具備數(shù)學(xué)問題求解能力呢?
來自加州大學(xué)伯克利分校和芝加哥大學(xué)的研究者為此創(chuàng)建了一個(gè)新型數(shù)據(jù)集 MATH。該數(shù)據(jù)集包含 12, 500 道數(shù)學(xué)競(jìng)賽難題,每個(gè)數(shù)學(xué)題都有完整的逐步求解過程,可用來教機(jī)器學(xué)習(xí)模型生成答案和解釋。為了促進(jìn)未來研究,提升模型在 MATH 數(shù)據(jù)集上的準(zhǔn)確率,研究者還創(chuàng)建了另一個(gè)大型輔助預(yù)訓(xùn)練數(shù)據(jù)集,它可以教模型數(shù)學(xué)基礎(chǔ)知識(shí)。
盡管通過這些方法提升了模型在 MATH 數(shù)據(jù)集上的準(zhǔn)確率,但實(shí)驗(yàn)結(jié)果表明,準(zhǔn)確率仍然很低,即使 Transformer 模型也不例外。研究者還發(fā)現(xiàn),僅靠增加預(yù)算和模型參數(shù)量并不能實(shí)現(xiàn)強(qiáng)大的數(shù)學(xué)推理能力。擴(kuò)展 Transformer 能夠自動(dòng)解決大多數(shù)文本任務(wù),但目前仍無法解決 MATH 問題。
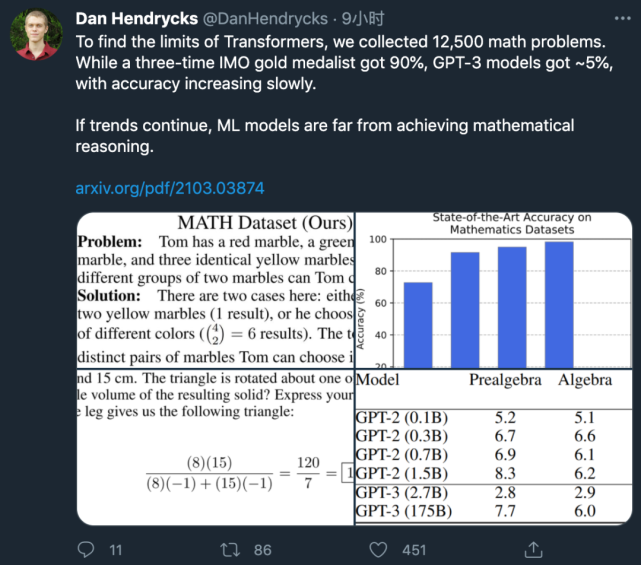
該研究第一作者 Dan Hendrycks 發(fā)推表示:
國(guó)際數(shù)學(xué)奧林匹克競(jìng)賽(IMO)三金得主能達(dá)到 90% 的準(zhǔn)確率,而 GPT-3 的準(zhǔn)確率只能達(dá)到約 5%。
如果這一趨勢(shì)持續(xù)下去,那么機(jī)器學(xué)習(xí)模型距離獲得數(shù)學(xué)推理能力還很遙遠(yuǎn)。
數(shù)據(jù)集
這部分介紹兩個(gè)新型數(shù)據(jù)集,一個(gè)是用于測(cè)試模型數(shù)學(xué)問題求解能力的 MATH 數(shù)據(jù)集,另一個(gè)是用于輔助預(yù)訓(xùn)練的 AMPS 數(shù)據(jù)集。
MATH 數(shù)據(jù)集
MATH 數(shù)據(jù)集包含 12, 500 個(gè)數(shù)學(xué)問題(其中 7500 個(gè)屬于訓(xùn)練集,5000 個(gè)屬于測(cè)試集),這些問題收集自 AMC 10、AMC 12、AIME 等數(shù)學(xué)競(jìng)賽(這些數(shù)學(xué)競(jìng)賽已經(jīng)持續(xù)數(shù)十年,旨在評(píng)估美國(guó)最優(yōu)秀的年輕數(shù)學(xué)人才的數(shù)學(xué)問題求解能力)。與大多數(shù)之前的研究不同,MATH 數(shù)據(jù)集中的大部分問題無法通過直接應(yīng)用標(biāo)準(zhǔn) K-12 數(shù)學(xué)工具來解決,人類解決這類問題通常需要用到問題求解技術(shù)和「啟發(fā)式」方法。
基于這些數(shù)學(xué)問題,模型可以學(xué)習(xí)多種有用的問題求解啟發(fā)式方法,且每個(gè)問題都有逐步求解過程和最終答案。具備逐步求解過程的問題示例參見下圖 1:

該數(shù)據(jù)集的創(chuàng)建涉及以下重要步驟:
問題分類:該數(shù)據(jù)集中的問題難度不同,并涉及多個(gè)主題,包括算術(shù)、代數(shù)、數(shù)論、計(jì)數(shù)與概率、幾何、中級(jí)代數(shù)、預(yù)備微積分。研究者按照對(duì)人類而言從易到難的程度將問題難度等級(jí)標(biāo)注為 1-5。
格式化:使用 LATEX 和 Asymptote 矢量圖語(yǔ)言將數(shù)學(xué)問題及其解進(jìn)行統(tǒng)一格式化。
自動(dòng)評(píng)估生成的答案:MATH 數(shù)據(jù)集的獨(dú)特設(shè)計(jì)使得研究者可以自動(dòng)評(píng)估模型生成的答案,即使模型輸出空間非常大。
人類性能:為了估計(jì)人類性能,研究者從 MATH 測(cè)試集中隨機(jī)采樣了 20 個(gè)問題,交由高校學(xué)生回答。一位不喜歡數(shù)學(xué)的參與者答對(duì)了 8 道題(準(zhǔn)確率 40%),兩位喜歡數(shù)學(xué)的參與者分別答對(duì)了 14 題和 15 題,一位在 AMC 10 數(shù)學(xué)競(jìng)賽中拿到滿分并多次參加 USAMO 競(jìng)賽的參與者答對(duì)了 18 道題,一位 IMO 三金得主也答對(duì)了 18 道題(準(zhǔn)確率 90%)。這說明 MATH 數(shù)據(jù)集中的數(shù)學(xué)問題對(duì)于人類而言也是有一定難度的。
AMPS 數(shù)據(jù)集(可汗學(xué)院 + Mathematica)
預(yù)訓(xùn)練數(shù)據(jù)會(huì)對(duì)性能產(chǎn)生極大影響,而數(shù)學(xué)是在線文本的一小部分,于是該研究創(chuàng)建了一個(gè)大型多樣化的數(shù)學(xué)預(yù)訓(xùn)練語(yǔ)料庫(kù)。該預(yù)訓(xùn)練數(shù)據(jù)集 Auxiliary Mathematics Problems and Solutions (AMPS) 包括許多問題及 LATEX 格式的逐步求解過程。
AMPS 數(shù)據(jù)集包含 10 萬個(gè)收集自可汗學(xué)院的數(shù)學(xué)問題,和約 500 萬通過手動(dòng)設(shè)計(jì) Mathematica 腳本生成的問題。該研究使用 Mathematica 的計(jì)算機(jī)代數(shù)系統(tǒng)生成數(shù)學(xué)問題,是為了便于操作分?jǐn)?shù)、超越數(shù)和解析函數(shù)。
這些問題涉及多個(gè)主題,包括代數(shù)、微積分、計(jì)數(shù)與統(tǒng)計(jì)、幾何、線性代數(shù),以及數(shù)論(參見下表 1)。

實(shí)驗(yàn)
模型性能
研究者通過實(shí)驗(yàn)調(diào)查了模型在 MATH 數(shù)據(jù)集上的性能,發(fā)現(xiàn)即使最優(yōu)模型的準(zhǔn)確率也很低。此外,與大多數(shù)基于文本的數(shù)據(jù)集不同,該數(shù)據(jù)集上的準(zhǔn)確率增速隨著模型規(guī)模的擴(kuò)大而越來越慢。如果這一趨勢(shì)繼續(xù),則要想在 MATH 數(shù)據(jù)集上取得較大進(jìn)展,我們需要的不只是模型擴(kuò)展,而是算法改進(jìn)。
下表 2 表明,最小模型 GPT-2(0.1 billion 參數(shù)量,基線模型)在 MATH 數(shù)據(jù)集多個(gè)主題上的平均準(zhǔn)確率為 5.4%,而 GPT-2(1.5 billion 參數(shù)量,參數(shù)量是基線模型的 15 倍)的平均準(zhǔn)確率為 6.9%,相比基線提升了 28%。這表明與大部分其它基于文本的任務(wù)不同,在 MATH 數(shù)據(jù)集上增加模型參數(shù)確實(shí)有所幫助,但模型的絕對(duì)準(zhǔn)確率仍然很低,且增速緩慢。
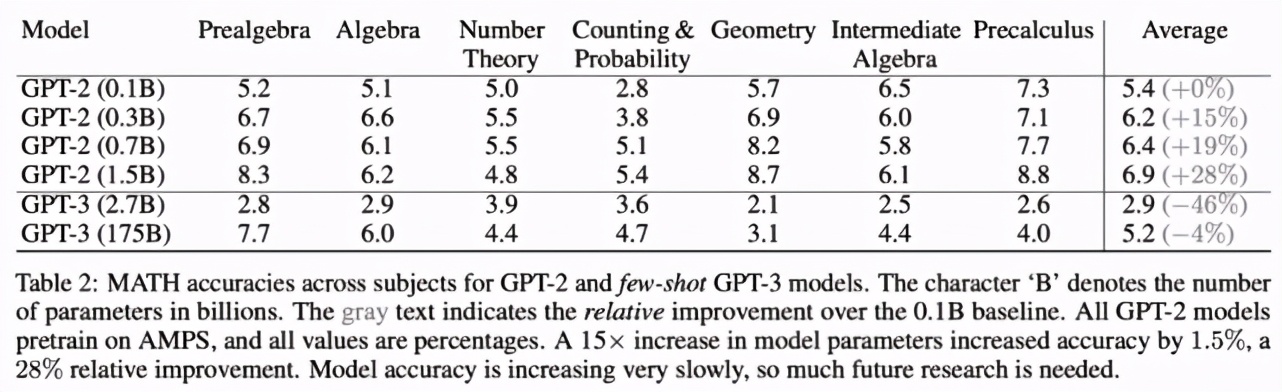
此外,研究者測(cè)試了使用 AMPS 預(yù)訓(xùn)練的效果。未經(jīng) AMPS 預(yù)訓(xùn)練時(shí),GPT-2 (1.5B) 模型在 MATH 數(shù)據(jù)集上的準(zhǔn)確率為 5.5%;而經(jīng)過 AMPS 預(yù)訓(xùn)練后,GPT-2 (1.5B) 在 MATH 數(shù)據(jù)集上的準(zhǔn)確率為 6.9%(參見表 2),準(zhǔn)確率提升了 25%。也就是說,AMPS 預(yù)訓(xùn)練對(duì)準(zhǔn)確率的提升效果相當(dāng)于參數(shù)量 15 倍增加的效果,這表明 AMPS 預(yù)訓(xùn)練數(shù)據(jù)集是有價(jià)值的。
逐步求解
研究者對(duì)逐步求解過程進(jìn)行了實(shí)驗(yàn),發(fā)現(xiàn)模型在得到答案前先生成逐步求解過程會(huì)導(dǎo)致準(zhǔn)確率下降。研究者利用 GPT-2 (1.5B) 進(jìn)行評(píng)估,發(fā)現(xiàn)模型性能有所下降,從 6.9% 下降到了 5.3%。
研究者還對(duì)這些生成的逐步求解過程進(jìn)行了定性評(píng)估,發(fā)現(xiàn)盡管很多步驟看似與問題相關(guān),但其實(shí)存在邏輯問題。示例參見下圖 3、4:

圖 3:?jiǎn)栴}、GPT-2 (1.5B) 模型生成的逐步解、真值解。

圖 4:?jiǎn)栴}、生成解和真值解示例。
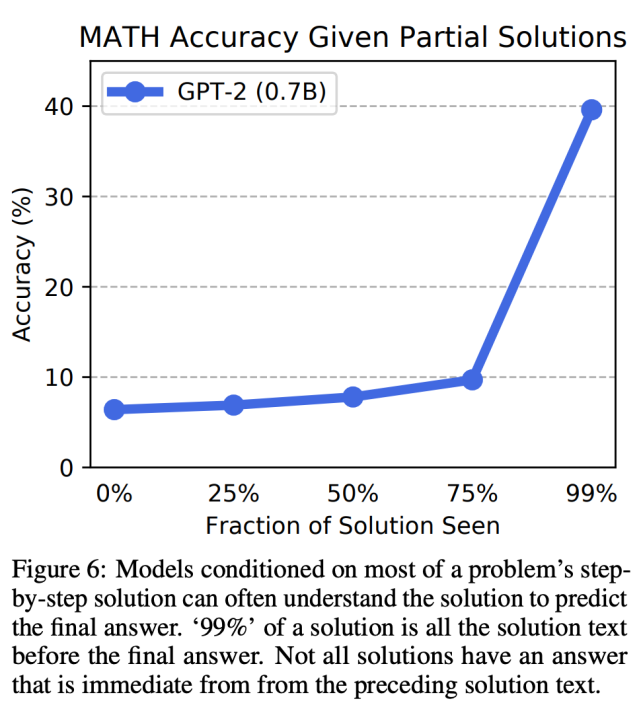
不過,研究人員發(fā)現(xiàn)逐步求解仍能帶來一定好處:提供部分真值逐步求解過程可以提升性能,在訓(xùn)練過程中為模型提供逐步求解過程可以提升準(zhǔn)確率。下圖 6 展示了 GPT-2 (0.7B) 模型使用不同部分求解過程的準(zhǔn)確率變化。