進能形式邏輯,退能四則運算,MAmmoT讓LLM成為數學通才
數學推理是現代大型語言模型(LLM)的一項關鍵能力。盡管這一領域近來進展不錯,但閉源和開源 LLM 之間仍然存在明顯的差距——GPT-4、PaLM-2 和 Claude 2 等閉源模型主宰了 GSM8K 和 MATH 等常用數學推理基準,而 Llama、Falcon 和 OPT 等開源模型在所有基準上都大幅落后。
為了解決這一問題,研究界正在兩個方向進行努力:
(1)Galactica 和 MINERVA 等持續型預訓練方法,其能在超過千億 token 的數學相關網絡數據上對 LLM 進行持續訓練。這一方法能提升模型的一般科學推理能力,但代價是高計算成本。
(2)拒絕采樣微調(RFT)和 WizardMath 等針對特定數據集進行微調的方法,即使用特定數據集的監督數據對 LLM 進行微調。盡管這些方法能提升在具體領域內的性能,但無法泛化到微調數據之外的更廣范圍的數學推理任務。舉個例子,RFT 和 WizardMath 可將在 GSM8K(這是微調數據集之一)上的準確度提升 30% 以上,但卻有損在 MMLU-Math 和 AQuA 等領域外數據集上的準確度——使之降低多達 10%。
近日,來自滑鐵盧大學和俄亥俄州立大學等機構的研究團隊提出了一種輕量級卻又可泛化的數學指令微調方法,可用于增強 LLM 的一般性(即不限于微調任務)數學推理能力。
之前已有的方法關注的重點是思維鏈(CoT)方法,即通過一步步的自然語言描述來解決數學問題。這種方法的通用性很強,可覆蓋大多數數學科目,但卻在計算精度和復雜的數學或算法推理過程(例如求解二次方程根和計算矩陣特征值)方面存在困難。
相比之下,像思維程序(PoT)和 PAL 這樣的代碼格式 prompt 設計方法則是利用外部工具(即 Python 解釋器)來大幅簡化數學求解過程。這種方法是將計算過程卸載到外部 Python 解釋器來求解復雜的數學和算法推理(例如使用 sympy 求解二次方程或使用 numpy 計算矩陣特征值)。但是,PoT 難以應對更抽象的推理場景,比如常識推理、形式邏輯和抽象代數,尤其是沒有內置的 API 時。
為了取 CoT 和 PoT 兩種方法之長,該團隊引入了一個新的數學混合指令微調數據集 MathInstruct,其有兩大主要特性:(1) 廣泛涵蓋不同的數學領域和復雜程度,(2) 將 CoT 和 PoT 原理組合到了一起。
MathInstruct 基于七個現有的數學原理數據集和六個新整理出的數據集。他們使用 MathInstruct 微調了不同大小(從 7B 到 70B)的 Llama 模型。他們將所得到的模型稱為 MAmmoTH 模型,結果發現 MAmmoTH 的能力是前所未有的,就像是一個數學通才。
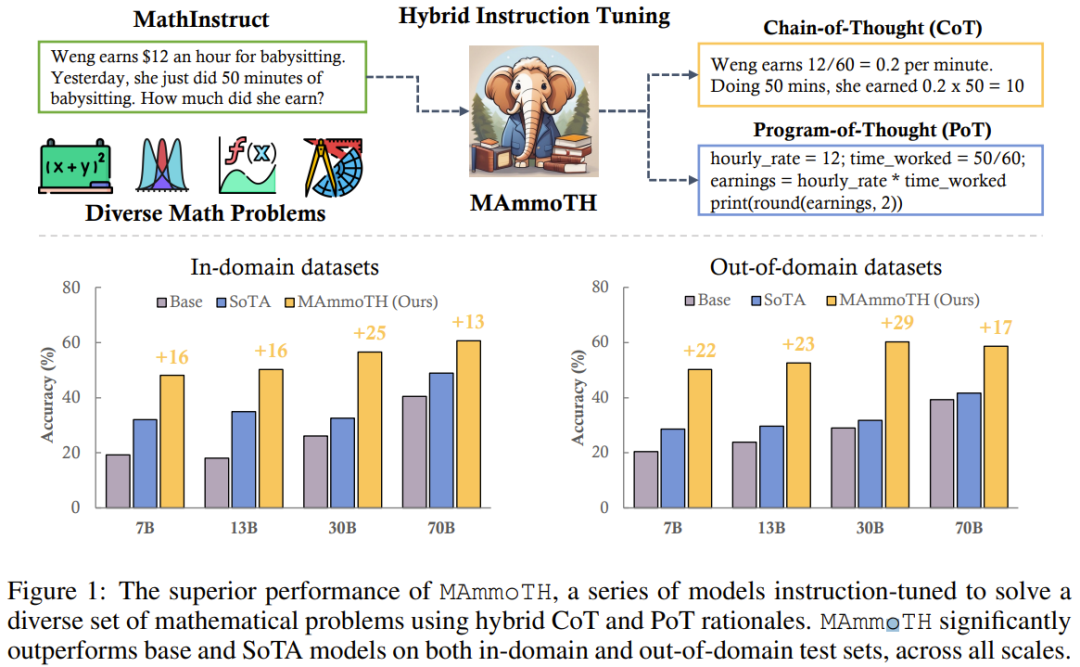
為了評估 MAmmoTH,該團隊使用了一系列評估數據集,包括領域內的測試集(GSM8K、MATH、AQuA-RAT、NumGLUE)和領域外的測試集(SVAMP、SAT、MMLU-Math、Mathematics、SimulEq)。
結果發現,相比于之前的方法,MAmmoTH 模型能更好地泛化用于領域外數據集,并能大幅提升開源 LLM 的數學推理能力。
值得注意的是,在常用的競賽級 MATH 數據集上,7B 版本的 MAmmoTH 模型能以 3.5 倍的優勢(35.2% vs 10.7%)擊敗 WizardMath(這是 MATH 上之前最佳的開源模型),而 34B MAmmoTH-Coder(在 Code Llama 上進行過微調)甚至可以勝過使用 CoT 的 GPT-4。
這項研究的貢獻可以總結成兩個方面:(1) 從數據工程方面看,他們提出了一個高質量的數學指令微調數據集,其中包含多種不同的數學問題和混合原理。(2) 從建模方面講,他們訓練和評估了大小從 7B 到 70B 的 50 多個不同的新模型和基準模型,以此探究了不同數據源和輸入-輸出格式的影響。
結果發現,MAmmoTH 和 MAmmoTH-Coder 等新模型在準確度方面都顯著優于之前的開源模型。

- 論文:https://arxiv.org/pdf/2309.05653.pdf
- 代碼:https://github.com/TIGER-AI-Lab/MAmmoTH
- 數據集與模型:https://huggingface.co/datasets/TIGER-Lab/MathInstruct
該團隊已經發布了他們整理得到的數據集,并開源了新方法的代碼,也在 Hugging Face 發布了訓練好的不同大小的模型。
新提出的方法
整理一個多樣化的混合指令微調數據集
該團隊的目標是編制一份列表,其中包含高質量且多樣化的數學指令微調數據集,其應具有兩個主要特征:(1) 廣泛涵蓋不同的數學領域和復雜程度,(2) 將 CoT 和 PoT 原理組合到一起。
對于第一個特征,他們首先選出了一些使用廣泛并且涉及不同數學領域和復雜程度的高質量數據集,比如 GSM8K、MATH、AQuA、Camel 和 TheoremQA。然后他們注意到現有數據集沒有大學水平的數學知識,比如抽象代數和形式邏輯。針對這個問題,他們借助于網上找到的少量種子示例,使用 GPT-4 為 TheoremQA 中的問題合成 CoT 原理并通過 Self-Instruct 創建「問題-CoT」配對。
對于第二個特征,將 CoT 和 PoT 原理組合到一起可以提升數據集的多功能性,使其訓練的模型有能力解決不同類型的數學問題。但是,大多數現有數據集提供的程序原理有限,導致 CoT 和 PoT 原理之間不平衡。為此,該團隊又用到了 GPT-4,來為所選數據集補充 PoT 原理,包括 MATH、AQuA、 GSM8K 和 TheoremQA。然后再對這些 GPT-4 合成的程序進行過濾,做法是將它們的執行結果與人類標注的基本真值進行比較,這能確保所添加的都是高質量的原理。
遵循這些準則,他們創建了一個新的數據集 MathInstruct,詳見下表 1。
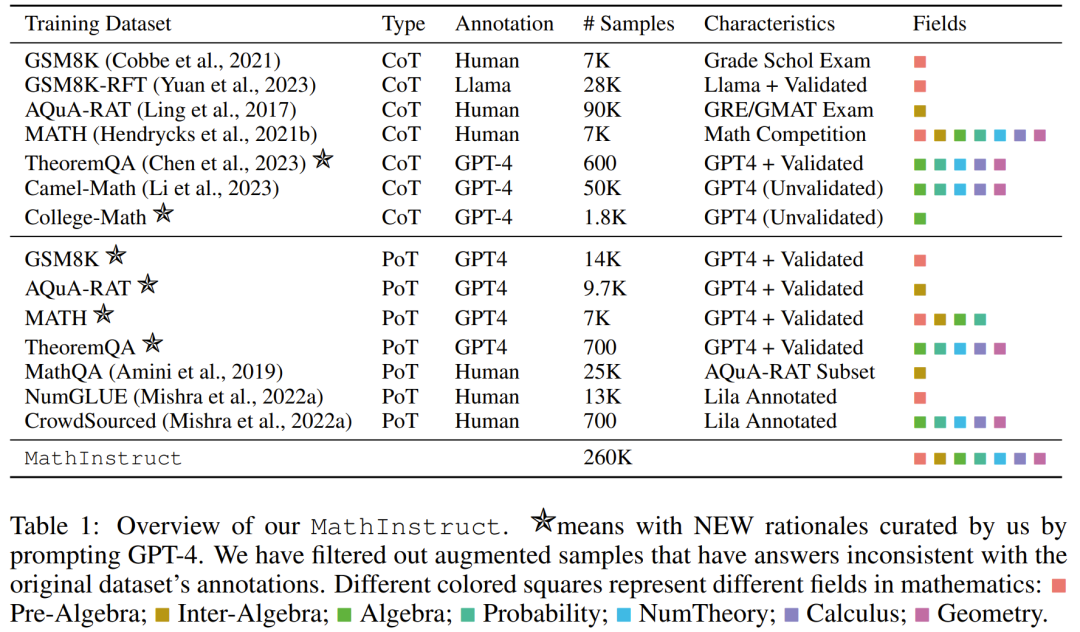
其中包含 26 萬對 (指令,響應),覆蓋廣泛的核心數學領域(算術、代數、概率學、微積分和幾何等),包含混合的 CoT 和 PoT 原理,并有不同的語言和難度。
訓練設置
MathInstruct 的所有子集都統一成了類似 Alpaca 的指令數據集的結構。這種標準化操作可確保微調得到的模型能夠一致地處理數據,無論原始數據集格式如何。
在基礎模型方面,該團隊的選擇是 Llama-2 和 Code Llama。
通過在 MathInstruct 上進行微調,他們得到了 7B、13B、34B 和 70B 等大小不同的模型。
實驗
評估數據集
為了評估模型的數學推理能力,該團隊選擇了一些評估數據集,見下表 2,其中包含許多不同領域內和領域外樣本,涉及多個不同數學領域。
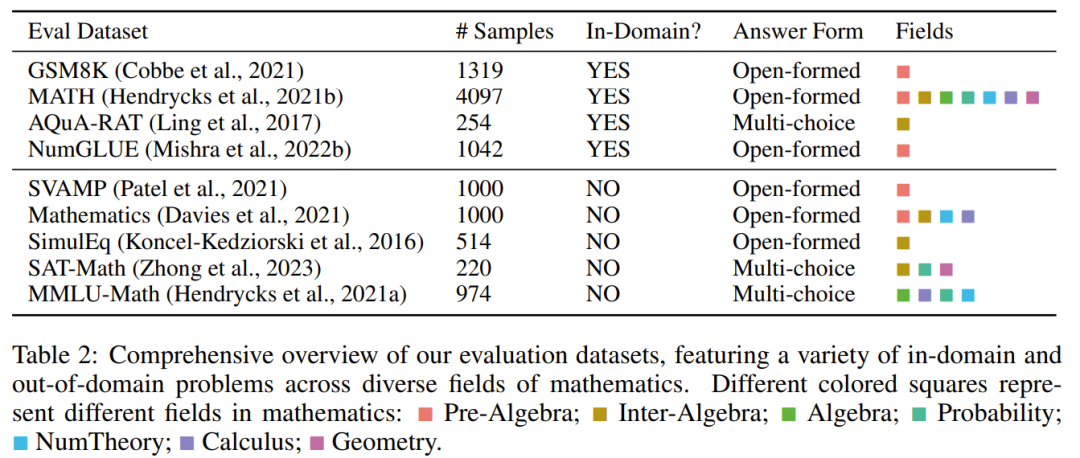
這個評估數據集也包含不同的難度等級,包括小學、中學和大學水平。某些數據集甚至包括形式邏輯和常識推理。
所選擇的評估數據集既有開放式問題,也有多項選擇題。
對于開放式問題(如 GSM8K 和 MATH),研究者采用了 PoT 解碼,因為大多數這類問題可以通過程序求解。、
對于多項選擇題(如 AQuA 和 MMLU),研究者采用了 CoT 解碼,因為這個數據集中的大部分問題都可以通過 CoT 更好地處理。
CoT 解碼不需要任何觸發詞,而 PoT 解碼需要一個觸發語:「Let’s write a program to solve the problem」。
主要結果
下表 3 和表 4 分別報告了在領域內外數據上的結果。
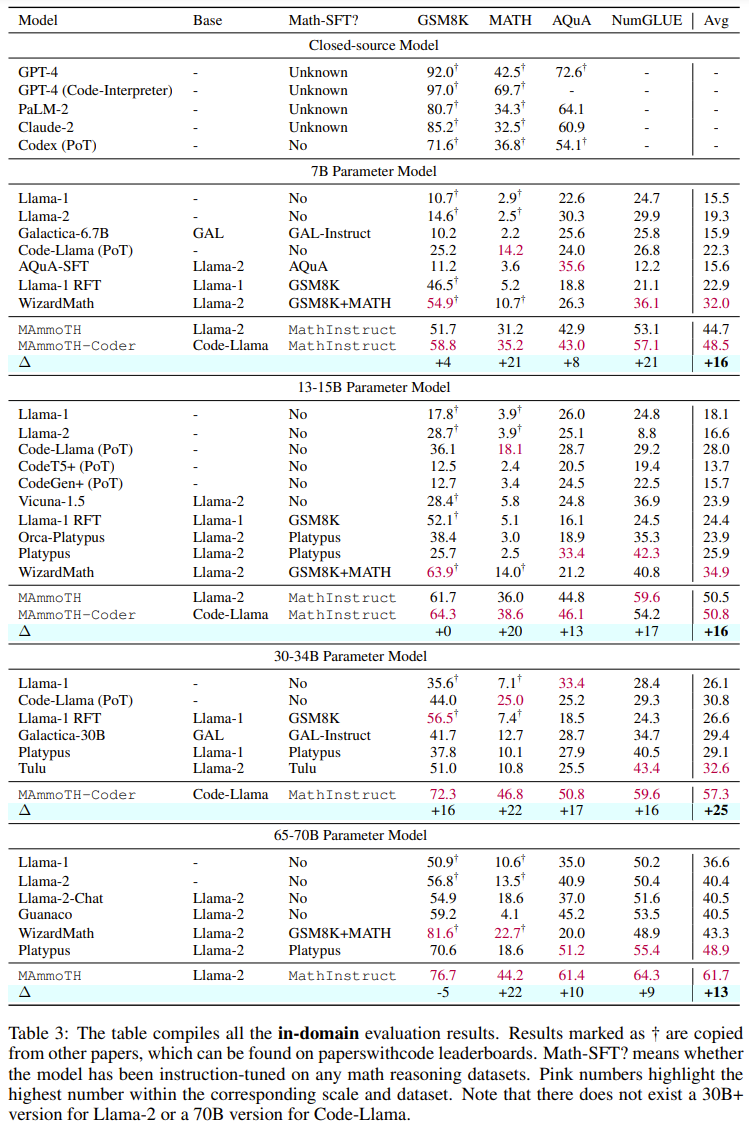

總體而言,在不同的模型大小上,MAmmoTH 和 MAmmoTH-Coder 都優于之前最佳的模型。新模型在領域外數據集上取得的性能增長多于在領域內數據集上所獲增長。這些結果表明新模型確實有成為數學通才的潛力。MAmmoTH-Coder-34B 和 MAmmoTH-70B 在一些數據集上的表現甚至超過了閉源 LLM。
研究者也比較了使用不同基礎模型的情況。具體來說,他們實驗了 Llama-2 和 Code-Llama 這兩種基礎模型。從上面兩張表可以看出,Code-Llama 整體上要優于 Llama-2,尤其是在領域外數據集上。MAmmoTH 和 MAmmoTH-Coder 之間的差距甚至可達 5%。
在數據源上的消融研究
他們通過消融研究探索了性能增益的來源。為了更好地理解 MAmmoTH 相對于已有基準模型的優勢的來源,研究者進行了一系列對照實驗,結果如下圖 2 所示。
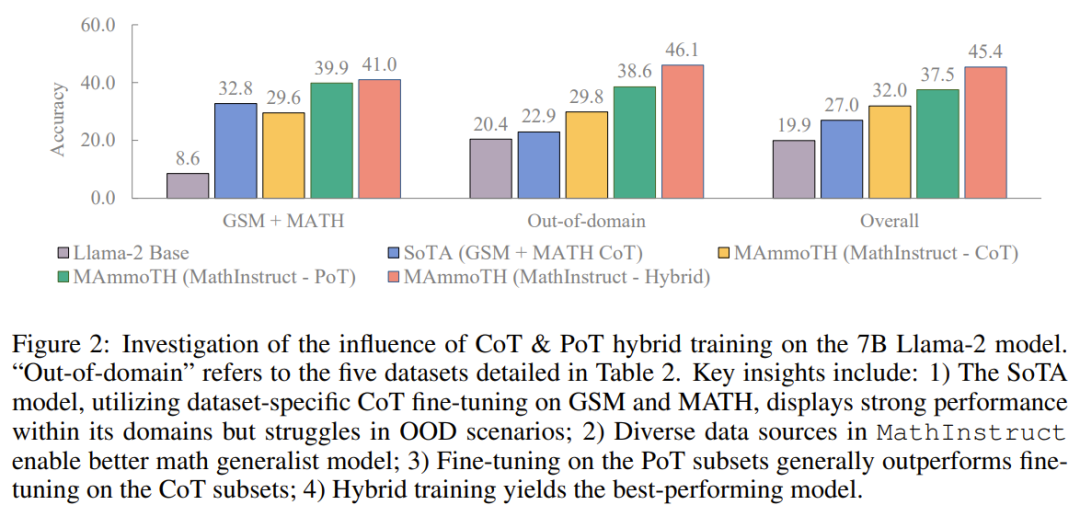
總結起來,MAmmoTH 的顯著性能優勢可以歸功于:1) 涵蓋不同的數學領域和復雜程度的多樣化數據源,2) CoT 和 PoT 指令微調的混合策略。
他們也研究了主要子集的影響。對于用于訓練 MAmmoTH 的 MathInstruct 的多樣化來源,理解各個來源對模型整體性能的貢獻程度也很重要。他們關注的重點是四個主要子集:GSM8K、MATH、 Camel 和 AQuA。他們進行了一項實驗:逐漸將每個數據集添加到訓練中,并將性能與在整個 MathInstruct 上微調的模型進行比較。
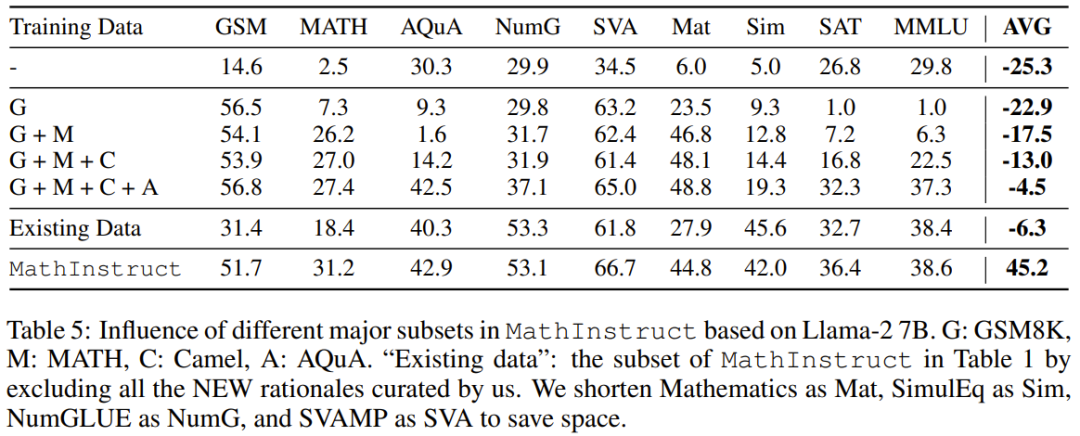
從表 5 的結果可以看到,如果一開始訓練的數據集不夠多樣化(比如只有 GSM8K 時),整體的泛化能力非常差:模型只擬合了分布內的數據,難以解答 GSM 問題之外的問題。
這些結果凸顯了多樣化數據源對 MAmmoTH 的重要影響,它們是讓 MAmmoTH 成為數學通才的核心關鍵。這些結果也貢獻了寶貴的見解,能為我們未來的數據整理收集工作提供指導比如我們應該總是收集多樣化的數據,避免只收集特定類型的數據。


































