本工作被人工智能頂級會議 NeurIPS 2024 接收。在諸如推薦系統、展示廣告等多數實際應用中，所收集的數據往往包含缺失值，并且這些缺失值通常并非隨機缺失，這會使模型的預測性能變差。一些現有的估計量和正則化器試圖實現無偏估計以提升模型的預測性能。然而，當傾向得分趨于零時，這些方法的方差和泛化誤差界通常是無界的，從而損害了它們的穩定性和魯棒性。在本文中，我們首先從理論上揭示了正則化技術的局限性。此外，我們進一步闡明，對于廣義形式的估計器，其無偏性必然會導致方差和泛化誤差無界。這些一般性規律啟示我們，預估模型的設計并非僅僅關乎消除偏差、減小方差或者簡單地實現偏差-方差的權衡。我們基于這些理論發現，從一個全新的視角重新審視對于非隨機缺失數據預估建模的本質——偏差和方差的定量聯合優化。網商銀行智能營銷團隊提出細粒度動態學習框架來聯合優化偏差和方差，該框架能夠依據預先定義的目標函數為每個用戶-商品對自適應地選擇合適的估計器。通過這種操作，模型的泛化誤差界和方差降低并從理論層面保證了預估模型方差和泛化誤差有界，進一步提高模型在隨機缺失數據上的泛化能力。

論文題目：Fine-Grained Dynamic Framework for Bias-Variance Joint Optimization on Data Missing Not at Random

論文連接：https://openreview.net/forum?id=gLoe70Tn8V&referrer=%5BAuthor%20Console%5D(%2Fgroup%3Fid%3DNeurIPS.cc%2F2024%2FConference%2FAuthors%23your-submissions)

一、糾偏推薦背景介紹

在幾乎所有的實際應用場景中，我們所收集的數據存在一定概率的部分缺失情況。具有相同缺失概率的特殊情形被稱為隨機缺失（MAR）。然而，在在線推薦、搜索和展示廣告領域，存在大量非隨機缺失（MNAR）的點擊、轉化和評級記錄，樣本缺失的概率各不相同，即存在傾向性。例如，在推薦系統中，用戶通常會點擊他們可能購買的物品，而對購買意愿較低的其他物品則予以忽略。因此，所觀察到的點擊和轉化數據屬于 MNAR 類型，并非代表性樣本。當使用 MNAR 數據來訓練模型時，該模型在 MAR 數據上的預測表現通常難以令人接受。這是因為 MNAR 數據給預測模型引入了樣本選擇偏差。

為了消除樣本選擇偏差，研究人員提出了許多偏差校正的估計器（如基于誤差插補的（EIB）方法、逆傾向加權（IPW/IPS）技術、雙重魯棒（DR）方法等）。然而，在幾乎所有的偏差校正方法中，較小的傾向性導致了高方差和泛化誤差界。因此，研究者提出了各種方法來降低估計方差并提高模型穩定性。盡管如此，當傾向性趨于零時，它們仍然具有無窮的方差和泛化邊誤差界，這對于模型的泛化性能會產生較大的影響。對于由小傾向性引起的高方差和泛化邊界，一些方法通過犧牲無偏性而采用歸一化技術，例如，歸一化 IPS（SNIPS），穩定 DR（SDR）。此外，之前的大多數工作只關注通過設計估計器或正則化器來減少方差或消除偏差，而忽視了估計器設計中偏差-方差的關系和本質。

二、正則化技術和目前糾偏估計器的局限性

非隨機缺失數據

定義用戶集合和商品集合為 U={u_1,u_2,?,u_M }和 I={i_1,i_2,?,i_N }。所有用戶-商品對的集合表示為 D=U×I，標簽矩陣和預估矩陣表示為 Y∈R^(M×N)和 Y ?∈R^(M×N)，其中預測任務包含用戶評分預估，點擊率（CTR）預估，轉化率（CVR）預估等。Y 和 Y ? 中的每個元素〖y?u,i〗和 y ?_(u,i)為用戶 u 對商品 i 真實標簽和預測輸出。一般情況下，標簽矩陣 Y 不可能被全部觀測到。樣本被觀測的變量表示為 o_(u,i)∈{0,1}，考慮到無缺失樣本的情況，則的預測不準確度定義為：

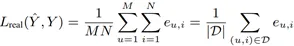
其中，e_(u,i) 為預測誤差。預測問題的目標是最小化上述預測不準確度 L_real。事實上，只有觀測標簽集合 Y^O 能被用于建模。樸素預估方法通過建立模型最小化如下所示的預測不準確度。

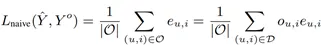
如果每個樣本缺失的概率相同，那么上述的樸素預估方法是無偏的。但是，如果使用的樣本是 MNAR 的，那么上述估計器是有偏的。

考慮到 MNAR 數據帶來的樣本選擇偏差問題，研究人員提出各種無偏估計方法來克服這個問題，如：EIB，IPS/IPW，DR，以及它們的各種變體。EIB、IPS、DR 估計器的損失函數如下所示：

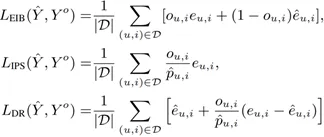
其中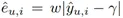，為缺失數據的 MAE 插補誤差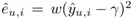，為缺失數據的MSE插補誤差，w 和 γ 為超參數。p ?_(u,i) ?(0,1) 為傾向性分數。對于樸素估計器、EIB、IPW/IPS、DR 方法的偏差和方差公式由下表給出。

其中，，。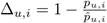

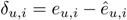通常來說，插補誤差預估模型的學習也涉及到 MNAR 問題。一些聯合學習算法，如 DR-JL 等，使用傾向模型來克服這個問題。因此，傾向性估計在無偏性和穩健性方面具有關鍵作用。此外，很難準確估計所有用戶-物品對的插補誤差，因此很難實現 EIB 估計器的無偏性。如果傾向性估計 p ?_(u,i) 是準確的，即 p ?_(u,i)=p_(u,i)，那么 IPS 和 DR 估計器是無偏的。實際應用中，對于一個新的數據集，我們無法事先知道該數據集中傾向概率的范圍。因此，一個新的數據集可能會引入極小的傾向概率導致 IPS 和 DR 的方差非常大，這將破壞估計器預估性能的穩定性，尤其是對于較大的數據集。這對于實際工業場景是不可接受的。根據表格中給出的各個估計器偏差方差的表達式，傾向性越小，方差越大。當傾向性分數趨于零時，方差趨于無窮大。同樣，其他基于 IPS 和 DR 的無偏估計方法的方差也是無界的。另一方面，雖然在預測誤差 e_(u,i) 是有界時，樸素方法和 EIB 方法的方差是有界的，但要實現無偏估計卻很困難，甚至是不可能的。

正則化技術和靜態估計器的局限性

定義具有正則化的估計器的一般形式為：

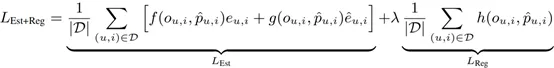
其中，函數 f(?,?)≠0 滿足 f(0,p ?_(u,i) )=0，g(?,?) 和 h(?,?) 是關于 o 和 p ?_(u,i) 的函數。〖L?Est〗和 L_Reg 分別是估計器和正則化器的預測不準確性，對于所有的用戶-商品對，它們滿足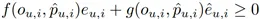和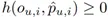。λ>0 為標量權重。上述表達式給出的估計器的一般形式 L_Est 涵蓋了現有的大部分估計器，涉及 EIB、IPS、DR、MRDR、TDR、MIS、IPS/DR-SV 以及其他基于 IPS 和 DR 方法的估計器。另一方面，幾乎所有現有的正則化設計，包括 SV、MIS、BMSE 等正則化方法，都可以轉化為 L_Reg 給出的一般形式。在以前的工作中，正則化技術在一定程度上降低了估計器的方差并改善了泛化性能。然而，它仍然有一些不可避免的局限性（相關理論細節及其證明，參見原論文 3.1 節）：

• 對于具有正則化項的一般估計器 L_(Est+Reg)，在不犧牲無偏性的同時減少方差是不可能的。
• 正則化方法 L_Reg 無法保證估計器方差和泛化誤差是有界的。

根據之前的研究工作和本工作得到的理論結果，正則化技術在一定程度上可以減少方差，但不能使估計器具有有界方差和泛化誤差界。或者說，正則化技術對改善模型預測和泛化性能的影響是有限的。

對于估計器 L_Est，大量的方法追求無偏估計或者追求估計方差的減少，再或者通過手動設計估計器來實現偏差和方差的簡單折衷。本工作我們發現一般形式的估計器存在如下的局限性：

• 對于一般形式的估計器 L_Est，估計器的無偏性將不可避免地導致無界方差和泛化誤差界。

這說明，對于廣義形式的估計器來說，無偏性和有界方差、泛化誤差不可兼得。因此我們認為估計器設計的核心目標不僅僅是消除偏差、減少方差或僅僅實現偏差-方差的簡單折衷，而是關于偏差和方差之間的定量聯合優化，有必要開發一個動態估計框架來實現定量聯合優化，動態估計器能夠從用戶-商品對的維度選擇合適的估計器來實現最小化泛化誤差的目的。

三、細粒度動態框架及估計器設計準則

基于 IPS 和基于 DR 的動態學習框架設計如下：

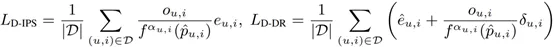
其中，f(?) 為需要設計的函數，α_(u,i)∈[0,1] 為可優化的參數。當 f(p ?_(u,i) )=p ?_(u,i)  且 ?α_(u,i)=1，D-IPS 和 D-DR 分別等價于原始的 IPS 和 DR 估計器，它們具有無偏性。當 f(p ?_(u,i) )=p ?_(u,i)  且 ?α_(u,i)=0，D-IPS 和 D-DR 分別等價 |O|/D L_naive 和 EIB 方法，它們具有有界方差和泛化誤差界。函數 f(p ?_(u,i) ) 實際上是一個關于傾向性分數的映射，f(p ?_(u,i) ) 的設計準則總結如下

• （保序性）f(p ?_(u,i) )>p ?_(u,i) 單調遞增且滿足 f(0)=0，f(1)=1。
• （同階性）lim┬(p ?_(u,i)→0)?〖p ?_(u,i)/f(p ?_(u,i) ) 〗=C，其中 C>0 為正常數。

符合上述設計原則的一些具體函數表達式總結如下表所示。

D-IPS 和 D-DR 估計器的偏差和方差表達式如下所示：

偏差表達式：

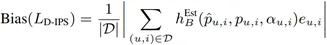
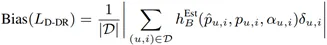
其中，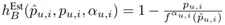

方差表達式：

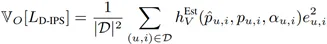
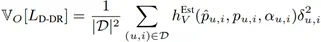
其中，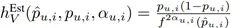

泛化誤差界表達式：

其中，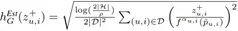

函數 h_B^Est 和 h_V^Est 分別決定了偏差和方差的大小，我們稱函數 h_B^Est 和 h_V^Est 為偏差和方差的決定因子，函數 h_B^Est 和 h_V^Est 曲面如下圖所示，可以看到，h_B^Est 隨著 α_(u,i) 的增大單調遞減；h_V^Est 隨著 α_(u,i) 的增大單調遞增。

四、偏差-方差定量聯合優化

根據函數 h_B^Est 和 h_V^Est 的單調性，偏差-方差的折衷問題可以被定量形式化為如下的聯合優化問題：

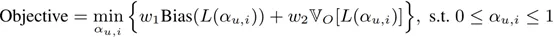
其中，w_1 和 w_2 為偏差和方差的權重。考慮到偏差和方差的決定因子，上述偏差-方差的聯合優化問題可以被轉換為如下所示的優化問題。

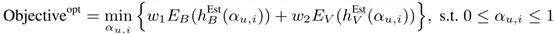
因為 f(p ?_(u,i) ) 的設計準則，所以有 h_B^Est≥0 和 h_V^Est>0。因此，優化問題可以被進一步簡化為：

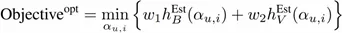
有了這一步的簡化，我們就可以直接得到最優參數的解析解，最優參數的表達式如下所示：

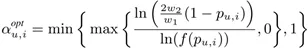
我們通過優化操作可以在不增加計算復雜度的基礎上實現偏差和方差的定量優化，同時從理論層面保證方差和泛化誤差的有界性。

方差和泛化誤差有界性結論

• 如果動態估計器采用 α_(u,i)^opt 作為參數，則對應的方差和泛化誤差是有界的。

五、實驗結果

性能比較

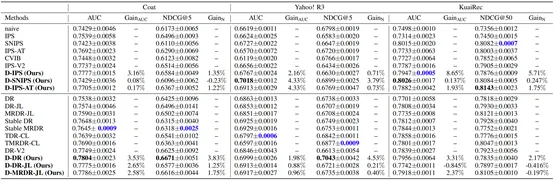
實驗使用了三個具有 MNAR 和 MAR 樣本的現實數據集，分別是 COAT，包含 290 名用戶對 300 件外套的 4,640 個 MAR 和 6,960 個 MNAR 評分；YAHOO! R3，包含 15,400 名用戶對 1,000 首歌曲的 54,000 個 MAR 和 311,704 個 MNAR 評分；以及 KUAIREC，包含 1,411 名用戶對 3,327 個視頻的 4,676,570 條觀看比率記錄。COAT 和 YAHOO! R3 中的評分分數在大于 3 時被二值化為 1，否則為 0。對于 KUAIREC 數據集，觀看率在小于 2 時被二值化為 0，否則為 1。提出的動態估計器和 SOTA 方法的性能對比結果如下表所示。

消融實驗

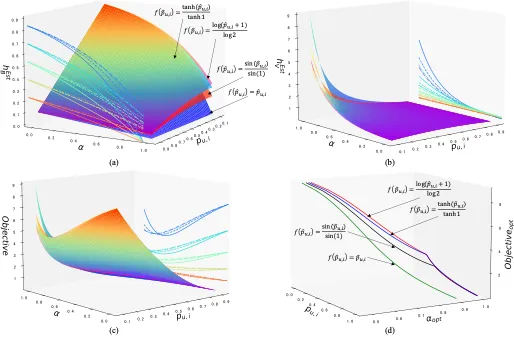
我們通過實驗研究不同權重和函數對動態估計器的影響。我們給出了四個具體的函數表達式。我們將這四個動態估計器的權重設置為 w1=1 和 w2=[0.02, 0.04, 0.06, 0.08, 1]，以研究權重對性能和方差的影響。從最優參數方程可知，最優參數由權重比 w2/w1 決定。因此，我們只關注權重比對估計器性能和方差的影響，不同函數下，不同的權重比的模型性能由下圖給出。

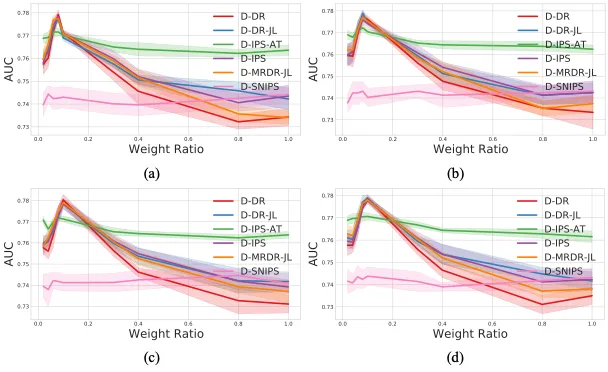
(a)p ?_(u,i)^α; (b) (sin(p ?_(u,i) )/sin?2 )^α; (c) (log?(p ?_(u,i)+1)/log?2 )^α; (d) (tanh?(p ?_(u,i) )/sin?2 )^α

從上圖可以看出，對于 D-IPS、D-IPS-AT、D-DR、D-DR-JL 和 D-MRDR-JL 方法，性能隨著權重比的增加先增加后減小。同時，方差似乎在泛化性能達到最高值時達到最小值。由于權重比越小，動態估計器的偏差越小，上圖中的實驗結果表明，估計器的無偏性并不完全等價于模型性能。實際上，從給出的泛化誤差表達式來看，偏差-方差聯合優化可以最小化估計器的泛化誤差界，從而進一步提高模型的泛化性能。對于 SNIPS，方差減少的特性可能會導致非直觀的性能和方差趨勢。

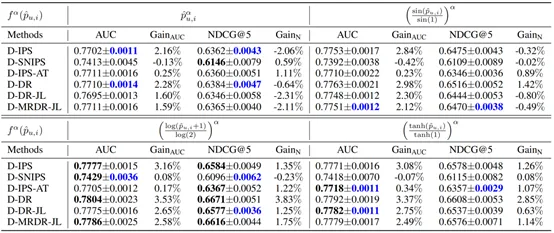
在相同的權重比 w2/w1=0.1 下，我們進一步討論不同函數對模型性能和方差的效果。從下表可以看出幾乎所有具有不同函數表達式的動態估計器性能都優于相應的原始糾偏方法。這進一步證明了所提出的動態學習機制可以極大地提高原始估計器的性能。

六、結語

據我們所知，這是第一個揭示估計器設計本質的工作。該工作指出，估計器設計的本質不僅僅是消除偏差、降低方差或實現簡單的偏差-方差權衡，而是同時定量優化偏差和方差。此外，該工作還闡述了通用正則化技術和靜態估計器的局限性。基于偏差和方差之間關系的一般規律，我們提出了一種系統的動態學習框架，通過細粒度的偏差-方差聯合優化方案，保證了方差和泛化誤差界的有界性。大量的實驗結果驗證了該工作的理論結果和當前動態估計器的性能。在動態估計框架中，對目標函數中權重的搜索以及函數的搜索仍然是一個開放問題，值得進一步探索。