推理的深度邊界:神經網絡如何在有限參數下實現多步推理?

大家好,我是肆〇柒。今天要和大家分享的這項突破性研究來自MBZUAI(穆罕默德·本·扎耶德人工智能大學)、莫斯科物理技術學院神經網絡與深度學習實驗室、莫斯科人工智能研究院以及倫敦數學科學研究所的聯合團隊。這項研究通過精心設計的1dCA基準,首次清晰地區分了模型的規則抽象能力和多步狀態傳播能力,為我們理解神經網絡的"思考"機制提供了新視角。(本文比較晦澀,慎入。如果你覺得晦澀,依然想繼續閱讀,可以直接拉到文末看總結)
當大型語言模型在學術競賽中取得突破性進展時,整個AI界為之震動。像OpenAI的o1和DeepSeek R1模型在2024年美國數學奧林匹克競賽資格賽(AIME)中獲得了前500名的排名,這一成績足以讓它們進入正式的美國數學奧林匹克競賽(USAMO)。更令人驚嘆的是,OpenAI的系統在國際信息學奧林匹克競賽(IOI 2025)中取得了第6名的優異成績。與此同時,Google DeepMind和OpenAI的系統在國際數學奧林匹克競賽(IMO 2025)中均達到了金牌標準,實現了AI在頂級學術競賽中的里程碑式突破。
然而,在歡呼之余,一個更深層、更本質的問題也隨之浮現:這些令人興奮的表現,究竟是源于模型對海量數據的"記憶"與模式匹配,還是它們確實掌握了人類引以為傲的、循序漸進的"多步推理"能力?
研究表明,當前的LLM,更像是一位擅長"看一步走一步"的棋手,而非能深思熟慮、推演數步的宗師。它的"推理"能力,可能在第一步之后就戛然而止。《Beyond Memorization: Extending Reasoning Depth with Recurrence, Memory and Test-Time Compute Scaling》這篇研究,通過一個精巧的"思想實驗",給出了一個顛覆性的答案:多步狀態傳播是真正的推理瓶頸,而固定深度是難以逾越的硬約束。這項研究不僅揭示了LLM"思考"的邊界,更為我們指明了突破這一邊界的具體路徑。
一維細胞自動機:神經網絡推理能力的"試金石"
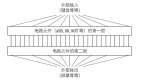
要理解這項研究,首先需要了解"一維細胞自動機"(1dCA)這一核心工具。現在想象一排20個燈泡(論文中W=20),每個燈泡只能是亮(1)或滅(0)。這排燈泡就是一維細胞自動機的"狀態"。
現在,設定一個簡單規則:每個燈泡下一秒的狀態,取決于它自己和左右各2個鄰居(共5個燈泡)當前的狀態。這個規則可以用一個32位的字符串表示(因為5個二進制輸入有2?=32種可能組合)。
例如,如果規則字符串是"01011111100100000101111011111100":
- 當5個輸入是"00000"時,輸出是規則字符串的第0位(即"0")
- 當5個輸入是"00001"時,輸出是規則字符串的第1位(即"1")
- 以此類推...
從一個初始狀態(如"10110111001000110100")開始,反復應用這個規則,就會產生一個隨時間演化的狀態序列,稱為"軌道"(orbit)。

一維細胞自動機示意圖:5位窗口決定下一個狀態
打造"純凈"的推理試驗場——1dCA基準
為什么是細胞自動機?
要研究"純粹"的推理,首先需要一個能完美模擬推理本質的試驗場。一維細胞自動機(1dCA)因其簡潔而強大的特性,成為了理想之選。在一個1dCA系統中,全局狀態由一排二進制細胞構成,其演化完全由一個局部的布爾規則  決定。給定一個初始狀態,系統會生成一條確定的演化軌跡(Orbit)。
決定。給定一個初始狀態,系統會生成一條確定的演化軌跡(Orbit)。
這個過程天然地映射了人類推理的兩個核心階段:

為什么這個設計很巧妙?
研究者通過一個關鍵創新確保了任何觀察到的成功都反映了模型對規則的泛化能力,而非簡單的數據查找:訓練集和測試集所使用的局部規則是完全不重疊的隨機集合。這意味著,模型在測試時遇到的每一個規則都是全新的,其成功與否,完全取決于它是否在訓練過程中學會了通用的"推理算法"。這種設計將"記憶"的干擾徹底剝離,讓我們能清晰地觀察到模型真正的推理能力。


一維細胞自動機的學習 (a) 用局部規則更新狀態 (b) 1dCA 的“軌道”是一串長度為 W = 20 的二進制字符串序列;最前面 k = 10 個狀態(紅色框標出)被編碼為 Transformer 的輸入 (c) 給定軌道的一部分,模型學習預測下一個狀態(簡稱 O-S)
在此基礎上,研究者定義了"推理深度"k,即模型需要預測從當前狀態起第 k 步之后的狀態。為了全面評估模型能力,他們設計了四種任務變體:

這個精心設計的基準,為后續的架構大比拼和策略分析奠定了堅實、可控且無偏的基礎,讓我們得以在"純凈"的環境中,觀察模型推理能力的真相。
基礎架構大比拼——效率與深度的殘酷現實
在公平的競技場上,研究者將四種主流架構——Transformer (GPTNeox)、LSTM、狀態空間模型 (Mamba) 和關聯循環記憶Transformer (ARMT)——置于相同的起跑線:統一使用僅有4層、128維的小型模型。這一設置至關重要,它確保了所有比較都是在固定參數預算下進行的,從而能真實反映出不同架構在效率上的優劣。
實驗結果揭示了一個殘酷而清晰的現實:單步推理易如反掌,多步推理難如登天。

單步準確率近乎完美,但多步性能崩潰
這張圖是整個研究的判決書。它宣告了絕大多數神經網絡的"死刑":在單步預測 (k=1) 上,準確率普遍超過95%(LSTM略低,約90%),這證明模型確實學會了從軌跡中抽象出底層規則,完成了第一階段的推理。然而,一旦任務要求預測兩步之后的狀態 (k=2),除了ARMT之外,其他所有模型的準確率都像自由落體一樣暴跌至25%以下。這場"斷崖式下跌"無情地揭示了一個事實:模型或許"懂"了規則,卻完全喪失了應用規則進行連續推演的能力。更令人深思的是O-RS任務的結果。

規則預測的高準確率無法轉化為多步預測能力
研究者本以為,通過要求模型同時輸出規則,直接強化"規則推斷"的監督信號,能"手把手"地教會模型如何進行規則推斷,從而為多步推理打好基礎。但結果卻顯示,這種直接的監督對提升 k>1 的性能幾乎無效。這個"意外"是研究的關鍵轉折點,它將研究者的目光從"規則推斷"徹底轉向了"狀態傳播",揭示出后者才是阻礙模型進行深度推理的真正"攔路虎"。那么,如何突破這個瓶頸?增加模型容量是否有效?研究者通過對比實驗給出了明確答案:深度 > 寬度。

深度擴展顯著提升多步預測能力
增加Transformer的層數(縱向深度擴展)能顯著提升其在 k=2,3 時的表現。例如,從4層增加到6層,k=2 的準確率從約40%躍升至80%以上;增加到12層,k=3 的準確率也能提升至約60%。相比之下,單純增加模型的寬度(dmodel)帶來的收益則微乎其微。

寬度擴展對多步推理收效甚微
當 dmodel 從64增加到128時,性能有小幅提升,但繼續增加到256或512,收益幾乎可以忽略不計。綜上,實驗數據清晰地指向一個核心結論:狀態傳播是比規則推斷更深的瓶頸,而突破此瓶頸的根本在于增加模型的縱向深度。

然而上圖圖(a)也揭示了一個嚴峻的工程現實:為每個額外的推理步驟都堆疊一層新網絡,其成本是線性增長且不可持續的。這自然引出了一個關鍵的研究命題:我們能否在不增加任何靜態參數的前提下,讓一個4層的"小"模型,完成6層甚至8層模型才能勝任的多步推理任務? 帶著這個問題,我們繼續向后看,探索循環、動態計算與強化學習等"四兩撥千斤"的高效策略。
突破瓶頸——如何在不增加參數的前提下擴展"有效推理深度"?
面對固定深度的硬性約束,研究者探索了四種截然不同的策略,每一種都在效率與性能之間做出了獨特的權衡。
策略一:引入"循環"架構 (Recurrence) —— ARMT的效率勝利
ARMT(Associative Recurrent Memory Transformer)是這場效率競賽中的首個贏家。它通過在Transformer架構中引入分段級別的循環和關聯記憶,強制模型在處理不同片段時復用和傳遞信息。具體實現上,輸入序列被分割成多個片段(例如,每兩個連續狀態為一個片段),ARMT在處理完一個片段后,會將其輸出的記憶狀態傳遞給下一個片段作為輸入。

ACT顯著提升Transformer類模型的多步預測能力
實驗結果顯示,ARMT是唯一一個能在4層架構下穩定處理 k=2 任務的基礎模型(準確率約43%),而其他4層模型在此任務上的準確率均低于25%。
為什么ARMT能成功? 關鍵在于其架構設計強制模型分離規則與狀態表示。這種分離使ARMT能夠生成一個中間狀態的隱藏表示,然后應用規則進行預測,從而在不增加任何靜態參數的前提下,動態地擴展了模型的"有效深度"。這是一種典型的參數高效方案,證明了循環機制在克服狀態傳播瓶頸上的獨特優勢。然而,其能力也受限于"分段"設計,無法突破 k=2 的上限,表明單純的架構循環有其固有的邊界。
策略二:動態"思考時間" (Adaptive Computation Time - ACT) —— 計算效率的優雅方案

為標準的Transformer(GPTNeox)添加ACT后,其性能在 k=2 時獲得了穩定提升(從40%提升至約60%),相當于獲得了約"+1步"的有效深度。ACT的精妙之處在于:它通過在測試時動態增加計算量(而非在訓練時增加參數量)來換取性能提升,實現了計算高效的深度擴展。進一步的消融實驗(FCT vs ACT)

固定計算步數(FCT)與自適應計算時間(ACT)在Orbit-State任務中的比較
揭示了一個關鍵洞察:ACT的"自適應性"是其價值所在。研究者設置了一個"固定計算步數"(FCT)的基線,強制模型每次都進行3步計算(這是ACT實驗中觀察到的平均上限)。結果顯示,在O-S任務上,FCT與ACT表現相當,但在更復雜的-O任務上,ACT明顯優于FCT。

固定計算步數(FCT)在Orbit-Orbit任務中表現不佳
這說明ACT的智能之處在于它能"按需分配"計算資源,避免在簡單樣本上浪費算力,從而在整體上實現更優的效率-性能平衡。
策略三:強化學習"自省" (GRPO) —— 無監督擴展深度的革命性突破
如果說前兩種策略是"工程師"的智慧,那么GRPO(Group Relative Policy Optimization)則展現了"進化論"的力量。在完全沒有中間步驟監督的情況下,研究者僅通過最終答案的正確與否作為獎勵信號,利用強化學習訓練模型。

無監督RL訓練使模型推理深度擴展至k=3
結果令人震驚:模型學會了在輸出最終答案前,自回歸地生成一系列內部的"思考"Token。通過這種方式,它成功地將推理深度擴展到了 k=3,其性能(約40%)甚至可以媲美有監督情況下的 k=2 任務。
這一發現為何具有革命性意義? 它挑戰了"顯式中間表示是深度推理唯一可靠途徑"的固有認知,證明了模型可以在無監督的條件下,自發地學會"內部思考"以增加推理深度。僅憑最終答案的獎勵信號,就足以引導模型發展出復雜的、多步的內部推理過程,為未來無監督、自適應的推理能力涌現開辟了全新的道路。這表明,推理能力的涌現可能不需要人類精心設計的CoT提示,而是可以通過簡單的獎勵機制自然演化出來。
策略四:鏈式思維監督 (Chain-of-Thought - CoT) —— 可靠但昂貴的終極方案
當有充足的中間步驟監督信號時,CoT(Chain-of-Thought)訓練展現出了無與倫比的可靠性。

CoT方法在有監督情況下顯著優于基于深度的ACT方法
在這種范式下,復雜的多步預測任務被分解為一系列簡單的自回歸單步生成任務。無論是GPTNeox還是ARMT,經過CoT訓練后,都能在 k=4 的任務上達到接近100%的準確率。這無可辯駁地證明了,對"狀態傳播"過程的直接監督,是實現深度泛化的最可靠途徑。
然而,這種可靠性是有代價的: 它依賴于昂貴且難以獲取的中間步驟標注數據,并且在推理時會生成大量額外的Token,帶來顯著的計算開銷,是一種"重裝上陣"的解決方案。值得注意的是,單純使用O-O任務(即并行預測所有中間狀態)進行訓練,效果并不理想,其性能甚至低于O-S任務。只有當O-O與ACT結合,或者升級為真正的、自回歸的CoT訓練時,性能才得到質的飛躍。這表明,順序推理比并行推理更能有效模擬人類的思考過程。
超越語言——在群乘法任務上的普適性驗證
為了驗證上述發現在更廣泛場景下的普適性,研究者在"群乘法"基準上進行了補充實驗。之所以選擇這個基準,是因為其計算本質與1dCA高度相似:都需要模型在內部維護一個"狀態"(當前累積乘積),并根據輸入序列中的新元素,按特定"規則"(群運算)反復更新這個狀態。 這種同構性,使得我們可以將"序列長度"直接類比為1dCA中的"推理深度k",從而在一個完全不同的任務上,復現并驗證關于模型深度、循環和動態計算的核心發現。
該任務要求模型計算一個序列中所有元素的累積乘積,其計算復雜度隨序列長度(即推理深度)線性增長。實驗結果與1dCA基準高度一致。

ACT顯著降低模型解決群乘法任務所需的深度
Transformer和Mamba這類被理論證明為"TC0-limited"的模型,需要隨著任務長度(深度)的增加而線性增加其層數,才能維持70%以上的準確率。相比之下,ARMT和LSTM憑借其內在的循環特性,能夠以恒定的層數(僅需1-2層)解決任意深度的任務,再次彰顯了循環架構在參數效率上的巨大優勢。
更引人注目的是,為Transformer添加ACT,也能顯著降低其所需的層數,部分緩解了深度瓶頸,這進一步證明了動態計算策略的廣泛適用性和價值。例如,在A5群上處理長度為40的序列,標準Transformer可能需要8層以上,而添加ACT后,4層即可勝任。這一結果與1dCA基準中的發現完美呼應,證實了這些策略在不同任務中的普適性。
效率、架構與訓練
現在,讓我們回到最初的問題:神經網絡如何真正"推理"?這項研究給出了清晰而深刻的答案。
首先,論文明確區分了推理的兩個本質階段:規則抽象與多步狀態傳播。 在1dCA基準中,所有模型都能高效完成規則抽象(k=1時準確率>95%),但當需要多步狀態傳播(k≥2)時,大多數模型性能急劇下降。這表明,規則抽象相對容易,而多步狀態傳播才是真正的瓶頸。正如論文中所說:"規則抽象可以從有限觀察中完成,但狀態傳播需要模型在內部維護和更新中間狀態,這是一個更復雜的計算過程。"
其次,論文揭示了模型深度與寬度對推理能力的不同影響。 在神經網絡中,寬度指每層神經元數量(d_model),深度指網絡層數。

上圖顯示,增加寬度對多步推理能力的提升有限,特別是在達到128維度后,繼續增加寬度收益甚微。而下圖則顯示,增加深度能顯著提升多步推理能力:從4層增加到6層,k=2的準確率從約40%躍升至80%以上;增加到12層,k=3的準確率也能提升至約60%。

所以:推理能力不僅與模型寬度相關,層數的深度更為關鍵,特別是在需要多步推理的任務中。
第三,論文證明了"固定深度是難以逾越的硬約束"。 一個4層的模型,即使在單步推理上表現完美,也難以可靠地完成兩步以上的推理。這解釋了為什么LLM在奧賽中表現優異——這些任務往往可以被分解為一系列單步決策,而非真正需要多步規劃的復雜問題。
那么,如何突破這一硬約束?論文提出了三種高效策略:
1. 循環架構(如ARMT):通過分段級別的循環,強制模型分離規則與狀態表示,使4層模型能處理k=2任務。這是一種參數高效的方案,因為它在不增加靜態參數的情況下擴展了有效深度。
2. 動態計算(如ACT):通過測試時的自適應計算,為Transformer等模型提供約"+1步"的額外推理能力。這是一種計算高效的方案,因為它只在需要時才增加計算量。
3. 無監督強化學習(如GRPO):讓模型通過強化學習自發生成"思考"Token,將推理深度擴展到k=3。這是最具革命性的發現,因為它證明了模型可以在沒有中間監督的情況下學會"內部思考"。
最后,論文指出,有監督的鏈式思維(CoT)是目前最可靠的深度推理方案,但它需要昂貴的標注成本和計算開銷。 當有中間步驟監督時,模型能輕松達到k=4的近100%準確率,這再次證明了顯式中間表示對深度推理的關鍵作用。
再總結一下,這項研究告訴我們:
- 神經網絡的"推理"能力有其根本限制,主要體現在多步狀態傳播上
- 固定深度是難以逾越的硬約束,增加寬度效果有限,增加深度有效但成本高昂
- 循環、動態計算和強化學習提供了在不增加參數前提下擴展有效推理深度的高效路徑
- 規則抽象相對容易,但多步狀態傳播才是真正挑戰,也是未來研究的關鍵方向
LLM的"思考"不應是一個黑箱。 這項研究為我們提供了一把精密的"解剖刀"——1dCA基準,它讓我們得以清晰地看到:真正的深度推理,是"規則抽象"與"狀態傳播"的雙重作用,而后者往往是無聲的瓶頸。 通往"深思熟慮"的AI之路,不是無休止地堆砌參數,而要如何用循環的巧思、動態的智慧和訓練的魔法,在有限的"腦容量"內,激發出無限的"思考深度"。
回到文章開頭的那個問題:LLM在奧賽上的勝利,是真正的推理嗎?基于1dCA基準的研究給出的答案是復雜的。在單步決策上,它們無疑是大師級的。但在需要多步規劃、狀態追蹤的深層推理上,它們的表現急劇衰減,除非我們人為地為其增加深度、引入循環或提供詳細的中間指導。
最終的勝利,將屬于那些能在架構的巧思、訓練的智慧與計算的效率之間,找到完美平衡點的探索者。 因為推理時,深度不是目的,而是手段;效率才是通往真正智能的橋梁。正如1dCA基準所示范的,未來研究應設計能明確分離"規則推斷"與"多步狀態傳播"的可控實驗環境,以精準定位模型瓶頸。研究者應系統性地報告模型在不同推理深度(k=1,2,3,4...)下的表現,并注明所使用的模型參數量和計算開銷,以全面評估其有效推理深度與效率。
自適應計算策略(如ACT)和無監督的推理擴展方法(如GRPO)是極具前景的Scaling方向,值得深入探索。畢竟,真正的智能不在于記住答案,而在于學會思考——即使在資源有限的條件下,也能找到通往答案的路徑。