深度強化學習在機器人控制 、自動駕駛等復雜決策任務中取得了巨大成功([2])。

然而，傳統強化學習算法訓練出的策略網絡往往對觀測噪聲和外部擾動十分敏感，導致輸出的動作信號缺乏平滑性([3-5])。

現有的平滑方法大多從時域入手，例如設計與任務高度耦合的獎勵函數、對網絡施加復雜的正則化約束、或構建分層策略等。

這些方法雖然在特定任務上有效，但往往存在泛化性不強、限制網絡表達能力或設計復雜等問題。

清華大學智能駕駛課題組（iDLab）另辟蹊徑，在智能車輛領域頂級期刊IEEE Transactions on Intelligent Vehicles上發表的最新研究成果指出：控制策略的不平滑現象，本質上是輸出序列中高頻分量導致的。

圖片

論文鏈接：https://ieeexplore.ieee.org/document/10643291

這些高頻分量主要由觀測噪聲引入，并在網絡的正向傳播中被放大。

因此，如果能設計一個神經網絡，使其自身具備低通濾波能力，在濾除無用高頻噪聲的同時保留對控制有益的低頻信號，即可有效提升策略的平滑性與魯棒性。

為實現上述目標，研究團隊設計了名為Smonet的新型神經網絡架構。

其核心是一個由多個串聯濾波層組成的濾波模塊，該網絡包含三大關鍵組件：

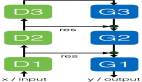
圖1 Smonet網絡架構

1. 慣性濾波單元 (Inertia Cell)

該單元是實現低通濾波的核心。它基于簡單高效的一階慣性濾波過程，通過對輸入信號進行帶有指數衰減權重的積分，有效濾除高頻噪聲成分，從而學習到一個平滑、低頻的隱藏狀態表征。

2. 自適應調節單元 (Adaptive Cell)

濾波不可避免地會引入延遲，過度平滑可能導致系統在需要快速響應時表現不佳。為解決這一矛盾，Smonet在每個濾波層中都設計了一個自適應單元。該單元能夠根據當前輸入信號的動態特性，自適應地調整慣性單元的濾波強度。這使得Smonet能夠在系統狀態平穩時提供強力平滑，在需要緊急規避或跟蹤突變信號時又能實現快速響應，達到了平滑性與性能的有效平衡。

圖2 Smonet濾波層

3. Smonet正則化訓練方法

僅有網絡結構還不夠，為引導Smonet的濾波能力向「最優」的方向學習，研究團隊進一步提出了一種配套的正則化訓練方法。

該方法通過在標準強化學習策略損失函數中引入一個與濾波因子相關的正則項，鼓勵網絡在大部分狀態下采用較小的濾波因子(即更強的平滑能力，同時允許策略的性能優化目標在必要時「推高」濾波因子以保證快速響應。

這種設計在優化過程中實現了控制性能和平滑性之間的動態權衡。

實驗結果

研究團隊在多個Mujoco仿真機器人控制任務和一個真實世界的移動機器人避障實驗中，對Smonet的性能進行了全面驗證。

仿真機器人控制

在Humanoid、Ant等多個標準測試環境中，Smonet與傳統MLP、GRU網絡進行了對比。

噪聲魯棒性：在無噪聲環境下，Smonet的控制性能與其余網絡結構相當。但在引入高斯噪聲后，MLP和GRU的性能顯著下降，而Smonet得益于其濾波能力，依然能保持高水平的控制性能。

動作平滑性：在所有噪聲水平下，Smonet的動作波動率和平均加權頻率均顯著低于對比方法。與MLP相比，平均降幅分別達到48.2%和32.1%。

圖4 不同噪聲水平下的動作平滑性指標對比

移動機器人避障

為了驗證Smonet在真實世界中的效果，研究團隊將訓練好的策略部署到一臺兩輪移動機器人上，執行軌跡跟蹤與動態避障任務 。

實驗結果表明，Smonet生成的控制指令明顯比MLP和GRU更平滑、抖動更小。

在引入額外的人工觀測噪聲后，Smonet不僅保持了最低的動作波動，還實現了最低的累積跟蹤誤差，展現出較好的魯棒性。

在高噪聲下，其動作波動率相比MLP和GRU分別降低了57.9%和70.4%。

圖5 真實機器人實驗中的控制動作（左）與累積跟蹤誤差（右）

總結

研究人員針對強化學習在真實世界應用中的動作震蕩痛點，創新性地從頻域視角出發，提出了具備低通濾波能力的神經網絡Smonet。

通過內置的慣性濾波單元、自適應調節單元以及配套的正則化訓練方法，Smonet在不犧牲控制性能的前提下，顯著提升了策略的平滑性和噪聲魯棒性。

仿真與真實世界實驗的成功驗證，證明了該方法在邁向更安全、更穩定、更可靠的智能控制系統方面具有巨大潛力，為強化學習和具身智能技術在現實世界的落地應用鋪平了道路。

參考資料

[1] W. Wang, J. Duan, X. Song, et al. "Smooth Filtering Neural Network for Reinforcement Learning." IEEE Transactions on Intelligent Vehicles, vol. 10, no. 5. pp. 3103-3112, May 2025. 

[2] S. E. Li. Reinforcement Learning for Sequential Decision and Optimal Control. Singapore: Springer Verlag, 2023. 

[3] Y. Wang, W. Wang, X. Song, et al. "ODE-based Smoothing Neural Network for Reinforcement Learning Tasks." The Thirteenth International Conference on Learning Representations (ICLR), 2025. 

[4] X. Song, L. Chen, T. Liu, et al. "LipsNet++: Unifying Filter and Controller into a Policy Network." International Conference on Machine Learning (ICML). PMLR, 2025. 

[5] X. Song, J. Duan, W. Wang, et al. "LipsNet: A Smooth and Robust Neural Network with Adaptive Lipschitz Constant for High Accuracy Optimal Control." International Conference on Machine Learning (ICML). PMLR, 2023.